
En muchos foros se repite, a modo de mantra, que la falta de conservación de nuestras carreteras (y calles, en el caso de las ciudades) se debe fundamentalmente a un problema de orden económico. Por algún u otro motivo (crisis económica, dificultad en aprobar presupuestos, falta de voluntad política, etc.), la falta aparente de recursos obliga a realizar una conservación correctiva o reactiva de las carreteras que, como ya se justificó en un artículo anterior, provoca estados subóptimos en la infraestructura y tiene como consecuencia el incremento del riesgo de accidentes, la reducción de la velocidad de los vehículos, las restricciones de paso y la elección por los usuarios de itinerarios alternativos con mayor tiempo de recorrido. Conviene insistir en este punto, una conservación deficiente genera mayores costes a los usuarios relacionados con el valor del tiempo de viaje, con el vehículo y con los accidentes de tráfico. La justificación económica de las restricciones presupuestarias queda en entredicho cuando se consideran los costes totales del transporte.
Sin embargo, en nuestro grupo de investigación hemos desarrollado modelos que, incluso en el caso de disponer presupuestos restrictivos, pueden maximizar el estado o condición, no de una carretera, sino de una red completa, considerando, además, distintas funciones objetivo (costes económicos, sociales y medioambientales). Pero para entender mejor el problema, expongo a continuación la dificultad intrínseca de este tipo de problemas y justificaré las razones por las que muchos gestores del mantenimiento de carreteras toman decisiones que se alejan de ser óptimas.
La clave para entender la magnitud del problema radica en la dificultad que tienen los gestores de la red de carreteras en la toma de decisiones debido a la explosión combinatoria de las soluciones posibles cuando se tienen en cuenta distintos tipos de tratamientos de preservación, mantenimiento y rehabilitación (P+M+R) y los periodos de aplicación. Dicho de otra forma, en una red de carreteras se trata de decidir en qué tramo de la red se aplica un tratamiento de los múltiples posibles y cuándo se debe realizar. Las decisiones tomadas conforman el programa de conservación de la red de carreteras.
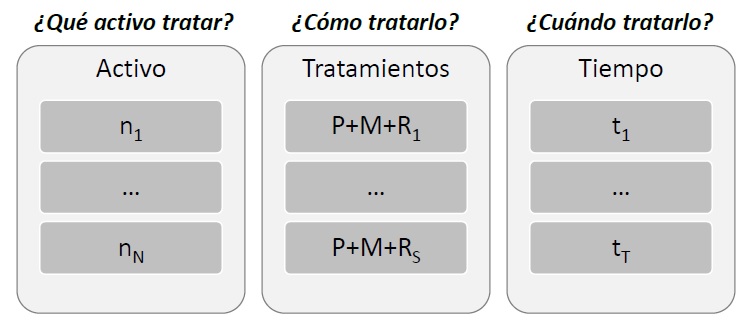
En la Figura 2 se representan las variables fundamentales que conforman el problema. En una red de carreteras tenemos N activos (tramos considerados), S posibles tratamientos, cada uno de los cuales se aplicará en el instante t en los T años considerados en el programa de conservación.
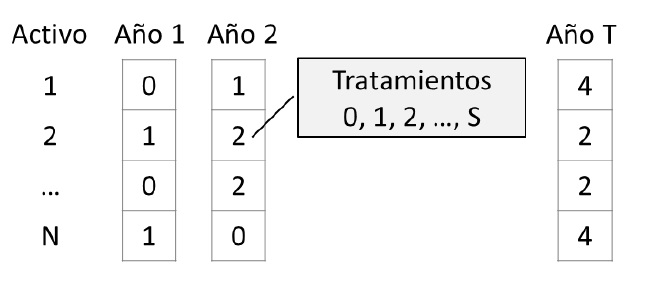
El programa de conservación resultante de las decisiones tomadas para un horizonte de T años nos dirá para cada uno de los años dónde actuar y qué tipo de tratamiento se deberá efectuar. En la Figura 3 queda representada un posible programa fruto de las decisiones tomadas.
Lo difícil de este problema, como hemos dicho anteriormente, es acertar con el mejor programa de conservación. No hay más remedio que aplicar técnicas de optimización para resolver el problema si los presupuestos son escasos. Caben dos enfoques, el secuencial y el holístico. El primero se centra en un activo (tramo de carretera, calle en una ciudad) y se decide qué tratamientos y cuándo se van a aplicar. En este caso el problema tiene N·S^T soluciones. En cambio, el enfoque holístico considera toda la red: se trata de elegir qué activo tiene prioridad en la red y luego decidir qué tratamiento y cuándo se aplica. Aquí se dispara el número de posibles soluciones a S^(N·T). A modo de ejemplo, teniendo en cuenta solo dos tratamientos (S=2), un horizonte de 10 años (T=10) y 7 tramos diferentes de carretera (N=7), el número de posibles soluciones es de 1,18E+21.
La única forma de abordar este problema es con algoritmos heurísticos de optimización multiobjetivo. Os dejo algunas referencias de cómo hemos resuelto en nuestro grupo de investigación este problema y en un artículo posterior os explico cómo formular el problema de optimización (funciones objetivo, restricciones, etc.). Como ya dije en artículos anteriores, la puerta está abierta a quien quiera participar en nuestro grupo.
Referencias:
- SALAS, J.; YEPES, V. (2019). MS-ReRO and D-ROSE methods: assessing relational uncertainty and evaluating scenarios’ risks and opportunities on multi-scale infrastructure systems. Journal of Cleaner Production, (accepted, in press).
- SIERRA, L.A.; PELLICER, E.; YEPES, V. (2017). Method for estimating the social sustainability of infrastructure projects. Environmental Impact Assessment Review, 65:41-53.
- SIERRA, L.A.; YEPES, V.; GARCÍA-SEGURA, T.; PELLICER, E. (2018). Bayesian network method for decision-making about the social sustainability of infrastructure projects. Journal of Cleaner Production, 176:521-534.
- SIERRA, L.A.; YEPES, V.; PELLICER, E. (2017). Assessing the social sustainability contribution of an infrastructure project under conditions of uncertainty. Environmental Impact Assessment Review, 67:61-72.
- SIERRA, L.A.; YEPES, V.; PELLICER, E. (2018). A review of multi-criteria assessment of the social sustainability of infrastructures. Journal of Cleaner Production, 187:496-513.
- TORRES-MACHÍ, C. (2015). Optimización heurística multiobjetivo para la gestión de activos de infraestructuras de transporte terrestre. Tesis doctoral. Universitat Politècnica de València – Pontificia Universidad Católica de Chile.
- TORRES-MACHÍ, C.; CHAMORRO, A.; PELLICER, E.; YEPES, V.; VIDELA, C. (2015). Sustainable pavement management: Integrating economic, technical, and environmental aspects in decision making. Transportation Research Record, 2523:56-63.
- TORRES-MACHÍ, C.; CHAMORRO, A.; VIDELA, C.; PELLICER, E.; YEPES, V. (2014). An iterative approach for the optimization of pavement maintenance management at the network level. The Scientific World Journal, Volume 2014, Article ID 524329, 11 pages.
- TORRES-MACHÍ, C.; CHAMORRO, A.; YEPES, V.; PELLICER, E. (2014). Current models and practices of economic and environmental evaluation for sustainable network-level pavement management. Revista de la Construcción, 13(2): 49-56.
- TORRES-MACHI, C.; PELLICER, E.; YEPES, V.; CHAMORRO, A. (2017). Towards a sustainable optimization of pavement maintenance programs under budgetary restrictions. Journal of Cleaner Production, 148:90-102.
- YEPES, V.; TORRES-MACHÍ, C.; CHAMORRO, A.; PELLICER, E. (2016). Optimal pavement maintenance programs based on a hybrid greedy randomized adaptive search procedure algorithm. Journal of Civil Engineering and Management, 22(4):540-550.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
