Introducción: El arte perdido del cálculo visual.
Introducción: El arte perdido del cálculo visual.
Vivimos en un mundo donde cualquier cálculo, por complejo que sea, está a un clic de distancia. Dependemos totalmente de las calculadoras digitales y las computadoras, hasta el punto de que resulta difícil imaginar cómo se resolvían problemas de ingeniería complejos antes de la era digital. Sin embargo, hubo una herramienta ingeniosa y puramente visual que dominó el mundo técnico durante décadas: el nomograma.
¿Cómo es posible que una tecnología del siglo XVII, considerada obsoleta durante más de cuarenta años, esté resurgiendo en campos de alta tecnología como la ingeniería minera? La respuesta se halla en una sorprendente sinergia entre la sabiduría analógica del pasado y el poder del código abierto actual.
1. Más allá de la nostalgia: una herramienta antigua para problemas modernos.
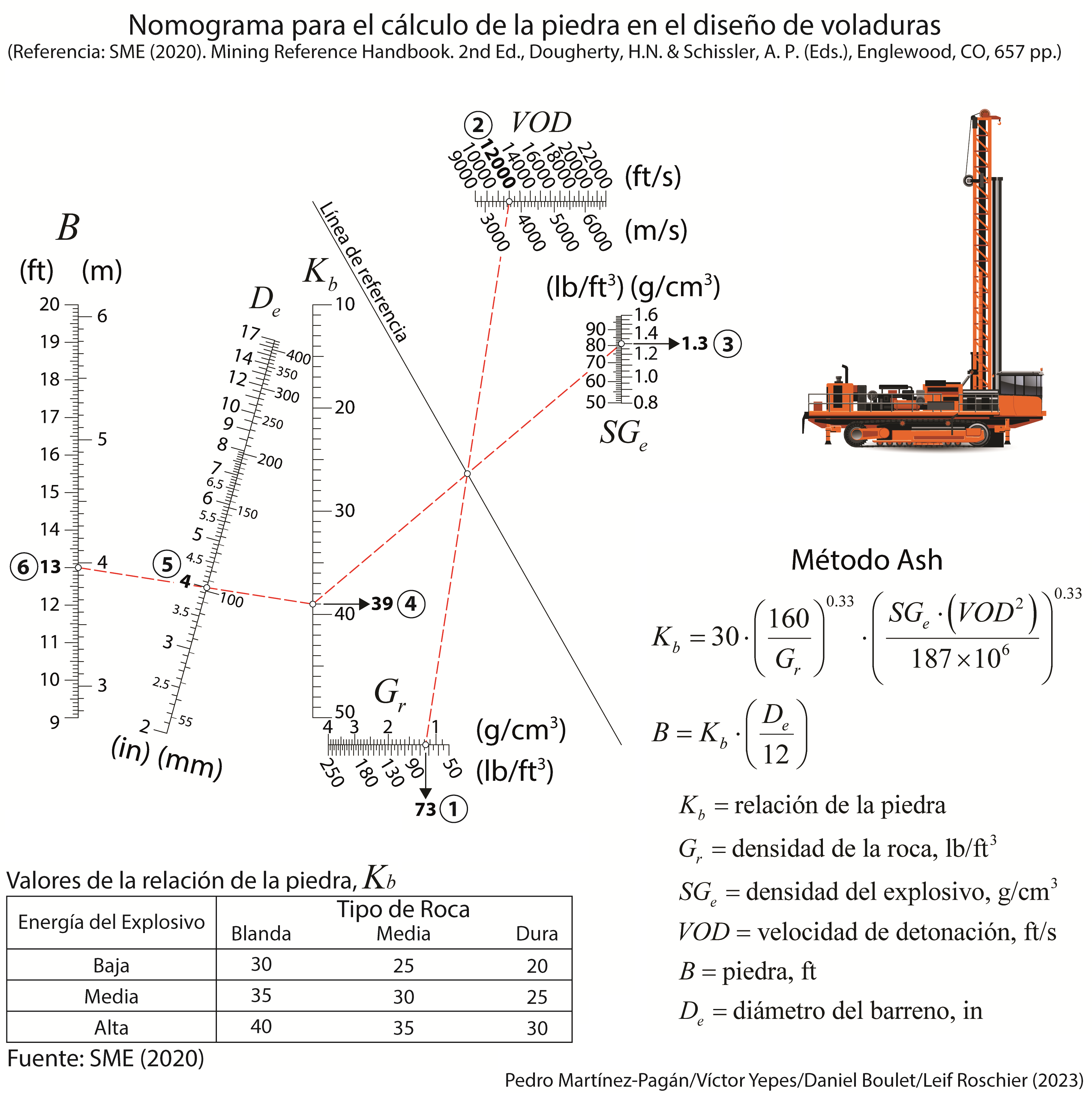
Un nomograma es una representación gráfica de una ecuación matemática. Está compuesto por una serie de ejes graduados, rectos o curvos, que representan las variables de la fórmula. Para resolver la ecuación, basta con trazar una línea recta (llamada isopleta) que conecte los valores conocidos en sus respectivos ejes; el punto en el que esta línea corta el eje de la variable desconocida proporciona la solución al instante.
Aunque sus orígenes se remontan al siglo XVII, los nomogramas se convirtieron en herramientas indispensables en el siglo XIX para la navegación astronómica y, más tarde, en la década de 1920, para resolver complejos cálculos de ingeniería relacionados con la presión, el volumen y la temperatura. Durante el resto del siglo XX, vivieron su época dorada en campos como la medicina, la aeronáutica y la química, pero la llegada de los ordenadores en la década de 1980 los dejó relegados al olvido. Hoy, contra todo pronóstico, están volviendo a ser útiles, no como una curiosidad histórica, sino como una herramienta práctica y potente, especialmente en entornos de campo o talleres donde la tecnología digital no siempre es la mejor opción.
2. Ingeniería para todos: resuelve fórmulas complejas solo con una regla.
El beneficio más destacado de los nomogramas es su capacidad para democratizar el cálculo. Permiten que cualquier persona, independientemente de su formación matemática, pueda resolver ecuaciones complejas con gran precisión. Como señala un estudio reciente sobre su aplicación en ingeniería minera:
«Además, los nomogramas permiten que personas sin conocimientos previos resuelvan fórmulas complejas con una precisión adecuada».
Este enfoque es increíblemente poderoso. Elimina la barrera del conocimiento matemático avanzado y reduce drásticamente el riesgo de cometer errores al realizar cálculos manuales en tareas repetitivas. En la práctica, son más rápidos y fáciles de entender que los procedimientos analíticos tradicionales, ya que convierten un problema abstracto en una tarea visual sencilla.
3. A prueba de fallos: la robustez del papel frente a las pantallas.
En un mundo digital, la simplicidad del papel es una ventaja formidable. Los nomogramas destacan en entornos en los que los dispositivos electrónicos no son prácticos, como en operaciones de campo en minería, talleres mecánicos u obras. Sus ventajas son evidentes: son portátiles, resistentes y no necesitan electricidad ni conexión a internet.
Esta robustez los convierte en la herramienta ideal para realizar cálculos repetitivos sobre el terreno. Por ejemplo, un ingeniero de minas podría usar un nomograma impreso para determinar al instante el diseño correcto de una voladura, simplemente conectando líneas entre la densidad de la roca, la velocidad del explosivo y el diámetro de la perforación, y así reducir un cálculo complejo a una tarea visual simple y robusta sobre el papel.
4. El Renacimiento digital: cómo el código abierto revivió el nomograma.
Si los nomogramas son tan útiles, ¿por qué desaparecieron? Su principal inconveniente histórico no radicaba en su uso, sino en su creación. La parte más engorrosa era el dibujo matemático de las escalas graduadas, un proceso laborioso y especializado que probablemente fue una de las principales causas de su declive.
Aquí es donde entra en juego el software moderno. El resurgimiento de esta técnica se debe en gran parte a PyNomo y Nomogen, dos herramientas de código abierto basadas en Python. Fueron creadas por Leif Roschier y Trevor Blight, dos de los autores del estudio que ha inspirado este resurgimiento, que han unido así la experiencia académica con la programación moderna. Estas soluciones permiten a cualquier ingeniero o científico generar nomogramas complejos y precisos en cuestión de segundos, eliminando el obstáculo que los había hecho obsoletos.
5. Intuición visual: comprendiendo la relación entre las variables.
Además de su utilidad práctica, los nomogramas ofrecen una ventaja más sutil, pero profunda: fomentan la comprensión conceptual del problema. Mientras que una calculadora o un programa informático suelen funcionar como una «caja negra» que simplemente proporciona un resultado, un nomograma permite ver la relación entre las variables.
Esta visualización intrínseca de los datos permite una comprensión mucho más profunda. Al mover la isopleta (la regla) sobre el gráfico, un ingeniero puede desarrollar una intuición sobre cómo afecta un pequeño cambio en una variable a las demás, algo que se pierde al introducir simplemente números en un software. Por ello, se convierten en una poderosa herramienta didáctica.
Conclusión: lecciones de una sabiduría olvidada.
La historia del nomograma es un ejemplo fascinante de cómo las ideas del pasado pueden recuperar su relevancia gracias a la tecnología moderna. La combinación de una técnica de cálculo del siglo XVII con un software de código abierto del siglo XXI demuestra que no se trata solo de una reliquia, sino de una prueba de que las soluciones más simples y visuales pueden seguir siendo increíblemente valiosas.
Su regreso nos obliga a plantearnos una pregunta importante: en nuestra carrera constante hacia la digitalización, ¿qué otras herramientas analógicas e ingeniosas hemos olvidado que podrían ayudarnos a resolver los problemas del mañana?
Os dejo aquí una conversación en la que se tratan estos conceptos.
En este vídeo se resumen los conceptos más relevantes sobre los nomogramas.
Os dejo la comunicación que presentamos recientemente en el VII Congreso Nacional de Áridos. En ella se ilustran, proporcionan y explican detalladamente siete ejemplos originales de nomogramas que se utilizan para resolver ecuaciones comunes en la industria de la explotación de áridos, como el diseño de voladuras y la estimación de ratios de perforación.
Referencia:
MARTÍNEZ-PAGÁN, P.; YEPES, V.; ROSCHIER, L.; BLIGHT, T.; BOULET, D.; PERALES, A. (2025). Elaboración y uso de nomogramas para el ámbito de las explotaciones de áridos. Introducción de los códigos abiertos Pynomo y Nomogen. Actas del VII Congreso Nacional de Áridos, Córdoba, pp. 1085-1100. ISBN 978-84-125559-2-9.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.