Etiqueta: CRITIC

Comunicaciones presentadas al 29th International Congress on Project Management and Engineering AEIPRO 2025

Durante los días 16 y 17 de julio de 2025 tiene lugar en Ferrol (Spain) el 29th International Congress on Project Management and Engineering AEIPRO 2025. Es una buena oportunidad para debatir y conocer propuestas sobre dirección e ingeniería de proyectos. Nuestro grupo de investigación, dentro del proyecto de investigación RESILIFE, presenta varias comunicaciones. A continuación os paso los resúmenes.

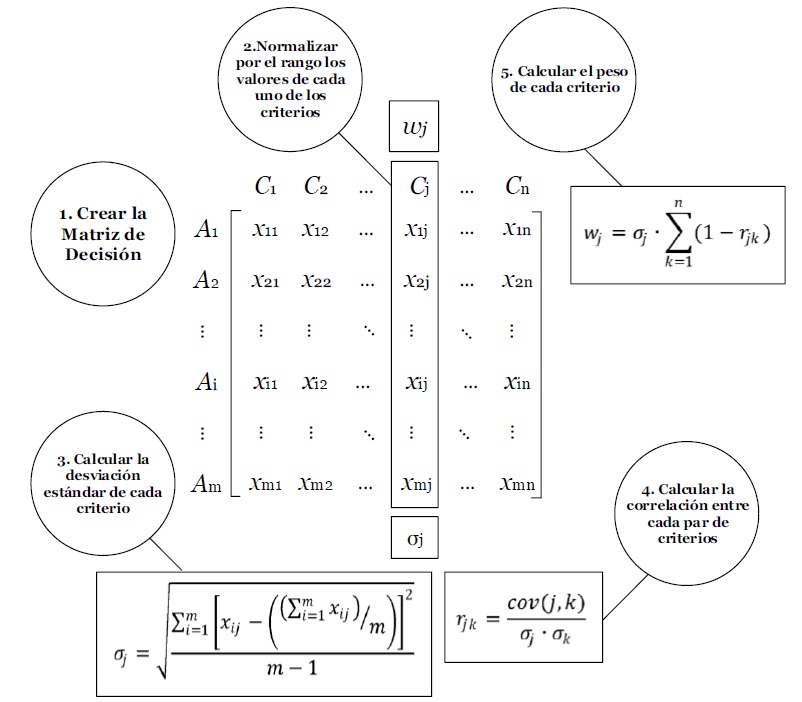
YEPES-BELLVER, L.; ALCALÁ, J.; YEPES, V. (2025). Optimización multiobjetivo de puentes de losa pretensada mediante el enfoque CRITIC-MCDM. 29th International Congress on Project Management and Engineering, AEIPRO, 16-17 de julio, Ferrol (Spain).

El trabajo establece una metodología para seleccionar el mejor diseño de un puente de losa pretensada, aplicando el método CRITIC de toma de decisiones multicriterio a un conjunto de soluciones establecidas mediante un muestreo por hipercubo latino que incluye los óptimos de cada función objetivo. Las funciones objetivo son el coste, las emisiones de CO₂ y la energía necesaria para construir una losa aligerada como paso superior. Esta metodología permite establecer una métrica sobre la que representar una superficie de respuesta que identifique las zonas donde las variables de diseño permiten reducir las tres funciones objetivo. Además, se analiza el método CRITIC aplicado a la frontera de Pareto de las soluciones y se estudia la robustez de la mejor opción en función de su distancia al punto ideal mediante tres métricas de Minkowski. Los resultados obtenidos indican la consistencia en la selección de la mejor solución.

YEPES-BELLVER, L.; MARTÍNEZ-PAGÁN, P.; YEPES, V. (2025). Nomogramas para el predimensionamiento económico de muros de retención de tierras. 29th International Congress on Project Management and Engineering, AEIPRO, 16-17 de julio, Ferrol (Spain).

Este trabajo presenta el desarrollo de una serie de nomogramas para el predimensionamiento económico de muros de retención de tierra con hormigón armado, empleados en la construcción de carreteras. Se propone un enfoque innovador para simplificar el proceso de diseño de estas estructuras, considerando una optimización económica que integra variables de geometría, materiales y refuerzo. Se incluyen alturas variables (de 4 a 10 m), teniendo en cuenta distintas condiciones de relleno y capacidad de soporte del terreno. Los resultados obtenidos proporcionan expresiones promedio que permiten calcular de manera práctica el coste total, el volumen de hormigón y acero, y las dimensiones geométricas de los muros. De este modo, se proporciona un marco de referencia útil para el diseño económico y eficiente de estos elementos estructurales en proyectos viales.

Os paso el vídeo promocional del Congreso.

Método CRITIC de toma de decisión multicriterio

Figura 1. Indecisión en la toma de decisiones

Dentro de los procedimientos de toma de decisiones multicriterio encontramos el método CRITIC (CRiteria Importance Through Intercriteria Correlation) propuesto por Diakoulaki, Mavrotas y Papayannakis en 1995. Se puede clasificar CRITIC dentro de los métodos comparativos. Con este método se obtienen pesos para cada uno de los criterios de forma que el peso es tanto mayor cuanta mayor sea su varianza (mayor desviación típica), y cuanta mayor información diferente a la de los otros criterios aporte (menor coeficiente de correlación entre criterios). Este método de ponderación de criterios se ha utilizado en diversos ámbitos como la valoración de empresas, inmuebles o jugadores de fútbol.

La metodología de CRITIC se puede resumir en los siguientes pasos:

  1. Crear la matriz de decisión
  2. Normalizar por el rango los valores de cada uno de los criterios
  3. Calcular la desviación típica de cada criterio
  4. Calcular la correlación entre cada par de criterios
  5. Calcular el peso de cada criterio

En la Figura 2 se puede ver un esquema de cálculo con este método (Bernal y Niño, 2018).

Figura 2. Método CRITIC (Bernal y Niño, 2018)

Para normalizar la valoración de cada alternativa respecto a cada criterio respecto al rango, hay que distinguir si se trata de un valor que quiere interesa ser incrementado (por ejemplo, un beneficio), o bien se trata de un valor que se desea que sea el más bajo posible (por ejemplo, un coste). En la Figura 3 se puede ver cómo se podría realizar dicha normalización.

Figura 3. Normalización por el rango (Bernal y Niño, 2018)

Supongamos que tenemos 5 alternativas para una estructura de hormigón que se va a evaluar respecto a 4 criterios: coste, beneficio, emisiones de CO2 y durabilidad. Si la matriz de decisión es la siguiente, invito al lector a calcular la mejor alternativa:

Coste Beneficio Emisiones Durabilidad
Alternativa 1 346 623 67 32
Alternativa 2 623 665 44 44
Alternativa 3 823 1000 98 26
Alternativa 4 556 344 33 33
Alternativa 5 234 666 23 53

Los pesos calculados con la metodología anterior serían los siguientes: Coste: 0,849; Beneficio: 1,565; Emisiones: 0,921 y Durabilidad: 0,710.

La valoración normalizada de cada alternativa sería la siguiente: Alternativa 1: 0,184; Alternativa 2: 0,213; Alternativa 3: 0,153; Alternativa 4: 0,133 y Alternativa 5: 0,316.

Por tanto, la Alternativa 5 sería la primera en ser seleccionada, mientras que la Alternativa 4 sería la última.

A continuación os dejo un vídeo explicativo del método realizado por el profesor Jerónimo Aznar Bellver, que espero que os sea de interés.

En este otro video se da un ejemplo de aplicación para valorar, en este caso, un apartamento.

Referencias:

AZNAR, J. (2020). Curso de valoración de activos por métodos multicriterio AHP, ANP y CRITIC. Editorial Universitat Politècnica de València. Ref. 264.

BERNAL, S.; NIÑO, D.A. (2018). Modelo multicriterio aplicado a la toma de decisiones representables en diagramas de Ishikawa. Universidad Distrital Francisco José de Caldas, Bogotá D.C., 137 pp.

DIAKOULAKI, D.; MAVROTAS, G.; PAPAYANNAKIS, L. (1995). Determining objective weights in multiple criteria problems – The CRITIC method. Computers & Operations Research, 22(7):763-770.