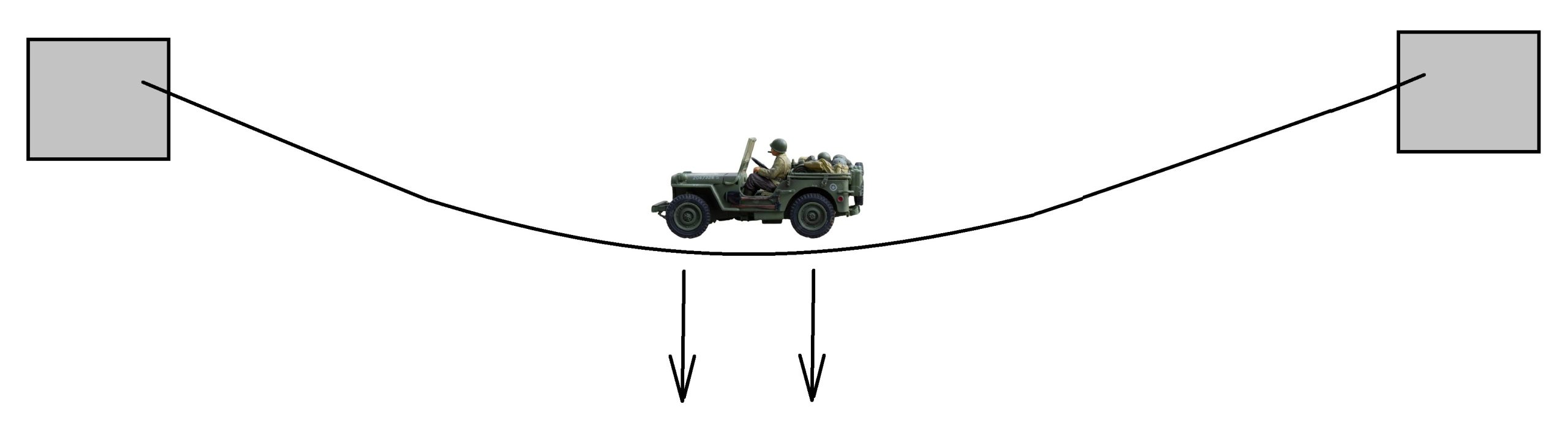
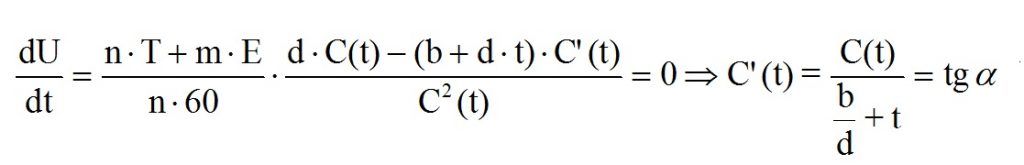Etiqueta: problema resuelto

El jeep que viaja por un cable, la rectificación del arco y la fórmula de Stevenin

Andaba estudiando 4º curso de la carrera de ingenieros de caminos, canales y puertos de Valencia, cuando en la asignatura de Procedimientos Generales de Construcción y Organización de Obras, el profesor Hermelando Corbí nos explicaba problemas de cables. Uno de dichos problemas lo he rescatado de mis viejos apuntes. Trata de un jeep que tiene que pasar por un puente militar formado por un cable. ¡Quién sabe cómo puede viajar un jeep por un solo cable! Pero bueno, el problema era el que era y había que resolverlo.

Con los planes de estudios actuales, los problemas de cables no se estudian en esta asignatura. Se reserva solo su estudio cualitativo, dejando a otras asignaturas de cálculo de estructuras este tema tan interesante.

El problema que os presento resuelto a continuación utiliza varias fórmulas dimensionales y aproximaciones que estudiábamos en aquel momento. Podéis ver cómo el problema sigue resuelto en unidades diferentes a las que empleamos ahora. Pero sirve para ver cómo ha cambiado la forma de plantear y resolver los problemas. Las expresiones usadas en el problema provienen del desarrollo teórico de las ecuaciones de equilibrio de un elemento de cable, de la ecuación fundamental de la estática de cables, de la rectificación del arco y de la fórmula de Stevenin.

Espero que este problema resuelto le traiga recuerdos a más de un compañero de promoción. Si encontráis alguna errata, por favor, me lo indicáis. Por cierto, si tenéis alguna fotografía de un jeep paseando por un puente militar formado por un solo cable, me lo mandáis.

Descargar (PDF, 277KB)

Referencias:

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

 

 

Funcionamiento de un cilindro neumático de simple efecto. Problema resuelto

A continuación te presentamos un problema resuelto de neumática, muy sencillo, que sirve de introducción a los conceptos básicos de los circuitos neumáticos aprovechando la capacidad de un pistón de simple efecto conectado a un motor con pérdidas mecánicas. Se trata de aprender cómo calcular la fuerza de avance y aplicar la Ley de Boyle al cálculo del volumen de aire en condiciones normales.

El enunciado del problema sería el siguiente: Un cilindro neumático de simple efecto, de 63 cm de diámetro y 10 cm de carrera, trabaja a una presión de 6 bares. Sabiendo que la fuerza neta ejercida en el vástago del cilindro es el 90% de la fuerza teórica, se pide:

  1. Fuerza neta ejercida por el cilindro en su carrera de avance.
  2. Consumo de aire medido en condiciones normales en una hora, si ese cilindro completa 6 ciclos de trabajo cada minuto.

Para ello os dejo el siguiente vídeo de Javier Luque que espero os sea útil.

Referencias:

YEPES, V.; MARTÍ, J.V. (2017). Máquinas, cables y grúas empleados en la construcción. Editorial de la Universitat Politècnica de València. Ref. 814. Valencia, 210 pp.

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Curva de llenado de una mototraílla empujada por buldócer

1ScraperDozer

Una mototraílla convencional, empujada por un buldócer, tiene una curva de llenado, función del tiempo de carga “t”: C=C(t). Sabiendo que el ciclo completo de las mototraíllas vale (a+t) y el de las empujadoras (b+d·t), siendo a, b y d constantes, calcular el tiempo de carga óptimo.

Resolución:

Como el material encuentra cada vez mayor resistencia a entrar en la caja de la traílla conforme esta se va llenando, la curva de carga es creciente, con un valor asintótico superior, que es la mayor capacidad de la traílla, a partir de la cual la misma cantidad de material que entra por abajo es derramado por su parte superior.

La curva C=C(t) tendría una forma como la que sigue:

Figura 1

El tiempo de carga óptimo es el que minimiza el coste unitario de producción U(t):

Figura 2

  • El coste horario del equipo, si este está formado por “n” traíllas, a un costo horario de “T” ptas/h, y “m” topadoras, a un coste horario de “E” euros/h, será:

Coste horario del equipo=n·T+m·E euros/h

 

  • La productividad horaria del equipo va a depender de si faltan o sobran traíllas.

* Si faltan traíllas, serán estas las que condicionen la producción total del equipo, que será:

Figura 8

En este caso

Figura 3

para encontrar el mínimo, derivamos e igualamos a cero:

Figura 10

Por consiguiente, para el cálculo del tiempo de carga óptimo basta con buscar la tangente de la curva de carga desde un punto situado a una distancia “a” del origen. “a” es el período del ciclo de la mototraílla que no se emplea en la carga.

Figura 5

* Si sobran traíllas, las topadoras condicionarán la producción total del equipo, que será:

Figura 9

En este caso

Figura 6

para encontrar el mínimo, derivamos e igualamos a cero:

Figura 7

Por tanto, de forma análoga al caso anterior, para el cálculo del tiempo de carga óptimo basta con buscar la tangente de la curva de carga desde un punto situado a una distancia “b/d” del origen.

Referencias:

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 253 pág.  ISBN: 84-7721-551-0.

YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Cursos:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Rendimiento de un motor térmico. Problema resuelto.

Seguimos en este artículo con problemas para nuestros alumnos que están de exámenes. Aprende a calcular el rendimiento de un motor térmico a partir de su velocidad de régimen y su par motor conociendo las características de su combustible. Evalúa cómo influye en el gasto que el motor sea de cuatro tiempos o de dos tiempos en idénticas condiciones de funcionamiento.

El enunciado del problema es el siguiente: Un motor de cuatro tiempos consume 8,47 litros a la hora de un combustible de 0,85 kg/dm³ de densidad y 41000 kJ/kg de poder calorífico. Entrega un par de 78,3 Nm a 3000 rpm. Se pide:

  1.  Calcular la masa de combustible consumida en cada ciclo
  2.  Calcular el rendimiento del motor
  3.  ¿Qué consecuencias tendría en el consumo/ciclo si el motor fuera de dos tiempos?

Para ello te dejo un vídeo de Javier Luque que espero te resulte de interés.

Referencias:

YEPES, V.; MARTÍ, J.V. (2017). Máquinas, cables y grúas empleados en la construcción. Editorial de la Universitat Politècnica de València. Ref. 814. Valencia, 210 pp.

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3