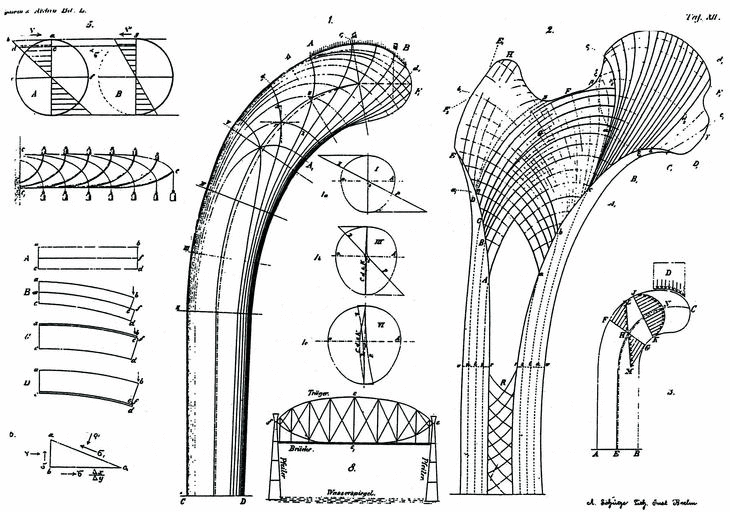
El desarrollo de la ingeniería de puentes ferroviarios se ha sustentado en el avance progresivo de disciplinas fundamentales como la resistencia de materiales y la mecánica estructural. A lo largo de los siglos XVII y XVIII, diversos científicos establecieron los fundamentos del análisis racional de estructuras. En 1678, Robert Hooke formuló la ley que relaciona la fuerza elástica con la deformación. En 1705, Jacob Bernoulli llevó a cabo un estudio exhaustivo sobre las curvas de deflexión. Leonhard Euler y Charles-Augustin de Coulomb fueron pioneros en la investigación de la estabilidad elástica de los elementos sujetos a compresión. Posteriormente, en 1826, Louis Navier sentó las bases de una teoría más exhaustiva de la elasticidad.
Francia ocupó una posición destacada en la promoción de estos avances durante el siglo XVIII, contribuyendo significativamente al desarrollo de ingenieros dotados de una sólida formación científica. Estos profesionales ejercieron una notable influencia en el campo de la ingeniería ferroviaria estadounidense. Dignos de mención son los ingenieros Charles Ellet (1830), Ralph Modjeski (1855), L. F. G. Bouscaren, ingeniero jefe del ferrocarril de Cincinnati Southern (1873) y H. E. Vautelet, ingeniero de puentes del Canadian Pacific Railway hacia 1876, quienes se formaron en las primeras escuelas de ingeniería francesas. Esta formación, fundamentada en un enfoque riguroso de las matemáticas, la mecánica y el análisis estructural, resultó determinante en el desarrollo de la ingeniería de puentes ferroviarios en América del Norte. En este contexto, los profesionales aplicaron los principios adquiridos en Francia, introduciendo un diseño más racional y científico en sus respectivos contextos ferroviarios. Entre 1885 y 1889, el ingeniero alemán F. Engesser, especializado en puentes ferroviarios, realizó importantes avances en el análisis de la estabilidad de los elementos comprimidos. Gracias a su trabajo, este tipo de estudios se pudieron generalizar para su aplicación práctica en ingeniería estructural, y los ingenieros disponían de herramientas más precisas para evaluar el riesgo de pandeo en columnas y otros elementos críticos de los puentes metálicos. Estos desarrollos fueron especialmente relevantes en un contexto de creciente demanda de estructuras más resistentes y fiables en la red ferroviaria europea.
Desde su nacimiento en la década de 1820, el ferrocarril se expandió rápidamente durante más de ochenta años. Este crecimiento constante, unido al aumento del peso de las locomotoras, provocó que muchos puentes tuvieran que ser reemplazados cada diez o quince años. La necesidad de estructuras más resistentes, con mayor luz y fiabilidad, unida a los fallos estructurales que se producían en servicio, impulsó a los ingenieros de mediados del siglo XIX a adoptar un enfoque más científico en el diseño de puentes de hierro y acero. A causa del elevado número de accidentes ferroviarios debidos a fallos estructurales en los puentes, la ingeniería de estos elementos experimentó una evolución significativa a lo largo del siglo XIX. Estos incidentes pusieron de manifiesto la necesidad urgente de adoptar un enfoque más riguroso y científico en el diseño y la evaluación de las estructuras, lo que impulsó una serie de investigaciones y avances técnicos fundamentales para garantizar la seguridad en el transporte ferroviario.
En Estados Unidos, esta práctica era principalmente empírica, basada en la experiencia y en la repetición de diseños de armaduras probadas, como las de tipo Town, Long, Howe y Pratt, en los que se mejoraban los materiales, pero sin un conocimiento profundo de las fuerzas internas. Este enfoque se reveló insuficiente entre 1850 y 1870, cuando se produjeron numerosos fallos estructurales. La necesidad de aumentar la seguridad y responder a cargas mayores llevó al desarrollo de métodos analíticos más rigurosos. En este contexto, Squire Whipple publicó en 1847 el primer análisis racional de celosías isostáticas mediante el método de los nudos, lo que supuso un hito en la historia de la ingeniería estructural.

Entretanto, en Europa, ingenieros franceses, alemanes y británicos también avanzaban en la teoría de la elasticidad y la mecánica estructural. En 1849, P. E. Clapeyron desarrolló la ecuación de los tres momentos, que aplicó en 1857 al análisis del puente Britannia. El diseño de este puente se basó en un análisis de tramos simples, a pesar de que Fairbairn y Stephenson eran conscientes de los efectos de la continuidad sobre la flexión. Los tramos se montaron inicialmente con apoyos simples y, posteriormente, se elevaron secuencialmente en los pilares correspondientes. Una vez en su posición, los tramos se conectaron mediante placas remachadas para lograr la continuidad del mismo, un enfoque innovador que permitió superar las limitaciones de los métodos tradicionales de construcción de puentes de la época. En el Reino Unido, los ingenieros ferroviarios realizaron ensayos con metales y modelos a escala para evaluar la resistencia y estabilidad de los puentes.
A partir de los trabajos de Whipple, dos ingenieros europeos destacaron especialmente: D. J. Jourawski y Karl Culmann. Jourawski criticó el uso de refuerzos verticales de placa empleados por Stephenson en el puente Britannia. Consideraba que esta solución no era la más adecuada para garantizar la resistencia y estabilidad del puente y destacaba la importancia de emplear métodos más eficientes en el diseño de elementos de compresión en estructuras de gran envergadura. Culmann, ingeniero del Ferrocarril Real Bávaro, fue un defensor temprano del análisis matemático de estructuras. En 1851, estudió en detalle las celosías como la Howe, ampliamente utilizadas en Estados Unidos. Karl Culmann no solo se centró en celosías isostáticas como las de tipo Howe, sino que también analizó estructuras hiperestáticas, como las celosías Long, Town y Burr. Estas configuraciones, más complejas desde el punto de vista estructural por ser estáticamente indeterminadas, fueron estudiadas por Culmann mediante métodos aproximados, lo que supuso un paso importante para comprender y evaluar este tipo de estructuras. Aunque no se disponía aún de herramientas matemáticas completamente desarrolladas para resolver estos sistemas con precisión, sus aproximaciones permitieron establecer criterios útiles para su diseño y validación en el contexto ferroviario de la época.
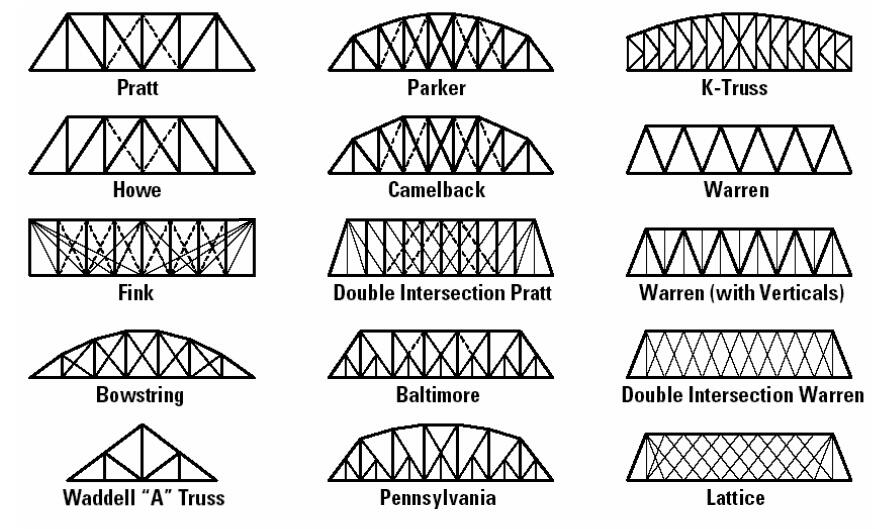
Durante esta misma época, se desarrollaron nuevas formas estructurales como la celosía Warren (1846) y W. B. Blood ideó en 1850 un método de análisis específico para armaduras trianguladas. La viga Warren, caracterizada por su estructura triangular regular y su eficiencia en la distribución de esfuerzos, se utilizó por primera vez en un puente ferroviario en 1853, en la línea del Great Northern Railway del Reino Unido. Este hecho marcó el inicio de su aplicación práctica en la infraestructura ferroviaria, consolidándose progresivamente como una de las tipologías estructurales más versátiles y extendidas en Europa y América del Norte.
En el Reino Unido, la investigación sobre los efectos de las cargas móviles y la velocidad también se inició en la década de 1850, precedida por los estudios teóricos de Stokes y Willis sobre vibraciones y resistencia. Fairbairn abordó en 1857 el impacto de estas cargas sobre estructuras isostáticas.
En 1862, el ingeniero alemán J. W. Schwedler presentó una teoría fundamental sobre momentos flectores y esfuerzos cortantes en vigas, y contribuyó al análisis de armaduras mediante el uso del método de secciones. Ese mismo año, A. Ritter perfeccionó dicho método al desarrollar un enfoque basado en el equilibrio en la intersección de dos barras de la armadura. Paralelamente, entre 1864 y 1874, James Clerk Maxwell y Otto Mohr desarrollaron y perfeccionaron los métodos gráficos para el análisis de celosías. Estas técnicas permitieron representar visualmente y con gran precisión los flujos de fuerza en las estructuras, lo que facilitó el diseño y la comprensión del comportamiento estructural.
Además, Maxwell y W. J. M. Rankine realizaron importantes aportaciones teóricas en ámbitos clave como los cables de suspensión en puentes metálicos, las vigas en celosía y los efectos de flexión, cortante, deformación y estabilidad en elementos comprimidos. Sus trabajos sentaron las bases de muchas de las prácticas modernas en ingeniería de estructuras metálicas y contribuyeron decisivamente al avance del diseño de puentes ferroviarios. Culmann también abordó el análisis de vigas continuas y largueros, y en 1866 publicó una descripción general del método para diseñar puentes en voladizo. En 1866, Karl Culmann publicó una descripción extensa y sistemática del análisis gráfico de celosías, consolidando así una metodología visual que permitió a los ingenieros calcular con mayor claridad y eficacia las fuerzas internas en estructuras complejas. Su obra no solo facilitó el diseño de puentes ferroviarios más seguros y eficientes, sino que también sirvió como referencia durante décadas en la enseñanza y práctica de la ingeniería estructural.
Posteriormente, Culmann desarrolló teorías sobre cargas móviles y flexión de vigas que fueron ampliamente aceptadas en Europa y Estados Unidos. En 1867, E. Winkler introdujo las líneas de influencia, una herramienta clave para el análisis de estructuras sometidas a cargas en movimiento.
El estudio de los efectos dinámicos del tráfico ferroviario, como los impactos derivados de las irregularidades de la vía, el «golpe de ariete» de las locomotoras, el cabeceo, el balanceo y la oscilación, continuó impulsando la investigación teórica y experimental. El aumento de la carga ferroviaria también generó preocupación por la fatiga del material, un campo en el que A. Wöhler destacó por sus estudios para los ferrocarriles alemanes.
A finales del siglo XIX, la ingeniería de puentes ferroviarios en Norteamérica dio un nuevo paso hacia la consolidación de una práctica plenamente científica. El ingeniero J. A. L. Waddell desempeñó un papel clave en este proceso, ya que en 1898 y 1916 publicó dos obras de referencia sobre el diseño de puentes de acero. Estos textos sentaron las bases de una metodología rigurosa y estandarizada para el diseño estructural en el ámbito ferroviario.
Hasta entonces, era habitual que las compañías ferroviarias adquiriesen puentes completos a fabricantes que ofrecían soluciones prefabricadas y de diseño propio. Waddell y otros ingenieros promovieron un cambio radical: que los diseños los realizaran de forma independiente, ingenieros cualificados basándose en principios científicos y que las empresas solo se encargaran de la fabricación. La Erie Railroad fue la primera en aplicar este nuevo modelo, y su ejemplo fue seguido rápidamente por el resto de compañías ferroviarias estadounidenses. Así, el diseño independiente y técnicamente fundamentado se convirtió en la norma.
Así, a comienzos del siglo XX, la ingeniería de puentes ferroviarios había alcanzado una madurez técnica plena en Estados Unidos y Europa, basada en fundamentos científicos sólidos, metodologías de cálculo avanzadas y una clara profesionalización del diseño estructural.
Os dejo un vídeo de un puente de ferrocarril en celosía tipo Warren.