El diseño estructural de infraestructuras, como edificios y puentes, se basa en códigos que establecen los criterios necesarios para garantizar su resistencia a diversas condiciones climáticas y ambientales. Estos códigos se actualizan periódicamente para reflejar los avances científicos y tecnológicos. Sin embargo, el cambio climático plantea un desafío disruptivo, ya que altera las condiciones climáticas de manera impredecible, lo que cuestiona la suposición de que las cargas climáticas son estacionarias.
El diseño estructural de infraestructuras, como edificios y puentes, se basa en códigos que establecen los criterios necesarios para garantizar su resistencia a diversas condiciones climáticas y ambientales. Estos códigos se actualizan periódicamente para reflejar los avances científicos y tecnológicos. Sin embargo, el cambio climático plantea un desafío disruptivo, ya que altera las condiciones climáticas de manera impredecible, lo que cuestiona la suposición de que las cargas climáticas son estacionarias.
En estas líneas se aborda cómo la transición del diseño estructural basado en estados límites ha influido en la forma en que se tienen en cuenta las variables climáticas. También aborda las dificultades que surgen al integrar el cambio climático en los modelos de riesgo estructural y analiza la necesidad de ajustar los métodos de estimación y diseño para tener en cuenta la creciente incertidumbre sobre el futuro climático.
Estas reflexiones se enmarcan dentro del proyecto RESILIFE, que actualmente desarrollo como investigador principal, y se han basado en algunas ideas desarrolladas en el trabajo reciente de Ellingwood et al. (2024).
Los códigos estructurales establecen los criterios necesarios para diseñar edificios, puentes y otras infraestructuras capaces de resistir las demandas de uso y los eventos ambientales o climáticos, como la nieve, el hielo, las lluvias, las tormentas de viento e inundaciones fluviales y costeras. Para garantizar que reflejen los últimos avances en ciencia e ingeniería, estos códigos se actualizan periódicamente, generalmente cada 5 o 10 años.
En las últimas cuatro décadas, los códigos estructurales de todo el mundo, como el «Minimum Design Loads and Associated Criteria for Buildings and Other Structures (ASCE 7-22)», las «LRFD Bridge Design Specifications (AASHTO)», el «International Building Code«, el «National Building Code of Canada» y los Eurocódigos, han adoptado los principios del diseño basado en estados límite. Durante este tiempo, los ingenieros estructurales y la normativa han reconocido la importancia de las herramientas de análisis de fiabilidad estructural y gestión del riesgo para modelar las incertidumbres asociadas a las cargas estructurales y la respuesta de las estructuras, y así garantizar un rendimiento adecuado en servicio (García-Segura et al., 2017). Con la transición del diseño basado en tensiones admisibles al diseño por estados límite, los criterios para las cargas climáticas han evolucionado gradualmente. Hasta ahora, estos criterios, basados en registros climáticos históricos y en evaluaciones de fiabilidad estructural, han tratado las cargas operativas y climáticas como estacionarias, asumiendo que el pasado es representativo del futuro.
El cambio climático plantea un desafío disruptivo y significativo para la evolución gradual de los códigos basados en el riesgo, así como para las prácticas de diseño estructural (ASCE, 2015a, 2018). La suposición de estacionariedad en el análisis de riesgos naturales deja de ser válida al tener en cuenta los efectos del cambio climático. Además, las incertidumbres asociadas a las proyecciones climáticas para el resto del siglo XXI son considerables, especialmente en lo que respecta a las cargas de viento, hielo y nieve (Tye et al., 2021). Las condiciones climáticas más agresivas podrían acelerar el deterioro estructural en ciertos casos, así como aumentar la intensidad y duración de los peligros. El cambio climático también ha suscitado controversia desde el punto de vista económico y político. Lograr consenso en los comités encargados de los códigos sobre el impacto del cambio climático en las infraestructuras requerirá una gestión técnica eficaz y una separación clara entre los aspectos políticos, como las causas del cambio climático, y los aspectos técnicos, como su impacto en las estructuras. Asimismo, podría haber oposición pública ante los costes adicionales que conlleven las modificaciones en los códigos climáticos. No obstante, ignorar los efectos del cambio climático en el comportamiento a largo plazo de las estructuras e infraestructuras podría incrementar el riesgo de daños y fallos, aumentar los costes de diseño, construcción y mantenimiento, agravar problemas de salud y seguridad públicas, interrumpir servicios esenciales y generar impactos socioeconómicos y ambientales negativos a nivel nacional.
Es fundamental abordar varias preguntas clave para considerar las exigencias del cambio climático en el desarrollo de los códigos estructurales. Entre ellas se encuentran (Ellingwood et al., 2024) :
- ¿Cómo se debe modelar la no estacionariedad en la ocurrencia e intensidad de los eventos climáticos extremos provocados por el cambio climático?
- ¿Cómo se deben integrar estas incertidumbres en un análisis de fiabilidad estructural dependiente del tiempo, con el fin de estimar el comportamiento futuro y demostrar el cumplimiento de los objetivos de rendimiento expresados en términos de fiabilidad?
- ¿Cómo se puede convencer a los ingenieros estructurales y al público en general de la necesidad de aceptar estos cambios en interés nacional (Cooke, 2015), incluso si en algunos casos los costes de los sistemas de infraestructura aumentan?
Problemas y desafíos en el análisis de datos climáticos para el diseño estructural
Las variables climáticas empleadas en los códigos estructurales se basan principalmente en datos históricos. Los vientos extratropicales, la nieve, la temperatura y las precipitaciones se analizan exclusivamente a partir de estos datos. En el caso de los huracanes, se integran datos históricos en un marco que modela su génesis en la cuenca del Atlántico Norte, su desarrollo hasta convertirse en huracanes plenamente formados que impactan en infraestructuras costeras y su disipación tras tocar tierra. Estos análisis suponen que las variables climáticas pueden evaluarse como si fueran estacionarias, es decir, que el pasado es representativo del futuro y que sus intensidades pueden determinarse en función de sus periodos de retorno. Los datos se han recopilado para fines distintos al diseño de edificaciones, como la aviación comercial, la hidrología local, la gestión de recursos hídricos y la agricultura, y generalmente abarcan menos de 100 años.
La mayoría de las variables climáticas incluidas en los códigos se suelen determinar ajustando el parámetro extremo anual a una distribución de probabilidad. Entre las distribuciones más comunes utilizadas para este propósito se encuentran la distribución Tipo I de valores máximos y la distribución generalizada de valores extremos. El periodo de retorno o intervalo medio de recurrencia de una carga se calcula como el recíproco de la probabilidad anual de que dicha carga se supere. El error de muestreo en la estimación de los eventos base de diseño en una secuencia estacionaria para periodos de retorno superiores a 100 años puede ser considerable. Sin embargo, las estimaciones de las medias de las muestras suelen ser razonablemente estables cuando se actualizan en intervalos típicos de 10 años con datos climáticos adicionales.
La suposición de estacionariedad en los datos no puede justificarse en un contexto de cambio climático (Pandey y Lounis, 2023), y el concepto de un evento asociado a un periodo de retorno específico no es aplicable en sentido estricto. El aumento (o disminución) de las variables climáticas, junto con la creciente incertidumbre en los modelos de predicción climática, especialmente a partir del año 2060, afectará a la forma de analizar y especificar los datos para fines de diseño estructural. Quizás lo más relevante sea el impacto que tendrá sobre la forma en que se comunicarán los peligros de diseño a la comunidad profesional de la ingeniería y a sus clientes (Cooke, 2015). Ellingwood et al. (2024) recuerdan claramente la confusión generada por el concepto de periodo de retorno cuando se introdujo a finales de la década de 1960. El periodo de retorno se concibió como una herramienta para reconocer que el parámetro de carga es aleatorio y para definir indirectamente la probabilidad anual de que se supere su intensidad de diseño, sin necesidad de recurrir a probabilidades pequeñas que no eran habituales entre los ingenieros estructurales de esa época. Esto podría explicar por qué algunos investigadores climáticos han intentado presentar sus estimaciones de parámetros utilizando el concepto de periodo de retorno (Ribereau et al., 2008; Salas y Obeysekera, 2014). Este problema requiere una reflexión cuidadosa al tratar con un clima cambiante, donde las probabilidades anuales no son constantes a lo largo de la vida útil de una estructura.
El crecimiento proyectado de las variables climáticas y sus incertidumbres más allá del año 2060 indica que será necesario desarrollar métodos para gestionar la incertidumbre epistémica -se refiere a la incertidumbre del modelo- en la estimación de parámetros, un aspecto que no se había tenido en cuenta previamente al estimar las variables climáticas para desarrollar códigos estructurales. Aunque la precisión de las técnicas generales de pronóstico climático ha mejorado gracias a la recopilación continua de datos, los modelos climáticos actuales son más capaces de predecir el impacto del cambio climático sobre la temperatura y las precipitaciones que sobre fenómenos como inundaciones, nevadas y vientos. Esto resulta problemático a la hora de considerar los niveles de probabilidad apropiados para el análisis de seguridad estructural.
Las futuras investigaciones podrían centrarse en el desarrollo de modelos más precisos para cargas climáticas específicas, como ciclones tropicales o sequías prolongadas, que aún presentan elevadas incertidumbres en sus proyecciones. Además, sería valioso explorar la aplicación de estos principios a sistemas de infraestructura emergentes, como redes de energía renovable o tecnologías de transporte resilientes. Por último, se sugiere investigar métodos para integrar datos climáticos en tiempo real en el diseño y seguimiento de infraestructuras, fomentando un enfoque dinámico y adaptable al cambio climático.
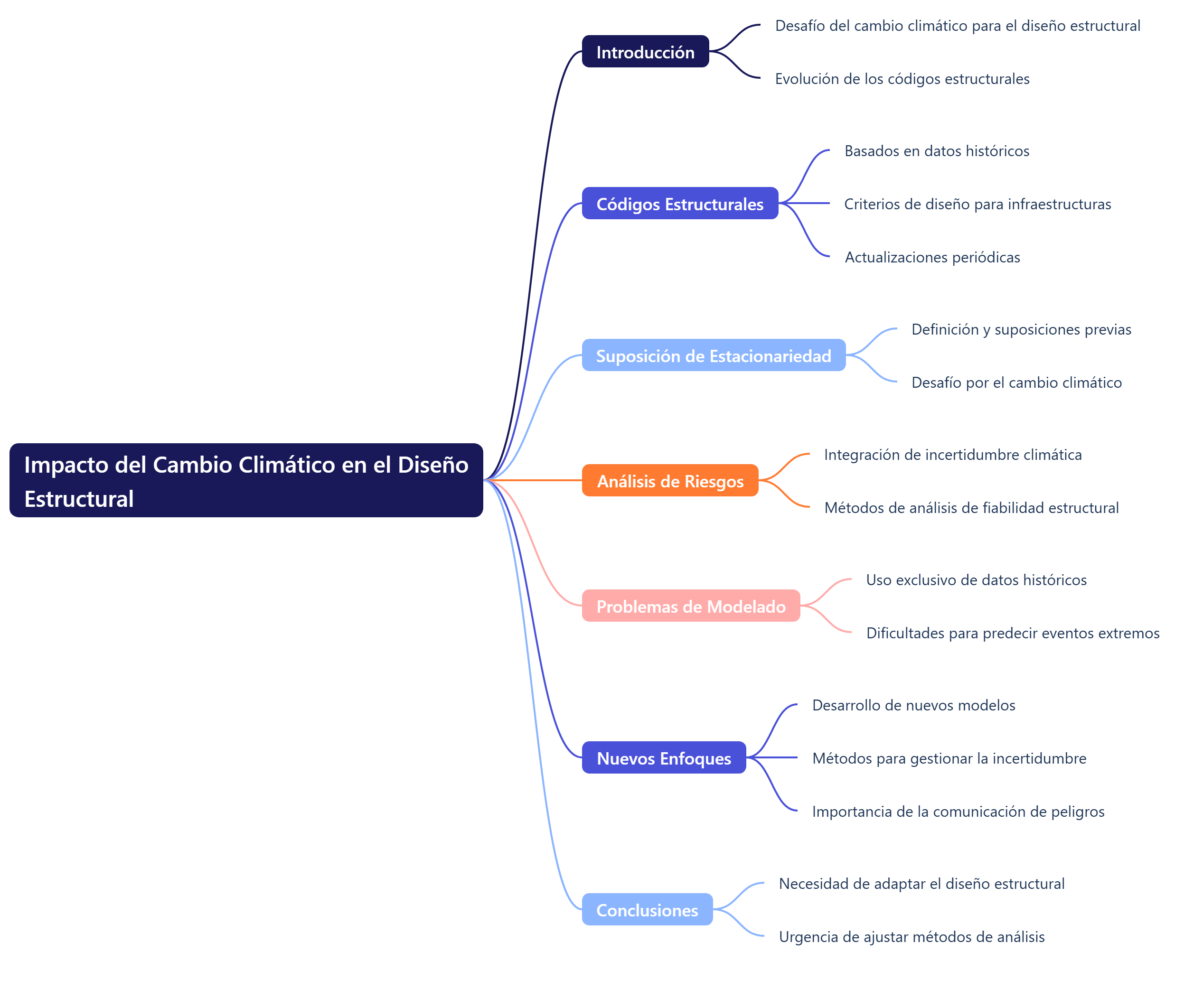
En resumen, los códigos estructurales establecen los criterios necesarios para diseñar infraestructuras capaces de resistir eventos climáticos como tormentas, nieve e inundaciones, y se actualizan periódicamente para reflejar los avances científicos y tecnológicos. Sin embargo, el cambio climático plantea un reto significativo, ya que altera las condiciones climáticas de manera impredecible, lo que hace que la suposición de estacionariedad que hasta ahora ha guiado el diseño estructural sea obsoleta. Este artículo explora cómo los códigos estructurales han evolucionado hacia un diseño basado en estados límite y la necesidad urgente de ajustar los métodos de análisis de riesgos ante la creciente incertidumbre climática. Además, se analizan los problemas derivados del uso exclusivo de datos históricos para modelar cargas climáticas y las dificultades que plantea el cambio climático a la hora de predecir eventos extremos. Finalmente, se destaca la necesidad de desarrollar nuevos modelos y enfoques analíticos que garanticen la seguridad de las infraestructuras en un entorno climático en constante cambio.
Os dejo un mapa conceptual sobre las reflexiones anteriores.
Referencias:
ASCE (2015). Adapting infrastructure and civil engineering practice to a changing climate. Committee on Adaptation to a Changing Climate. American Society of Civil Engineers.
ASCE (2018). Climate-resilient infrastructure: Adaptive design and risk management. Reston, VA: Committee on Adaptation to a Changing Climate. American Society of Civil Engineers.
Cooke, R. M. (2015). Messaging climate change uncertainty. Nature Climate Change, 5(1), 8-10.
Ellingwood, B. R., Bocchini, P., Lounis, Z., Ghosn, M., Liu, M., Yang, D., Capacci, L., Diniz, S., Lin, N., Tsiatas, G., Biondini, F., de Lindt, J., Frangopol, D.M., Akiyama, M., Li, Y., Barbato, M., Hong, H., McAllister, T., Tsampras, G. & Vahedifard, F. (2024). Impact of Climate Change on Infrastructure Performance. In Effects of Climate Change on Life-Cycle Performance of Structures and Infrastructure Systems: Safety, Reliability, and Risk (pp. 115-206). Reston, VA: American Society of Civil Engineers.
García-Segura, T., Yepes, V., Frangopol, D. M., & Yang, D. Y. (2017). Lifetime reliability-based optimization of post-tensioned box-girder bridges. Engineering Structures, 145, 381-391.
Pandey, M. D., & Lounis, Z. (2023). Stochastic modelling of non-stationary environmental loads for reliability analysis under the changing climate. Structural Safety, 103, 102348.
Ribereau, P., Guillou, A., & Naveau, P. (2008). Estimating return levels from maxima of non-stationary random sequences using the Generalized PWM method. Nonlinear Processes in Geophysics, 15(6), 1033-1039.
Salas, J. D., & Obeysekera, J. (2014). Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. Journal of hydrologic engineering, 19(3), 554-568.
Tye, M. R., & Giovannettone, J. P. (2021, October). Impacts of future weather and climate extremes on United States infrastructure: Assessing and prioritizing adaptation actions. Reston, VA: American Society of Civil Engineers.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.