Etiqueta: entropía

Desarrollo regional sostenible de la construcción basada en la teoría de la entropía

Acaban de publicarnos un artículo en Sustainability, revista indexada en el segundo cuartil del JCR. Se trata de aplicar la teoría de la entropía para evaluar el desarrollo sostenible de la construcción en una región determinada, en este caso, en China. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València.

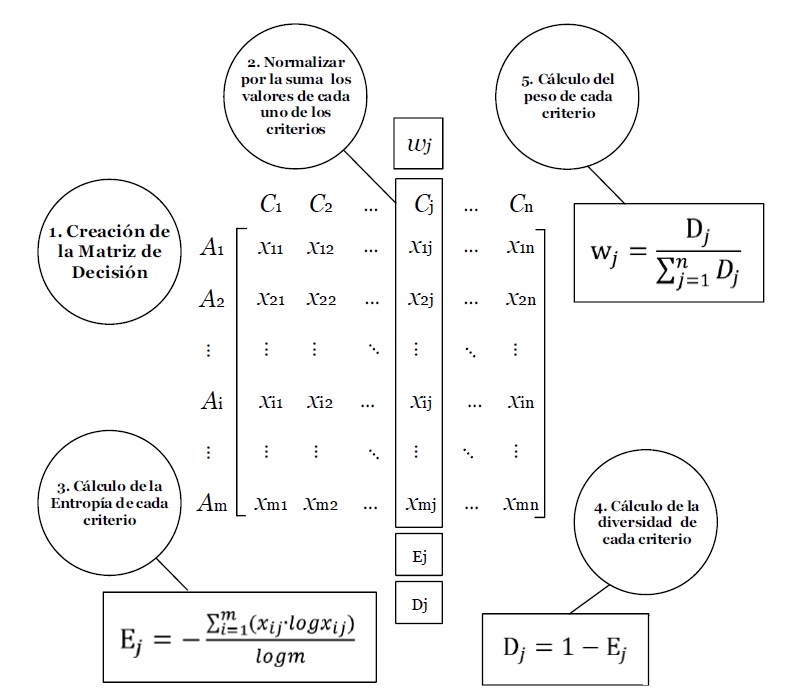
La humanidad se enfrenta actualmente al problema cada vez más urgente de la contaminación del medio ambiente. Para gestionar de forma rigurosa el medioambiente, los distintos gobiernos nacionales deberían basarse en bases científicas prácticas para ajustar y formular políticas y medidas legales basadas en el análisis de los datos existentes. En este trabajo se realiza un análisis basado en la teoría de la entropía de la innovación para evaluar el impacto de ocho provincias chinas, incluyendo los impactos ambientales, los económicos y los sociales. Los resultados muestran que los impactos en China deberían crecer desde 2021 hasta 2044 aproximadamente. Después de 2045, se estabilizarían, habiendo un crecimiento negativo en un corto período. La evaluación global del ciclo de vida (ECV) y la evaluación del impacto social (EIS) siguen siendo positivas. No habrá crecimiento negativo en los datos agregados y las emisiones serán nulas o negativas antes de 2108. Los datos finales de la investigación se presentan en forma de emisiones anuales, que proporcionan una base teórica para que el gobierno formule normativas y planes medioambientales a medio y largo plazo.

Abstract:

Human beings are now facing the increasingly urgent problem of global ecological environment pollution. To verify the scientific nature of environmental governance by governments of various countries, researchers need to provide a scientific basis and practical support for governments to adjust and formulate new policies and regulatory measures at any time through data analysis. This paper applies visual literature, aggregate analysis, engineering data programming, advanced mathematical science algorithms, and innovation entropy theory, and through this study, obtains sustainable impact data from eight Chinese provinces in the 21st century, including environmental, economic, and social impacts. The results show that China’s sustainable data should grow from 2021 to about 2044. After 2045, it will be stable, and there will be negative growth in a short period. The overall life cycle assessment (LCA) and social impact assessment (SIA) remain positive. There will be no negative growth in aggregate data and zero or negative emissions before 2108. The final research data are accurately presented in the form of annual emissions, which provide a scientific and theoretical basis for the government to formulate medium- and long-term ecological regulations and plans.

Keywords:

life cycle cost (LCC); life cycle assessment; social impact assessment; environment; bridge; carbon emissions

Reference:

ZHOU, Z.; ALCALÁ, J.; YEPES, V. (2022). Research on Sustainable Development of the Regional Construction Industry Based on Entropy Theory. Sustainability, 14(24): 16645. DOI:10.3390/su142416645

Como el artículo está publicado en abierto, os lo podéis descargar aquí mismo:

Descargar (PDF, 3.4MB)

Método de entropía para la toma de decisión multicriterio

Figura 1. Entropía. https://concepto.de/leyes-de-la-termodinamica/

Un procedimiento algo similar al método CRITIC que vimos en un artículo anterior, es el método de la entropía. Es un procedimiento propuesto por Zeleny en 1982 para calcular de forma objetiva el peso de cada uno de los criterios empleados en la toma de decisiones.

En este caso, la importancia de un criterio se supone que es proporcional a la cantidad de información intrísecamente aportada por el conjunto de alternativas respecto a dicho criterio. Se trata de dar mayor peso a aquel criterio que es capaz de discriminar mejor a las alternativas, es decir, aquel criterio que presente mayor diversidad en las valoraciones de las alternativas. La diversidad es menor cuanto mayor es la entropía, y por tanto, esta es la base del método.

El método de entropía se puede resumir en los siguientes pasos:

  1. Crear la matriz de decisión
  2. Normalizar por la suma los valores de cada uno de los criterios
  3. Calcular la entropía de cada criterio (se usan logaritmos en base 10)
  4. Calcular la diversidad de cada criterio
  5. Calcular el peso de cada criterio

En la Figura 2 se puede ver un esquema de cálculo con este método (Bernal y Niño, 2018).

Figura 2. Método de entropía (Bernal y Niño, 2018)

Para normalizar la valoración de cada alternativa respecto a cada criterio respecto a la suma, hay que distinguir si se trata de un valor que quiere interesa ser incrementado (por ejemplo, un beneficio), o bien se trata de un valor que se desea que sea el más bajo posible (por ejemplo, un coste). En la Figura 3 se puede ver cómo se podría realizar dicha normalización para el caso de valores que se incrementan. En caso de que disminuyan, se utiliza la inversa de dicho valor. Si hubieran valores negativos en los valores de las alternativas, antes de normalizar por suma, se añade una constante a cada una de las evaluaciones, de forma que sean mayores o iguales que cero.

Figura 3. Normalización por la suma (Bernal y Niño, 2018)

Supongamos que tenemos 5 alternativas para una estructura de hormigón que se va a evaluar respecto a 4 criterios: coste, beneficio, emisiones de CO2 y durabilidad. Si la matriz de decisión es la siguiente, invito al lector a calcular la mejor alternativa:

Coste Beneficio Emisiones Durabilidad
Alternativa 1 346 623 67 32
Alternativa 2 623 665 44 44
Alternativa 3 823 1000 98 26
Alternativa 4 556 344 33 33
Alternativa 5 234 666 23 53

Los pesos calculados con la metodología anterior serían los siguientes: Coste: 0,342; Beneficio: 0,168; Emisiones: 0,384 y Durabilidad: 0,106.

La valoración normalizada de cada alternativa sería la siguiente: Alternativa 1: 0,181; Alternativa 2: 0,177; Alternativa 3: 0,133; Alternativa 4: 0,184 y Alternativa 5: 0,325.

Por tanto, la Alternativa 5 sería la primera en ser seleccionada, mientras que la Alternativa 3 sería la última. Se invita al lector a comprobar los resultados respecto al método CRITIC, visto en un artículo anterior. La mejor alternativa se mantiene, pero la peor cambia.

A continuación os dejo un vídeo explicativo del método realizado por el profesor Jerónimo Aznar Bellver, que espero que os sea de interés.

https://media.upv.es/player/?id=a55342df-a14d-e547-875d-29329de4ba8d

En este otro vídeo, se da un ejemplo de valoración de una finca urbana.

https://media.upv.es/player/?id=83770294-668d-3b42-96f5-7438116b0faa

Referencias:

AZNAR, J.; GUIJARRO, F. (2012). Nuevos métodos de valoración: modelos multicriterio. Editorial Universitat Politècnica de València.

BERNAL, S.; NIÑO, D.A. (2018). Modelo multicriterio aplicado a la toma de decisiones representables en diagramas de Ishikawa. Universidad Distrital Francisco José de Caldas, Bogotá D.C., 137 pp.

ZELENY, M. (1982). Multiple Criteria Decision Making. Mc Graw Hill, New York, NY.