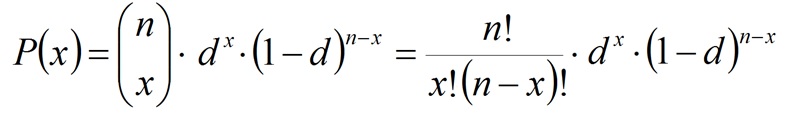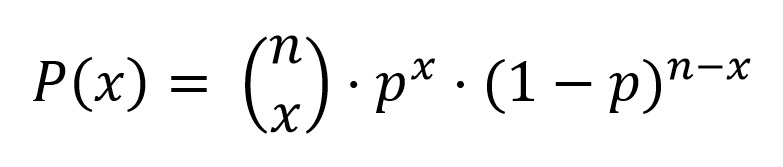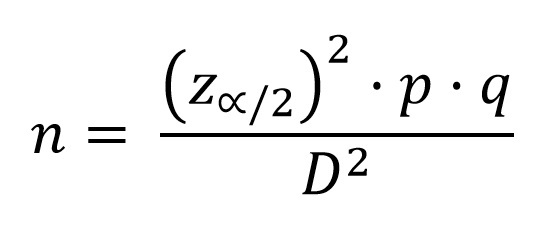Etiqueta: distribución binomial

Disponibilidad de un conjunto de máquinas iguales trabajando en paralelo

Figura 1. Retroexcavadora alimentando a un camión-dúmper. Imagen: V. Yepes

En obra es habitual que una máquina principal esté alimentando a un conjunto de máquinas auxiliares. Por ejemplo, en movimiento de tierras, una retroexcavadora puede estar cargando a un conjunto de camiones-dúmper (Figura 1). Otro ejemplo es un buldócer que está empujando a un equipo de mototraíllas convencionales. En estos casos, si se avería una máquina auxiliar, el resto de unidades puede seguir trabajando, aunque con una menor producción. Pues bien, se dice que un equipo de máquinas auxiliares está trabajando en paralelo entre ellas. Sin embargo, el conjunto de máquinas auxiliares trabaja en serie o en cadena respecto a la principal, pues el fallo de la máquina principal, o del total de las auxiliares, paraliza al conjunto. Veamos cómo podemos calcular la disponibilidad intrínseca de un conjunto de máquinas iguales que trabaje en paralelo sabiendo que la disponibilidad intrínseca de cada una de ellas es d.

Sean n máquinas iguales trabajando en paralelo, con una disponibilidad intrínseca d. Si se dispone de un conjunto suficientemente grande de unidades, una fracción d de ellas se encontrarán en disposición, y otra fracción (1-d) no operativas. Si se extrae una muestra n de ellas -las que forma nuestro equipo-, la probabilidad de que se encuentren x máquinas en disposición sigue una distribución binomial:

La probabilidad que el equipo esté parado, es decir, que ninguna de las máquinas se encuentre activa será:

y la probabilidad de que el equipo se encuentre en disposición, aunque sea solo una de las máquinas será:

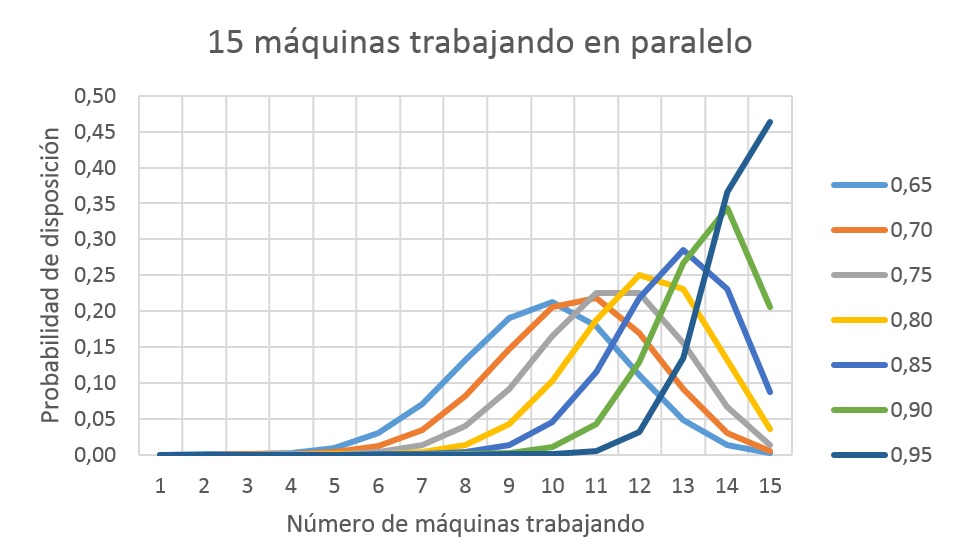
En la Figura 2 se muestra la probabilidad de que se encuentren x máquinas trabajando en paralelo operativas en un equipo de 15 en función de la disponibilidad intrínseca. Por ejemplo, para d = 0,80 lo más probable es que se encuentren 12 máquinas trabajando, siendo casi despreciable la probabilidad que trabajen menos de 6 unidades. Se observa que la probabilidad máxima aumenta con la disponibilidad intrínseca.

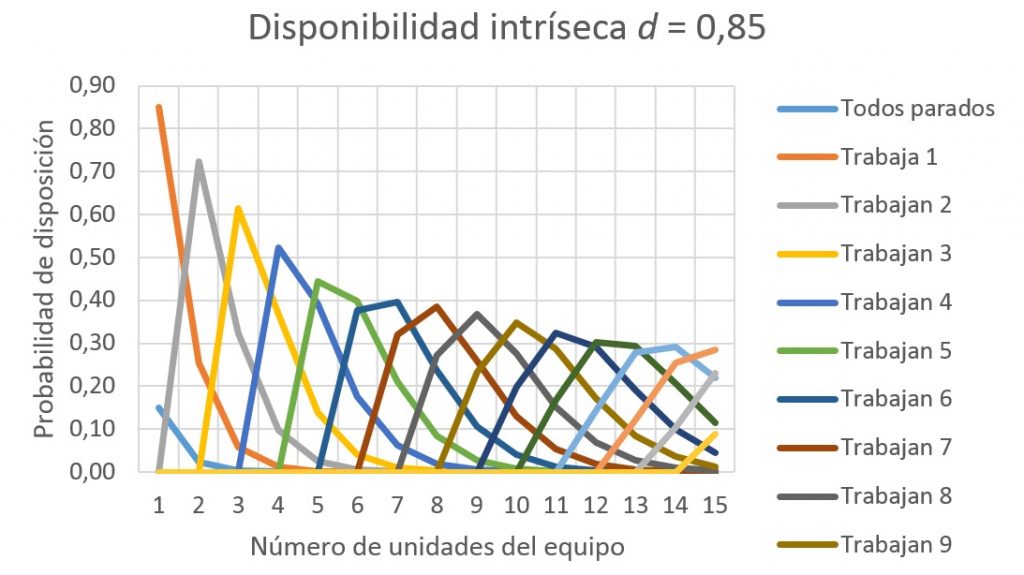
Figura 2. Probabilidad de que se encuentren trabajando x máquinas en paralelo en función de la disponibilidad intrínseca para un equipo de 15 máquinas. Elaboración propia.

En la Figura 3 se muestra la probabilidad de disposición de un conjunto de máquinas trabajando en paralelo en función del número de unidades del equipo y la cantidad de ellas que se encuentran trabajando, para una disponibilidad intrínseca d = 0,85. Por ejemplo, para un conjunto de 10 unidades, la probabilidad de que se encuentren trabajando 9 de ellas, es del 34,7%. Como resulta evidente, si hay solo un equipo, la probabilidad de que trabaje es del 85%, que coincide con su disponibilidad intrínseca. Se observa que las probabilidades máximas de disposición disminuyen conforme aumenta el número de unidades del equipo y la exigencia de que esté un número mayor de ellas trabajando.

Figura 3. Probabilidad de que se encuentren trabajando x máquinas en paralelo en función del número de unidades del equipo y del número de ellas que se encuentren activas, para una disponibilidad intrínseca d = 0,85. Elaboración propia.

 

Referencias:

PELLICER, E.; YEPES, V.; TEIXEIRA, J.C.; MOURA, H.P.; CATALÁ, J. (2014). Construction Management. Wiley Blackwell, 316 pp. ISBN: 978-1-118-53957-6.

ROJO, J. (2010). Manual de movimiento de tierras a cielo abierto. Fueyo Editores, S.L., Madrid, 926 pp.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente nº 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.

YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

 

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Medición del trabajo a través del procedimiento de observaciones instantáneas

Las observaciones instantáneas constituye un procedimiento de medición del trabajo que, junto con el cronometraje, permite determinar los tiempos improductivos y sus causas, eliminándolas mediante su análisis. Se emplea como auxiliar del estudio de métodos para eliminar o disminuir el tiempo de trabajo. El cronometraje es más apropiado para trabajos muy sistematizados y repetitivos, efectuados por una o pocas unidades de recurso. En cambio, las observaciones instantáneas cubre el resto de los escenarios posibles, como trabajos poco sistematizados, con ciclos largos o realizados por numerosos recursos.

Las observaciones instantáneas se basan en comprobar si, en un momento dado, un recurso se encuentra trabajando o parado. Se puede estimar el tiempo de trabajo y el de parada, así como su error estadístico basándose en la distribución binomial de probabilidad. Se puede ejecutar una pasada si observamos a un conjunto de recursos y anotamos para cada uno de ellos su situación de trabajo o parada. Para planificar correctamente las observaciones, se debería garantizar que todas las actividades sean observadas un número de veces proporcional a su duración.

Detengámonos un momento en el fundamento estadístico del método. Supongamos que p es la fracción del tiempo en el que un recurso presenta una característica. Por ejemplo, si p=15% puede significar que, del tiempo total de permanencia de una máquina en una obra, el 15% del tiempo se encuentra parada. Si extraemos n elementos de la población infinita de posibilidades en las que una máquina puede estar parada en una proporción p en una obra, la probabilidad de que x máquinas se encuentren paradas sería la siguiente:

Si en la distribución binomial se cumple que n·p>15, entonces la distribución binomial —que es discontinua— se puede aproximar a la distribución normal —que es continua—.

Ahora lo que nos interesa es conocer el tamaño de la muestra n para proporciones en una población infinita. Para calcular este tamaño de muestra, antes debemos especificar el nivel de confianza con el que se desea realizar la estimación y el margen de error máximo tolerable D. De esta forma, se espera trabajar con una muestra que sea representativa y que las estimaciones sean consistentes. La expresión que utilizaremos será la siguiente:

Aquí os dejo una tabla que relaciona el nivel de confianza con los las variables utilizada en la fórmula anterior:

Nivel de confianza α Z α/2 (Z α/2)2
99% 0,01 2,576 6,636
95% 0,05 1,960 3,842
90% 0,10 1,645 2,706
80% 0,20 1,280 1,638
50% 0,50 0,674 0,454

 

También os dejo un vídeo explicativo y un problema resuelto.

Descargar (PDF, 100KB)

Referencia:

YEPES, V. (2015). Coste, producción y mantenimiento de maquinaria para construcción. Editorial Universitat Politècnica de València, 155 pp. ISBN: 978-84-9048-301-5.

Licencia de Creative Commons
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.