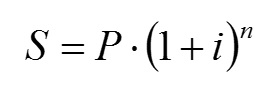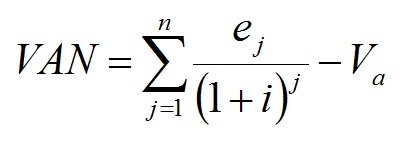Uno de los problemas que tiene una empresa constructora es elegir adecuadamente la maquinaria habida cuenta de la elevada inversión que debe realizar. En un artículo anterior ya se indicaron los condicionantes a tener en cuenta en su selección.
Cuando se trata de elegir una máquina por su rentabilidad económica, hay que tener presente que se generan unos flujos de costes y de beneficios a lo largo del periodo utilización. Por tanto, ante la presencia de varias alternativas, os podemos hacer dos preguntas: ¿Qué criterio se puede utilizar para elegir la más ventajosa? ¿Está justificada la inversión de esta alternativa?
Para elegir la mejor opción de compra posible, se puede realizar un estudio que maximice la rentabilidad económica considerando o no la actualización monetaria de la inversión. Entre los métodos sin actualización económica destacamos los siguientes:
- Rentabilidad media de la inversión: Se opta por aquella máquina que produce la tasa de rendimiento medio más alta, es decir, el mayor cociente entre la suma de los beneficios netos generados durante la vida de la inversión y el coste de adquisición. Los beneficios netos son la diferencia entre los ingresos brutos y los gastos, considerando la amortización de la inversión. Una variante a este método sería calcular la rentabilidad teniendo en cuenta la inversión media del equipo y no el valor de compra.
- Recuperación de la inversión o periodo de retorno: Se elige aquella máquina que minimiza el tiempo necesario para que los beneficios netos generados igualen al precio de adquisición de la inversión. En este método no importa la rentabilidad de la inversión. Puede ser útil cuando los inversores estén interesados en recuperar lo antes posible los fondos aportados.
Por otra parte, el valor del dinero depende del tiempo, puesto que los intereses gravan la disponibilidad del dinero prestado. Así, dada una tasa de actualización i en tanto por uno, y n periodos de tiempo, una cantidad actual P y una futura S están relacionadas entre según la siguiente expresión:
De esta forma, las comparaciones intertemporales de las unidades monetarias deben realizarse con los ingresos o gastos actualizados. En estos cálculos, además, debería considerarse las expectativas de inflación. Sin embargo, normalmente la inflación futura conlleva una elevación de los valores monetarios, con lo que los rendimientos y costes serían los mismos. No obstante, no siempre ocurre este supuesto, por lo que se puede complicar el cálculo. Se pueden considerar los siguientes métodos con actualización monetaria:
- Valor actual neto: Se elige aquella máquina que maximiza la diferencia entre el valor actual de los ingresos netos y el coste de la inversión (VAN). Siendo ej los ingresos netos en el año j, n el número de periodos e i la tasa de interés, el valor actual de los ingresos se calcula como:
Al calcular el VAN debería incluirse el valor residual actualizado, es decir, son los beneficios de liquidación al final del periodo de inversión. Pero también podríamos hablar de una plusvalía de liquidación negativa si durante el transcurso del plazo de inversión se producen costes, como, por ejemplo, de eliminación o retirada.
Una adquisición será rentable si el VAN es positivo. Ello significa que la inversión genera más beneficios que un depósito bancario con la tasa de actualización seleccionada. Si el VAN es cero, la inversión no ofrece ninguna ventaja sobre un depósito bancario, generando únicamente como beneficio el tipo de descuento.
- Tasa interna de rentabilidad: Se elige la máquina con mayor tasa interna de rentabilidad (TIR), definida como el valor de i que anula el VAN. Una de las ventajas es que no se necesita conocer i para su cálculo. La inversión será interesante si el TIR supera la tasa de interés del mercado. Se puede decir que el TIR es el porcentaje de beneficio o pérdida que se puede obtener de una inversión.
Algunos autores recomiendan recurrir al valor más alto del TIR como criterio de selección de equipos. La pregunta es si coincidiría entonces esta selección para una tasa dada de actualización, con la que se obtendría con el criterio del VAN. Para responder a esta pregunta, supondremos la situación de dos equipos A y B, cuyos valores actualizados netos son VANA (i) y VANB (i), como se muestra en la Figura 2.
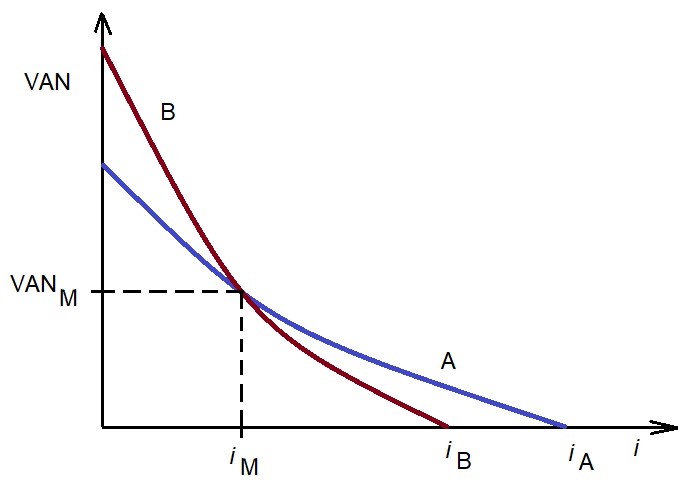
Si el criterio de elección es el del TIR, el equipo A será seleccionado, pues iA > iB. Al seleccionar en función del VAN, se adoptaría el equipo B para tasas de actualización comprendidas entre 0 e iM, y para mayores valores, el equipo A. Este valor de iM se denomina tasa de comparación de los equipos A y B, y en ella coinciden sus VAN.
Por tanto, se puede concluir que el criterio de la TIR es útil para comparar el valor correspondiente con la tasa de actualización, ya que, si es inferior a este valor, se debe rechazar la alternativa. Cuando se trata de elegir el equipo óptimo entre otros incompatibles con él, se debe utilizar el criterio del VAN, que nos permite determinar la mejor inversión. Mientras el VAN calcula la rentabilidad de la inversión en términos monetarios actualizados, el TIR realiza el análisis de esa rentabilidad en forma de porcentaje.
Os dejo algunos vídeos donde se explica cómo calcular el VAN y el TIR.
Referencias:
LIDÓN, J. (1998). Economía en la construcción I. Editoral de la Universidad Politécnica de Valencia, 366 pp.
PELLICER, E.; YEPES, V.; TEIXEIRA, J.C.; MOURA, H.P.; CATALÁ, J. (2014). Construction Management. Wiley Blackwell, 316 pp. ISBN: 978-1-118-53957-6.
PÉREZ GOROSTEGUI, E. (2021). Dirección de empresas. Editorial Universitaria Ramón Areces, 784 pp.
YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente nº 97.439. Ed. Universitat Politècnica de València. 253 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.
YEPES, V. (2015). Coste, producción y mantenimiento de maquinaria para construcción. Editorial Universitat Politècnica de València, 166 pp. Ref. 402. ISBN: 978-84-9048-301-5.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.