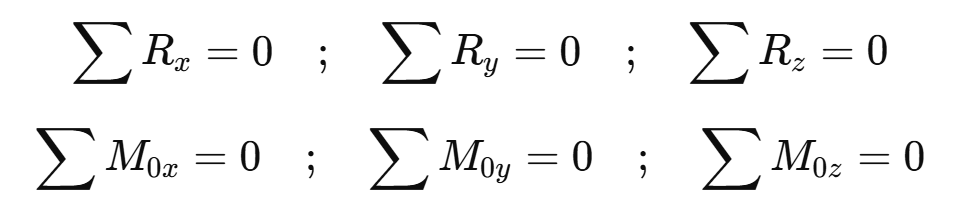Este artículo explora la evolución del concepto de material en mecánica aplicada, comenzando por el modelo idealizado de sólido rígido, que simplifica los cuerpos indeformables para análisis iniciales. Sin embargo, al abordar la mecánica aplicada, esta abstracción se rompe y es necesario introducir el sólido elástico, que permite la deformación reversible y el análisis de tensiones internas. Aunque este modelo asume isotropía, homogeneidad y continuidad, se reconoce que ningún material real cumple estas condiciones. Finalmente, se introduce el concepto de sólido verdadero, que reconoce la complejidad de los materiales reales y sus propiedades variables, aunque se puede simplificar para su estudio mediante la división en zonas homogéneas, cada una de las cuales se modela como un sólido elástico. Este tránsito conceptual es crucial para la ingeniería y la resistencia de materiales, ya que permite el diseño de estructuras seguras y funcionales que consideran la deformación y los límites de carga de los materiales reales.
En los primeros planteamientos de la mecánica teórica, los cuerpos materiales se consideran como sólidos indeformables, con independencia de si se encuentran en reposo o en movimiento. Esta hipótesis, evidentemente ideal, no se corresponde con ningún material real, pero resulta extraordinariamente útil por la simplificación conceptual y matemática que introduce en el análisis.
Pese a tratarse de una abstracción, sus resultados son, en muchos casos, aproximaciones aceptables del comportamiento físico real, especialmente cuando las cargas implicadas son pequeñas y las deformaciones son pequeñas. No obstante, cuando el estudio se adentra en el terreno de la mecánica aplicada, esta simplificación empieza a mostrar sus límites.
La ruptura del modelo ideal: la necesidad de una nueva definición de sólido
La observación experimental revela que no se pueden aplicar fuerzas indefinidamente a un cuerpo sin que se deforme o incluso se rompa. Esta evidencia obliga a revisar el concepto de sólido aceptado en la teoría mecánica.
Este proceso de revisión y refinamiento lleva a una evolución del modelo de sólido, especialmente a partir del estudio más profundo de los problemas de estática aplicada. En este contexto, es necesario distinguir entre tres concepciones del sólido:
- Sólido rígido
- Sólido elástico
- Sólido verdadero
1. Sólido rígido: el modelo idealizado
Se denomina sólido rígido al que no altera su estructura interna por acción exterior, manteniendo constantes las distancias entre sus moléculas, independientemente de la magnitud o naturaleza del esfuerzo aplicado. Esta suposición permite abordar problemas mecánicos aplicando exclusivamente las condiciones de equilibrio:
donde las Ri son las componentes de la resultante de las fuerzas, y los M0i los momentos respecto de un punto cualquiera O, en un sistema cartesiano trirrectangular.
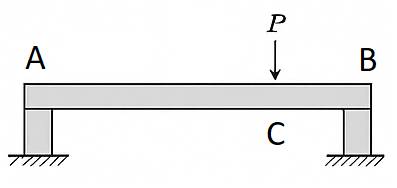
Sin embargo, este modelo resulta incompatible con la realidad física. Supongamos una viga AB, apoyada sobre dos pilares, que recibe una carga vertical P en un punto intermedio C. Si se asume que la viga es un sólido rígido, el problema se resuelve calculando las reacciones de los apoyos, sin que exista posibilidad de rotura, con independencia del valor de P. No obstante, la experiencia demuestra que, a partir de un cierto valor de P, la viga se rompe, incluso si las reacciones están equilibradas.
Esto pone de manifiesto una limitación estructural del modelo de sólido rígido, y evidencia la necesidad de estudiar no solo el equilibrio exterior, sino también la resistencia interna del material frente a esfuerzos aplicados.
2. Sólido elástico: deformabilidad reversible
La respuesta a esta necesidad se encuentra en el concepto de sólido elástico, entendido como aquel cuerpo que, al ser sometido a una fuerza exterior, se deforma, pero recupera su forma original cuando dicha acción cesa. Este modelo admite una deformación interna y, por tanto, un reparto espacial de los esfuerzos, lo que permite analizar no solo si el sistema está en equilibrio, sino también cómo se manifiestan las tensiones en su interior.
Para que el modelo elástico sea tratable matemáticamente, se hacen ciertas hipótesis simplificadoras que, si bien no se cumplen con exactitud en la práctica, ofrecen una base coherente para el cálculo:
- Isotropía: el material presenta las mismas propiedades mecánicas en todas las direcciones.
- Homogeneidad: cualquier porción del sólido tiene idéntica composición y comportamiento que otra cualquiera.
- Continuidad: no existen huecos ni discontinuidades internas; la materia se distribuye de forma continua en el espacio.
Estas hipótesis están estrechamente relacionadas. Si se admite que un material es elástico en todas las direcciones, parece lógico suponer que su estructura es homogénea, y viceversa.
3. La realidad material: límites del modelo elástico
Ningún material real satisface de forma rigurosa estas condiciones.
- La isotropía perfecta no existe, debido a que la estructura atómica o molecular del material presenta orientaciones privilegiadas.
- La homogeneidad absoluta tampoco se cumple, pues siempre existen variaciones locales en la composición.
- Finalmente, la materia no es continua: existen espacios vacíos entre moléculas, e incluso en el interior de los átomos, como muestran las teorías físicas actuales.
A pesar de ello, el hecho de considerar el sólido como continuo y elástico sigue siendo útil y válido a efectos prácticos. Permite suponer que las fuerzas aplicadas a una porción del material se transmiten de forma progresiva a sus regiones vecinas, generando un campo de tensiones continuo y calculable. Aunque la elasticidad no sea exacta a escala microscópica, funciona a escala macroscópica, como demuestra la experiencia acumulada en el diseño y comprobación de estructuras.
4. Sólido verdadero: el material tal como es
El último nivel de descripción lo proporciona el concepto de sólido verdadero, que reconoce explícitamente que los materiales reales no son ni rígidos ni elásticos ideales. Carecen de isotropía, homogeneidad y continuidad, por lo que requieren un tratamiento más refinado. En este caso, el material se considera un sólido deformable, con una estructura interna compleja y propiedades variables.
Aunque este enfoque representa la forma más fiel de representar un material real, su complejidad puede superarse dividiendo el material en zonas homogéneas. Entonces, cada una de estas zonas puede modelarse como un sólido elástico, lo que permite aplicar la teoría correspondiente de forma localizada.
Consideración final
En el estudio de la resistencia de materiales, nos ocupamos precisamente de determinar los límites de carga admisibles o las dimensiones necesarias de un elemento estructural para garantizar que, bajo los esfuerzos previsibles, no se produzca la rotura. Si existieran verdaderos sólidos rígidos, tales cálculos serían innecesarios, ya que bastaría con verificar el equilibrio de fuerzas y momentos. Sin embargo, dado que todos los materiales reales se deforman incluso antes del fallo, la teoría de la elasticidad y la resistencia de materiales resultan indispensables para la ingeniería civil.
Así, el tránsito desde el modelo de sólido rígido hasta el de sólido verdadero no solo es un refinamiento teórico, sino una adaptación necesaria a la realidad física de los materiales que permite a los ingenieros diseñar estructuras seguras, funcionales y duraderas.
Glosario de términos clave
- Sólido rígido: Modelo idealizado de cuerpo material que se considera indeformable; mantiene constantes las distancias entre sus moléculas independientemente de las fuerzas aplicadas. Útil para análisis de equilibrio, pero no para predicción de resistencia o rotura.
- Sólido elástico: Modelo de cuerpo que se deforma bajo la acción de una fuerza exterior, pero recupera su forma original cuando dicha acción cesa. Admite deformación interna y reparto de esfuerzos, permitiendo el análisis de tensiones.
- Sólido verdadero: Concepto que reconoce la realidad física de los materiales, que no son ni rígidos ni elásticos ideales. Carecen de isotropía, homogeneidad y continuidad perfectas, y poseen una estructura interna compleja y propiedades variables.
- Mecánica teórica: Campo de la mecánica que en sus primeros planteamientos consideraba los cuerpos materiales como sólidos indeformables, buscando simplificación conceptual y matemática.
- Mecánica aplicada: Campo de la mecánica que se adentra en el estudio de problemas reales donde la simplificación del sólido rígido es insuficiente, requiriendo considerar la deformación y resistencia de los materiales.
- Equilibrio (condiciones de): Principios que rigen la estática y dinámica de cuerpos, asegurando que la resultante de fuerzas y momentos sea cero. En el sólido rígido, son suficientes para la resolución de problemas.
- Resistencia interna del material: Capacidad de un material para soportar esfuerzos aplicados sin romperse o deformarse permanentemente. Es un concepto clave en la mecánica aplicada y la teoría de la elasticidad.
- Deformación: Cambio en la forma o dimensiones de un cuerpo bajo la acción de fuerzas externas.
- Tensiones (campo de): Distribución interna de fuerzas por unidad de área dentro de un material deformado. El modelo elástico permite su cálculo.
- Isotropía: Propiedad de un material que presenta las mismas propiedades mecánicas en todas las direcciones. Es una hipótesis simplificadora del modelo elástico.
- Homogeneidad: Propiedad de un material que tiene idéntica composición y comportamiento en cualquier porción de su volumen. Es una hipótesis simplificadora del modelo elástico.
- Continuidad: Hipótesis que asume que la materia se distribuye de forma continua en el espacio, sin huecos ni discontinuidades internas. Es una idealización del modelo elástico.
- Resistencia de materiales: Rama de la ingeniería y la mecánica aplicada que estudia el comportamiento de los cuerpos sólidos deformables bajo diferentes tipos de carga, con el objetivo de determinar sus límites de carga admisibles y dimensiones necesarias para evitar la rotura.