algoritmos archivos - El blog de Víctor Yepes

Docencia e inteligencia artificial: nuevas estrategias para educadores

La educación está experimentando una transformación sin precedentes gracias a los avances en inteligencia artificial (IA). La integración de la IA en el ámbito educativo ha traído consigo oportunidades y desafíos que requieren una adaptación rápida por parte de los docentes y los sistemas de enseñanza.

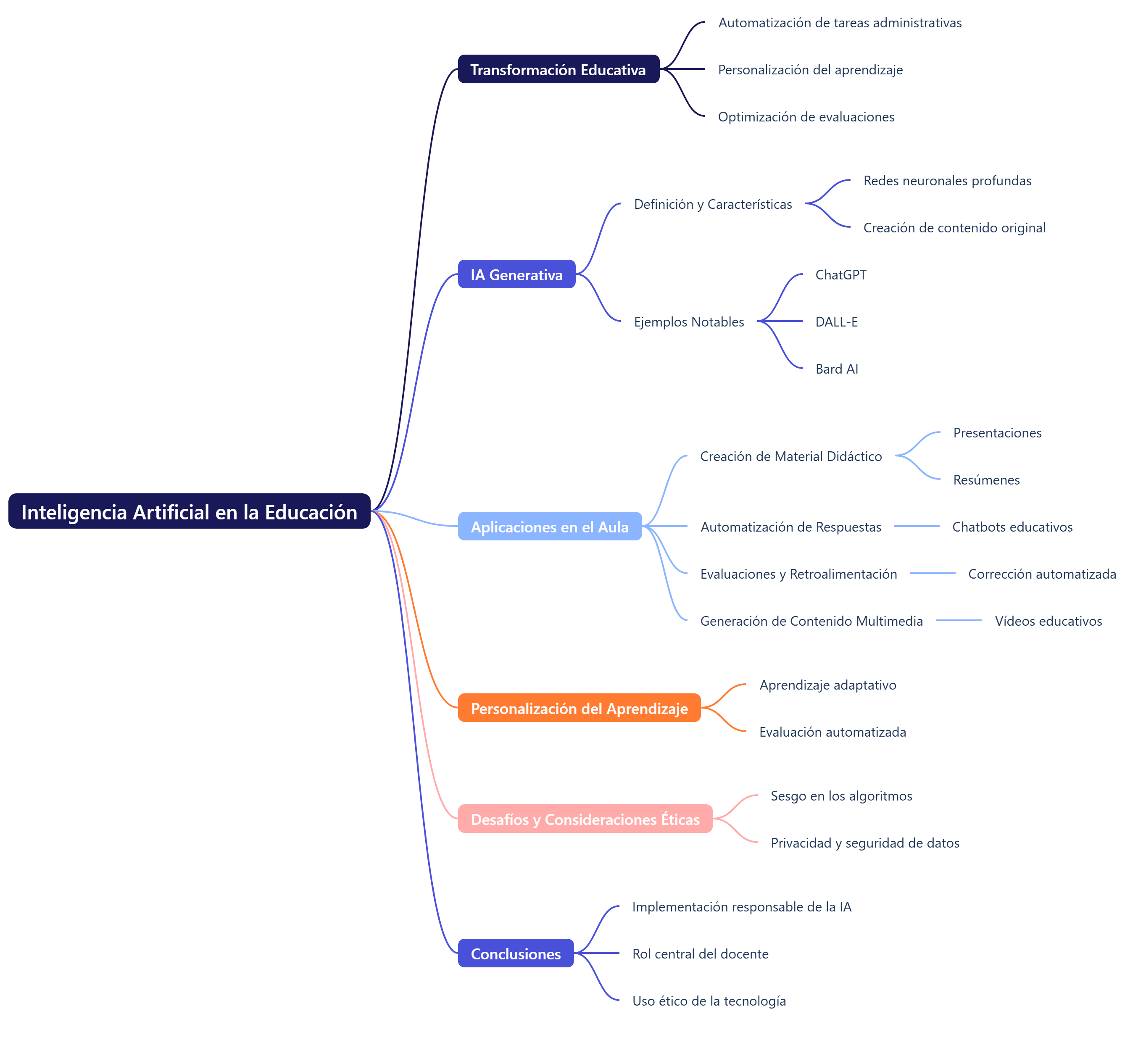
Esta revolución tecnológica ha dado lugar a la automatización de tareas administrativas, la personalización del aprendizaje, la optimización de evaluaciones y el desarrollo de nuevas metodologías de enseñanza que mejoran la eficiencia del aula. Sin embargo, su implementación también genera preocupaciones relacionadas con la equidad, la privacidad de los datos y la ética en la educación.

Este informe explora en profundidad cómo los docentes pueden aprovechar la IA para mejorar sus prácticas pedagógicas y hacer frente a los desafíos emergentes. Se proporcionarán ejemplos detallados, herramientas específicas y estrategias que permitirán a los educadores integrar esta tecnología de manera efectiva y responsable en sus aulas.

1. Inteligencia artificial generativa y su aplicación en la docencia

1.1. Definición y características

La inteligencia artificial generativa es una rama avanzada de la IA que emplea redes neuronales profundas para crear contenido original en formato de texto, imágenes, audio y vídeo. Este tipo de IA puede proporcionar respuestas personalizadas y adaptadas a distintos contextos de aprendizaje, lo que la convierte en una herramienta muy útil en el ámbito educativo.

Algunos ejemplos notables de IA generativa son ChatGPT, que puede generar respuestas detalladas en múltiples idiomas; DALL-E, que crea imágenes a partir de descripciones textuales, y Bard AI, que ofrece información en tiempo real a partir de consultas específicas.

El uso de estas herramientas en la docencia permite mejorar la interacción con los estudiantes, proporcionar materiales personalizados y fomentar un aprendizaje más dinámico. Además, la IA generativa puede ayudar en la corrección de textos, la generación de pruebas automatizadas y la creación de contenidos visuales para reforzar los conceptos enseñados en el aula.

1.2. Aplicaciones en el aula

Las aplicaciones de la inteligencia artificial (IA) generativa en la enseñanza son diversas y pueden utilizarse en diferentes áreas del conocimiento. Entre las más destacadas se encuentran:

Creación de material didáctico: la IA permite generar rápidamente presentaciones, resúmenes y documentos de apoyo para los estudiantes. Herramientas como Canva AI o Tome AI facilitan la producción de diapositivas atractivas con contenido relevante.
Automatización de respuestas: los docentes pueden utilizar chatbots educativos como PersonalChat para responder de manera inmediata a las dudas recurrentes de los estudiantes.
Evaluaciones y retroalimentación: plataformas como Gradescope permiten corregir exámenes de manera automatizada, lo que reduce la carga de trabajo de los docentes y asegura una evaluación más objetiva.
Generación de contenido multimedia: con herramientas como Runway AI y Pictory, los docentes pueden crear vídeos educativos personalizados y mejorar la experiencia de aprendizaje.

Un ejemplo concreto de su aplicación es el uso de ChatGPT en universidades para ayudar a los estudiantes en la redacción de ensayos, proporcionando estructuras sugeridas y correcciones gramaticales detalladas. Esto no solo mejora la calidad de los trabajos académicos, sino que también fomenta la autonomía y la autoevaluación de los estudiantes.

2. Personalización del aprendizaje y evaluación con IA

2.1. Aprendizaje adaptativo

Uno de los mayores beneficios de la inteligencia artificial (IA) en la educación es su capacidad para personalizar el aprendizaje en función del nivel y el ritmo de cada estudiante. Gracias al análisis de datos, los algoritmos de IA pueden identificar fortalezas y debilidades de los alumnos y ajustar los contenidos educativos en tiempo real para optimizar su rendimiento académico.

Algunas plataformas que utilizan este enfoque son:

Khan Academy con IA ofrece ejercicios personalizados según el nivel de conocimiento del estudiante.
Duolingo AI: adapta la dificultad de los ejercicios de idiomas en función del progreso del usuario.
Carnegie Learning ofrece tutorías de matemáticas con IA, que adaptan las preguntas al rendimiento del estudiante.

Este enfoque permite que los estudiantes reciban una educación más centrada en sus necesidades individuales, lo que reduce las brechas de aprendizaje y mejora la retención del conocimiento.

2.2. Evaluación automatizada

Otro aspecto crucial de la IA en la educación es la optimización del proceso de evaluación. Tradicionalmente, corregir exámenes y tareas supone un gran esfuerzo para los docentes. Gracias a herramientas como Gradescope y ZipGrade, ahora es posible evaluar pruebas de manera instantánea, proporcionar retroalimentación detallada y reducir el margen de error.

Además de la corrección automatizada, la IA puede utilizarse para analizar el rendimiento de los estudiantes a lo largo del tiempo y predecir posibles dificultades académicas. Por ejemplo, la plataforma Edsight AI recopila datos sobre las respuestas de los alumnos y genera informes personalizados con recomendaciones para mejorar su rendimiento.

A pesar de sus ventajas, la evaluación automatizada debe complementarse con métodos tradicionales para garantizar una comprensión profunda de los conceptos por parte de los estudiantes y evitar depender exclusivamente de algoritmos para medir los conocimientos.

3. Desafíos y consideraciones éticas

3.1. Sesgo en los algoritmos

Uno de los principales desafíos de la IA en la educación es la presencia de sesgos en los modelos de aprendizaje. Dado que las IA se entrenan con grandes volúmenes de datos históricos, pueden reflejar prejuicios existentes en la sociedad, lo que podría afectar negativamente a la equidad de la enseñanza.

Para minimizar estos riesgos, es fundamental que los docentes supervisen el contenido generado por IA y utilicen diversas fuentes para contrastar la información. Además, se recomienda fomentar el pensamiento crítico entre los estudiantes para que evalúen la veracidad y la imparcialidad de los datos proporcionados por estos sistemas.

3.2. Privacidad y seguridad de datos

El uso de la IA en la educación implica la recopilación y el análisis de grandes volúmenes de datos sobre los estudiantes. Para proteger su privacidad, es crucial que las instituciones educativas implementen regulaciones estrictas sobre el almacenamiento y uso de la información personal.

Algunas estrategias recomendadas son:

Utilización de plataformas con altos estándares de seguridad, como Microsoft Copilot y Google AI Education.
Concienciar sobre la importancia de la privacidad y enseñar a los estudiantes a gestionar sus datos de forma segura en entornos digitales.
Cumplimiento de normativas de protección de datos, como el Reglamento General de Protección de Datos (RGPD) en Europa.

Conclusiones

La inteligencia artificial está revolucionando la educación, ya que ofrece nuevas posibilidades para mejorar la enseñanza y el aprendizaje. Sin embargo, su implementación debe realizarse de manera responsable, garantizando el papel central del docente y promoviendo el uso ético de la tecnología.

Para maximizar sus beneficios, es esencial que los educadores se mantengan actualizados sobre las últimas tendencias en IA y adopten herramientas que complementen sus metodologías de enseñanza. La combinación de innovación tecnológica con estrategias pedagógicas efectivas transformará la educación y preparará a los estudiantes para los desafíos del futuro.

Os dejo un documento de la Universidad de Burgos que profundiza en el tema. Espero que os resulte de interés.

Pincha aquí para descargar

¿Cuál es el mejor algoritmo para optimizar un problema? «No free lunch»

Figura 1. Desgraciadamente, no existe la comida gratis. https://medium.com/@LeonFedden/the-no-free-lunch-theorem-62ae2c3ed10c

Después de años impartiendo docencia en asignaturas relacionadas con la optimización heurística de estructuras de hormigón, y tras muchos artículos científicos publicados y más donde he sido revisor de artículos de otros grupos de investigación, siempre se plantea la misma pregunta: De todos los algoritmos que utilizamos para optimizar, ¿cuál es el mejor? ¿Por qué dice en su artículo que su algoritmo es el mejor para este problema? ¿Por qué no nos ponemos de acuerdo?

Para resolver esta cuestión, dos investigadores norteamericanos, David Wolpert y William Macready, publicaron un artículo en 1997 donde establecieron un teorema denominado «No free lunch«, que traducido sería algo así como «no hay comida gratis». Dicho teorema establece que, por cada par de algoritmos de búsqueda, hay tantos problemas en el que el primer algoritmo es mejor que el segundo como problemas en el que el segundo algoritmo es mejor que el primero.

Este teorema revolucionó la forma de entender el rendimiento de los algoritmos. Incluso una búsqueda aleatoria en el espacio de soluciones podría dar mejores resultados que cualquier algoritmo de búsqueda. La conclusión es que no existe un algoritmo que sea universalmente mejor que los demás, pues siempre habrá casos donde funcione peor que otros, lo cual significa que todos ellos se comportarán igual de bien (o de mal) en promedio.

De hecho, se podría decir que un experto en algoritmos genéticos podría diseñar un algoritmo genético más eficiente que, por ejemplo, un recocido simulado, y viceversa. Aquí el arte y la experiencia en un problema y en una familia de algoritmos determinados, suele ser decisivo. En la Figura 2 se puede ver cómo un algoritmo muy especializado, que conoce bien el problema, puede mejorar su rendimiento, pero pierde la generalidad de poder usarse en cualquier tipo de problema de optimización que no sea para el que se diseñó.

Figura 2. El uso del conocimiento del problema puede mejorar el rendimiento, a costa de la generalidad. https://medium.com/@LeonFedden/the-no-free-lunch-theorem-62ae2c3ed10c

¿Qué consecuencias obtenemos de este teorema? Lo primero, una gran decepción, pues hay que abandonar la idea del algoritmo inteligente capaz de optimizar cualquier problema. Lo segundo, que es necesario incorporar en el algoritmo cierto conocimiento específico del problema, lo cual equivale a una «carrera armamentística» para cada problema de optimización. Se escriben y escribirán miles de artículos científicos donde un investigador demuestre que su algoritmo es mejor que otro para un determinado problema.

Una forma de resolver este asunto de incorporar conocimiento específico del problema es el uso de la inteligencia artificial en ayuda de las metaheurísticas. Nuestro grupo de investigación está abriendo puertas en este sentido, incorporando «deep learning» en el diseño de los algoritmos (Yepes et al., 2020; García et al., 2020a; 2020b), o bien redes neuronales (García-Segura et al., 2017). Incluso, en este momento, me encuentro como editor de un número especial de la revista Mathematics (primer decil del JCR) denominado: “Deep Learning and Hybrid-Metaheuristics: Novel Engineering Applications”, al cual os invito a enviar vuestros trabajos de investigación.

Si nos centramos en un tipo de problema determinado, por ejemplo, la optimización de estructuras (puentes, pórticos de edificación, muros, etc.), el teorema nos indica que necesitamos gente formada y creativa para optimizar el problema concreto al que nos enfrentamos. Es por ello que no existen programas comerciales eficientes capaces de adaptarse a cualquier estructura para optimizarla. Tampoco son eficientes las herramientas generales «tools» que ofrecen algunos programas como Matlab para su uso inmediato e indiscriminado.

Por tanto, no se podrá elegir entre dos algoritmos solo basándose en lo bien que trabajaron anteriormente en un problema determinado, pues en el siguiente problema pueden optimizar de forma deficiente. Por tanto, se exige conocimiento intrínseco de cada problema para optimizarlo. Es por ello que, por ejemplo, un experto matemático o informático no puede, sin más, dedicarse a optimizar puentes atirantados.

Referencias:

GARCÍA, J.; YEPES, V.; MARTÍ, J.V. (2020a). A hybrid k-means cuckoo search algorithm applied to the counterfort retaining walls problem. Mathematics, 8(4), 555.

GARCÍA, J.; MARTÍ, J.V.; YEPES, V. (2020b). The buttressed walls problem: An application of a hybrid clustering particle swarm optimization algorithm. Mathematics, 8(6):862.

GARCÍA-SEGURA, T.; YEPES, V.; FRANGOPOL, D.M. (2017). Multi-Objective Design of Post-Tensioned Concrete Road Bridges Using Artificial Neural Networks. Structural and Multidisciplinary Optimization, 56(1):139-150.

WOLPERT, D.H.; MACREADY, W.G. (1997). No Free Lunch Theorems for Optimization. IEEE Transactions on Evolutionary Computation, 1(1):67-82.

YEPES, V.; MARTÍ, J.V.; GARCÍA, J. (2020). Black hole algorithm for sustainable design of counterfort retaining walls. Sustainability, 12(7), 2767.

A continuación os dejo el artículo original «No Free Lunch Theorems for Optimization». Se ha convertido en un clásico en optimización heurística.

Pincha aquí para descargar

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Comunicaciones presentadas al congreso MAEB 2015

A continuación vamos a presentar brevemente los resúmenes que enviamos al Congreso Nacional sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados (MAEB). Este Congreso pretende ser un foro de encuentro, discusión y transferencia de conocimiento entre investigadores en el campo de las metaheurísticas y los algoritmos bioinspirados, con el fin de presentar e intercambiar experiencias y resultados.

La X edición, MAEB’2015, se celebrará en Mérida-Almendralejo, durante los días 4 al 6 de Febrero de 2015, y está organizada por el Centro Universitario de Mérida perteneciente a la Universidad de Extremadura. Las áreas temáticas integradas en el congreso incluyen estudios teóricos, aplicaciones prácticas, experiencias docentes y desarrollos en el campo de investigación en optimización heurística (información detallada en el apartado de llamada a la participación). Los autores agradecen el aporte financiero realizado para este trabajo por el Ministerio de Ciencia e Innovación (Proyecto de Investigación BIA2011-23602) y por la Universitat Politècnica de València (Proyecto de Investigación SP20120341).

GARCÍA-SEGURA, T.; YEPES, V.; MARTÍ, J.V.; ALCALÁ, J. (2015). Algoritmo híbrido de enjambre de luciérnagas y aceptación por umbrales para diseño de vigas. X Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados – MAEB 2015, 4-6 de febrero, Mérida.

Este estudio convierte el diseño estructural en una optimización de variables discretas. Se propone un algoritmo híbrido de enjambre de luciérnagas para buscar soluciones con menores emisiones totales y anuales. El algoritmo combina la búsqueda colectiva de la optimización de enjambre luciérnagas “glowworm swarm optimization“(GSO) y la capacidad de búsqueda local del umbral de aceptación “threshold accepting” (TA). La estructura propuesta es una viga de hormigón en doble T biapoyada definida por 20 variables. Se estudia la resistencia del hormigón desde 30MPa hasta 100MPa. Esta comunicación propone un método para calibrar los parámetros del algoritmo con independencia de la función objetivo y del tamaño del enjambre. Los resultados muestran que TAGSO consigue diseños de vigas que emiten un 25% menos de CO₂. La optimización de las emisiones anuales reduce la cantidad de CO₂ al año en un 61% con un incremento total de las emisiones de CO₂ del 9%.

MARTÍ, J.V.; YEPES, V.; GARCÍA-SEGURA, T. (2015). Aplicación de metaheurísticas en la optimización de pasos superiores de carreteras. X Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados – MAEB 2015, 4-6 de febrero, Mérida.

El artículo se ocupa de la optimización económica de los tableros de los pasos superiores de carreteras formados por una losa de hormigón ejecutada in situ y dos vigas artesa prefabricadas de hormigón pretensado autocompactable. Se comprueba la eficacia de las distintas metaheurísticas aplicadas en la optimización: “descent local search” (DLS), “simulated annealing” (SA), “threshold accepting” (TA), “genetic algoritms” (GA) y “memetic algorithms” (MA). Los cálculos de las tensiones y de sus envolventes, son programados en lenguaje fortran directamente por los autores. Los algoritmos de optimización heurística se aplican a un tablero de 35 m de luz y 12 m de ancho. Los parámetros que definen la forma de la sección de la viga se adaptan a los moldes de una instalación de prefabricados. El ejemplo que se analiza consta de 59 variables discretas. El módulo de la evaluación incluye los estados límite último y de servicio que se aplican comúnmente para estas estructuras: flexión, cortante, torsor, fisuración, flechas, etc. Los algoritmos SA y TA se han calibrado previamente a partir del DLS, y el MA a partir del GA y del SA. Cada heurística se procesa nueve veces, obteniéndose información estadística sobre el valor mínimo, el medio y las desviaciones. Se realiza un análisis del rendimiento de las distintas heurísticas, basado en un estudio de las soluciones Pareto-óptimas entre tiempo de ejecución y rendimiento. Los mejores resultados se obtienen para el SA y el TA, siendo el coste mínimo de 108008 €, correspondiente al SA. Finalmente, entre las principales conclusiones de este estudio, destaca que las soluciones y los tiempos de proceso computacional son tales, que estos métodos se pueden aplicar de un modo práctico a casos reales, y que el conocimiento derivado del uso de estos algoritmos permiten recomendar rangos de valores para emplearlos en el diseño optimizado de estas estructuras y en su aplicación para los predimensionados de las variables.

YEPES, V.; MARTÍ, J.V. (2015). Teoría del valor extremo como criterio de parada en la optimización heurística de puentes. X Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados – MAEB 2015, 4-6 de febrero, Mérida.

El artículo establece un criterio de parada para un algoritmo multiarranque basado en el recocido simulado aplicado a la optimización de losas de puentes de vigas prefabricadas de hormigón pretensado. Para ello se ha comprobado que los óptimos locales encontrados constituyen valores extremos que ajustan a una función Weibull de tres parámetros, siendo el de posición, γ, una estimación del óptimo global que puede alcanzar el algoritmo. Se puede estimar un intervalo de confianza para γ ajustando una distribución Weibull a muestras de óptimos locales extraídas mediante una técnica bootstrap de los óptimos disponibles. El algoritmo multiarranque se detendrá cuando se acote el intervalo de confianza y la diferencia entre el menor coste encontrado y el teórico ajustado a dicha función Weibull.