¿Por qué son tan complicados los problemas de distribución física?

Los problemas de distribución física consisten básicamente en asignar una ruta a cada vehículo de una flota para repartir o recoger mercancías. Los clientes se localizan en puntos o arcos y a su vez pueden presentar horarios de servicio determinados; el problema consiste en establecer secuencias de clientes y programar los horarios de los vehículos de manera óptima. Los problemas reales de transporte son extraordinariamente variados. Yepes (2002) propone una clasificación que contiene un mínimo de 8,8·10⁹ combinaciones posibles de modelos de distribución. Si alguien fuese capaz de describir en un segundo cada uno de ellos, tardaría cerca de 280 años en enunciarlos todos. La investigación científica se ha centrado, por tanto, en un grupo muy reducido de modelos teóricos que además tienden a simplificar excesivamente los problemas reales. Son típicos problemas de optimización matemática combinatoria.

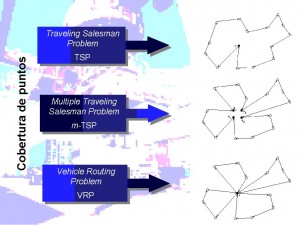
El problema más famoso y sencillo de plantear se conoce como el del viajante de comercio (“Traveling Salesman Problem”, TSP). Se debe visitar un conjunto de ciudades una sola vez y volver a la ciudad de partida, de modo que la distancia recorrida sea mínima. Es un problema intensivo en términos de cálculo, puesto que un procesador que calculara un billón de soluciones por segundo tardaría unos 50 minutos en enumerar todos los casos posibles con 20 nodos y casi cinco siglos con el de 25.

El problema de las rutas “Vehicle Routing Problem, VRP” presenta una demanda asociada a cada ciudad y una capacidad determinada de transporte para cada uno de los vehículos. Aquí, el objetivo puede ser reducir al mínimo posible la suma de la distancia recorrida por todas las rutas, el número de vehículos, o una combinación de ambos criterios. Es importante destacar el hecho de que tanto para los problemas TSP como para los VRP, la dirección en la cual se desarrolla el camino carece de importancia, cosa que no ocurre con los problemas de rutas de reparto con restricciones en los horarios de servicio “Vehicle Routing Problem with Time Windows, VRPTW”, donde cada cliente restringe la satisfacción de su demanda a un horario de reparto o recogida determinado (ventana de tiempo). En estos casos, la ventana de tiempo obliga a una espera si el vehículo llega antes de su apertura, e impide la realización del servicio si se llega fuera del plazo previsto. La Tabla 1 recoge algunos ejemplos de aplicaciones prácticas.

Tabla 1. Ejemplos de aplicaciones reales del problema VRPTW.

Estos problemas son difíciles de resolver debido al crecimiento exponencial de soluciones en relación con el número de clientes. De hecho, sólo algunos problemas VRPTW de hasta 100 nodos han podido calcularse mediante métodos exactos. En estas circunstancias, es posible aplicar algoritmos de aproximación que proporcionen soluciones viables que sean razonables.

Referencias

YEPES, V. (2002). Optimización heurística económica aplicada a las redes de transporte del tipo VRPTW. Tesis Doctoral. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Universitat Politècnica de València. 352 pp. ISBN: 0-493-91360-2. (pdf)

YEPES, V.; MEDINA, J.R. (2003). Optimización económica de redes de transporte del tipo VRPTW. Revista de Obras Públicas, 3436: 31-39. Octubre. Depósito Legal: M-156-1958. ISSN: 0034-8619. Edita: Colegio de Ingenieros de Caminos, Canales y Puertos. Madrid. (pdf)