Adhémar Jean Claude Barré de Saint-Venant (Villiers-en-Bière, Seine-et-Marne, Francia, 23 de agosto de 1797 – Saint-Ouen, Loir-et-Cher, Francia, enero de 1886) fue un ingeniero, matemático y científico de la mecánica de medios continuos francés que contribuyó de manera decisiva al nacimiento de esta disciplina, tanto en la mecánica de sólidos deformables como en la mecánica de fluidos. Aunque su apellido completo era Barré de Saint-Venant, en la bibliografía no francesa suele aparecer simplemente como Saint-Venant.
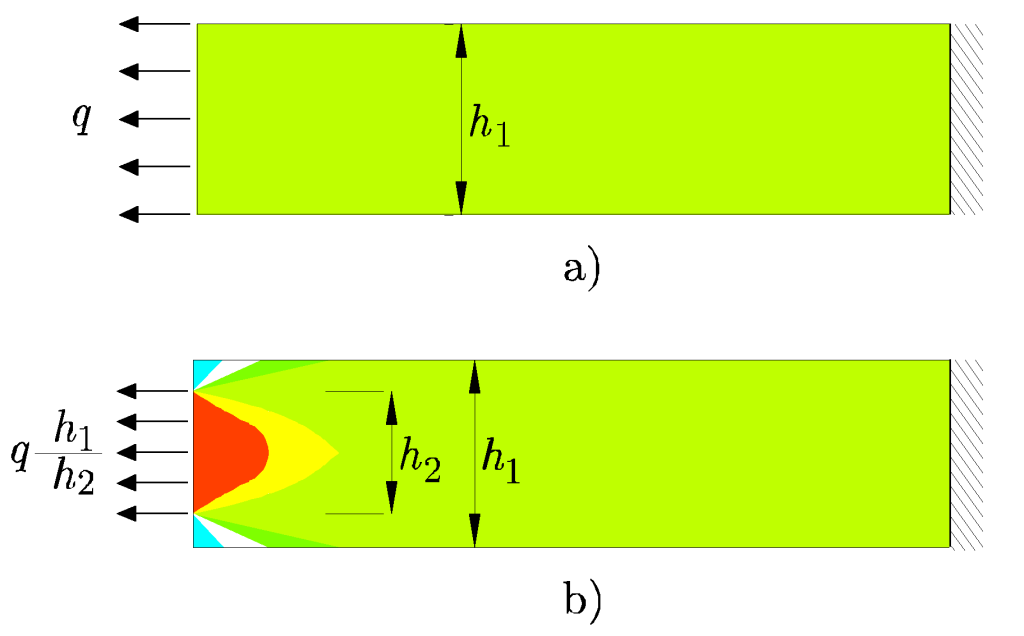
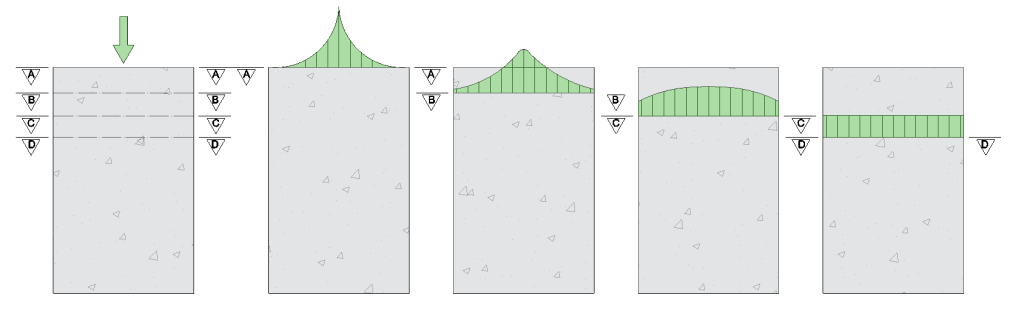
Fue un pionero en el estudio de los esfuerzos en estructuras. Su nombre está vinculado al principio de Saint-Venant para sistemas de cargas equivalentes, al teorema de Saint-Venant, que establece que el círculo es la sección maciza más efectiva contra la torsión, y a la condición de compatibilidad de Saint-Venant, que garantiza la integrabilidad de los tensores de deformación. En mecánica de fluidos, desarrolló las ecuaciones que describen el flujo unidimensional no estacionario de un fluido en lámina libre para aguas poco profundas, conocidas como ecuaciones de Saint-Venant. También fue el primero en «identificar adecuadamente el coeficiente de viscosidad y su papel como factor multiplicador de los gradientes de velocidad en un flujo».
Además, desarrolló un cálculo vectorial similar al de Grassmann (hoy considerado una forma de cálculo exterior), que publicó en 1845. Esto dio lugar a una disputa sobre la prioridad con Grassmann, quien había publicado sus resultados un año antes, en 1844, aunque Saint-Venant afirmó haber ideado el cálculo en 1832.
Vida
Nació el 23 de agosto de 1797 en el Château de Fortoiseau, en Villiers-en-Bière (Seine-et-Marne). Su padre, Jean Barré de Saint-Venant (1737-1810), fue oficial colonial en la isla de Santo Domingo y su madre, Marie-Thérèse Josèphe Laborie, nació en Haití en 1769.
En 1813, con tan solo dieciséis años, ingresó en la École Polytechnique, donde estudió bajo la dirección de Gay-Lussac. Ese mismo año, París se preparaba para resistir la invasión tras la derrota de Napoleón en Leipzig. Todos los estudiantes fueron movilizados, pero Saint-Venant se negó a combatir diciendo: «Mi conciencia me prohíbe luchar por un usurpador». Por esta negativa, tuvo que abandonar la escuela. No obstante, en 1816 logró graduarse como ingeniero tras completar los estudios interrumpidos.
A partir de ese momento, trabajó como ingeniero durante 27 años. Inicialmente, su afición por la química le llevó a ser élève-commissaire del Service des Poudres et Salpêtres (Servicio de Pólvoras y Nitratos), donde trabajó durante los primeros siete años. Posteriormente, durante los veinte años siguientes, ejerció como ingeniero civil en el Corps des Ponts et Chaussées (Cuerpo de Puentes y Caminos). Al mismo tiempo, asistió a cursos en el Collège de France y todavía se conservan sus detalladas notas de las clases de Liouville de 1839-1840.
En 1823 obtuvo permiso para reincorporarse formalmente a la École des Ponts et Chaussées, donde se graduó en 1825 y llegó a ser ingeniero jefe de segunda clase. En 1837 se casó con Rohaut Fleury, de París. Tras un desacuerdo con la administración municipal, se retiró del servicio público el 1 de abril de 1848.
En 1850 ganó por concurso la cátedra de ingeniería agronómica en el Instituto Agronómico de Versalles, que ocupó durante dos años. En ese contexto, en 1851 publicó Principes de Mécanique fondés sur la Cinématique, donde defendía una concepción atomista de la materia y presentaba las fuerzas como entidades cinemáticas, desligadas de las nociones metafísicas o fisiológicas que, en su opinión, oscurecían el concepto físico de fuerza. Su uso del cálculo vectorial, introducido en estas lecciones, fue adoptado por el sistema escolar francés. Posteriormente, sucedió a Coriolis como profesor de matemáticas en la École des Ponts et Chaussées.
En 1868, con 71 años, fue elegido para ocupar la plaza de la sección de Mecánica de la Academia de Ciencias de Francia, en sustitución de Poncelet. En 1869, el papa Pío IX le concedió el título de conde. En 1883, a los 86 años, tradujo (junto con A. Flamant) al francés la Théorie de l’élasticité des corps solides de Clebsch, añadiendo él mismo notas originales al texto. Flamant también redactó su necrológica oficial con otros colegas.
Saint-Venant murió en enero de 1886 en Saint-Ouen (Loir-et-Cher). Las fuentes discrepan sobre la fecha exacta: algunas señalan el 6 de enero y otras el 22.
Obra científica
Saint-Venant trabajó principalmente en mecánica, elasticidad, hidrostática e hidrodinámica. Fue uno de los primeros en aplicar rigurosamente el concepto de esfuerzos internos en sólidos y en describir las condiciones para la integrabilidad de los campos de deformación. En la década de 1850, desarrolló soluciones para la torsión de cilindros no circulares y amplió el trabajo de Navier sobre la flexión de vigas, publicando en 1864 un tratado exhaustivo sobre el tema.
Su contribución más destacada fue probablemente su trabajo de 1843, en el que redescubrió correctamente las ecuaciones de Navier-Stokes para flujos viscosos. En palabras de Anderson:
Siete años después de la muerte de Navier, Saint-Venant rederivó sus ecuaciones para un flujo viscoso, considerando las tensiones internas viscosas y descartando por completo el enfoque molecular de Navier. Su artículo de 1843 fue el primero en identificar adecuadamente el coeficiente de viscosidad y su papel como factor que multiplica los gradientes de velocidad en el flujo, interpretando estos productos como tensiones viscosas debidas a la fricción interna. Saint-Venant lo hizo bien y lo documentó. Que su nombre no quedara asociado a estas ecuaciones es un misterio, sin duda una injusticia técnica.
Stokes también las derivó correctamente, pero su publicación se produjo dos años más tarde, en 1845.
En el ámbito de la hidrodinámica, desarrolló las ecuaciones para el flujo no estacionario en lámina libre, que hoy llevan su nombre (ecuaciones de Saint-Venant). En 1871, derivó las ecuaciones para el flujo no estacionario en canales abiertos.
En 1845, publicó una versión del cálculo vectorial similar a la de Grassmann, quien había publicado en 1844. Saint-Venant defendió que ya había desarrollado estas ideas en 1832 y utilizó este cálculo vectorial en sus clases en el Instituto Agronómico y en su obra de 1851. Aunque sus concepciones atomistas no prosperaron, su enfoque vectorial se adoptó en la enseñanza francesa.
Saint-Venant es recordado como un ingeniero, matemático y científico mecánico excepcional, pionero de la mecánica de medios continuos, del estudio del esfuerzo y la deformación en estructuras, de la hidrodinámica y del cálculo vectorial. Sus contribuciones fundamentales a la elasticidad, los flujos viscosos, la torsión de estructuras y el cálculo cinemático lo sitúan como uno de los grandes fundadores de la ingeniería y la mecánica moderna.