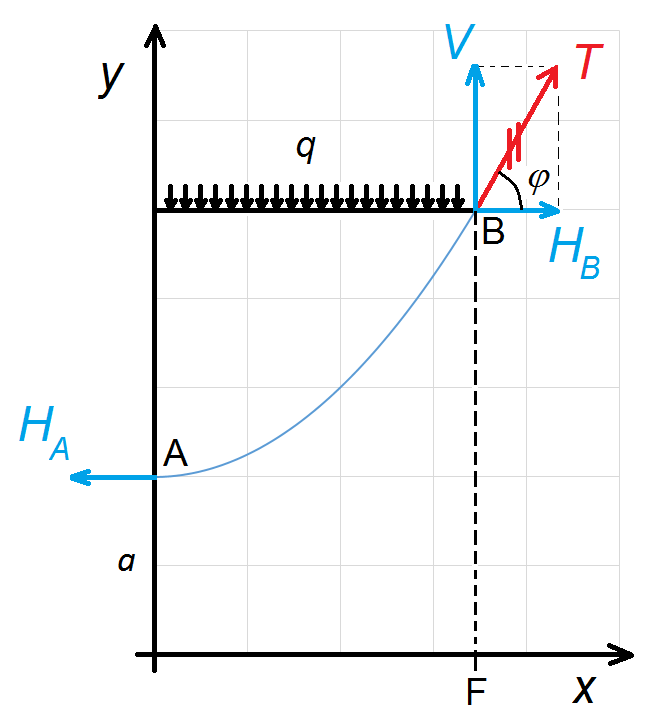
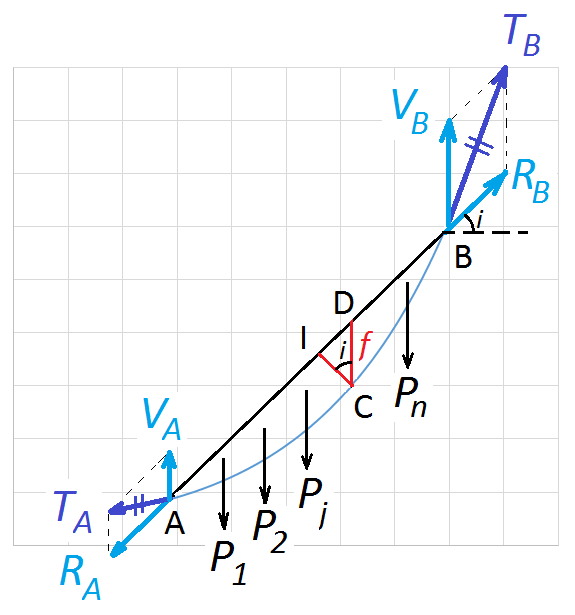
A continuación se deduce la ecuación fundamental de la estática de los cables. Para ello suponemos un cable infinitamente flexible, sometido a la acción de su peso propio y a una serie de cargas verticales aisladas, diferentes y distribuidas de un modo cualquiera (tal y como vemos en la figura).
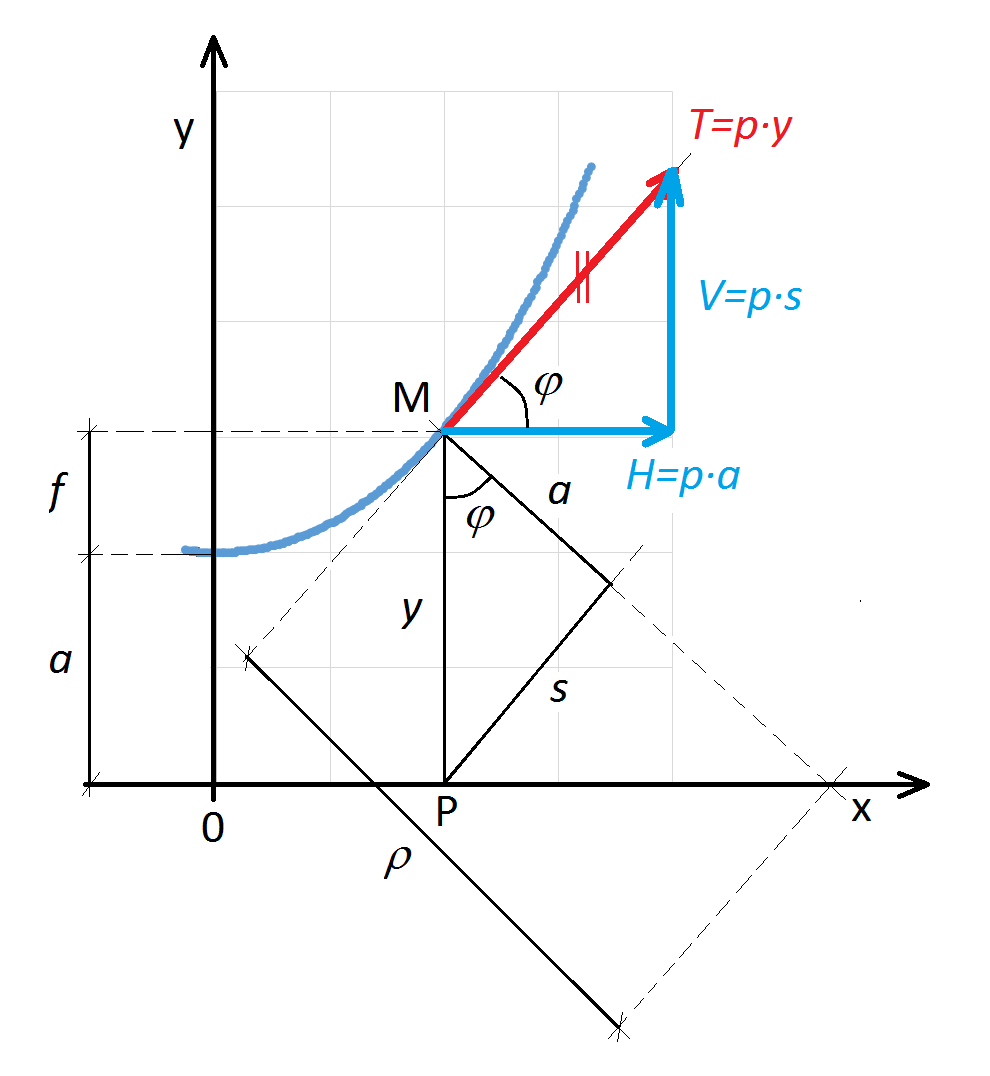
Esta ecuación demuestra que la distancia de un punto del cable a la cuerda que une dos puntos cualesquiera se puede calcular como el cociente entre el momento isostático de todas las fuerzas situadas a la derecha (o a la izquierda) de dicho punto y la tensión horizontal del cable.
Veamos a continuación la demostración de esta ecuación.
