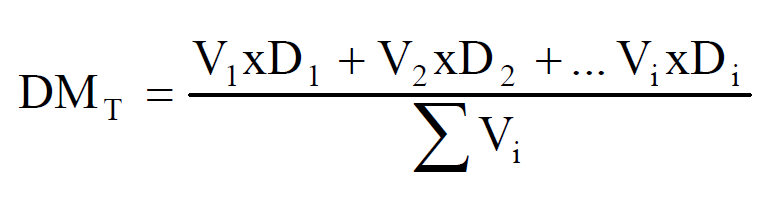El diagrama de masas de Bruckner permite la optimización del transporte en el movimiento de tierras. De este tema ya hicimos un artículo anterior que os recomiendo repasar. En este vamos a centrarnos más en el proceso de cálculo.
Este tema y ejercicios resueltos son algunos casos que se explican dentro del Curso de gestión de costes y producción de la maquinaria empleada en la construcción. Os animo a que, si estáis interesados, os informéis de este curso en línea.
Volviendo al contenido de este artículo, se trata de determinar los volúmenes a transportar, las distancias de acarreo, los vertederos y los préstamos. Este diagrama permite ajustar la compensación longitudinal y las distancias a las que trasladar los volúmenes de desmonte y terraplén (Figura 1).
Entre las propiedades más interesantes del diagrama, se tienen las siguientes:
- La ordenada de un punto cualquiera mide el volumen acumulado desde el origen.
- El volumen excedente acumulado en el origen es nulo, y la horizontal trazada por él, se llama fundamental.
- La curva de volúmenes es ascendente para desmontes y descendente para terraplenes.
- Un máximo o un mínimo de la curva, son puntos de paso entre terraplenes y desmontes.
- La diferencia de ordenadas entre dos puntos mide el volumen a mover entre ambos.
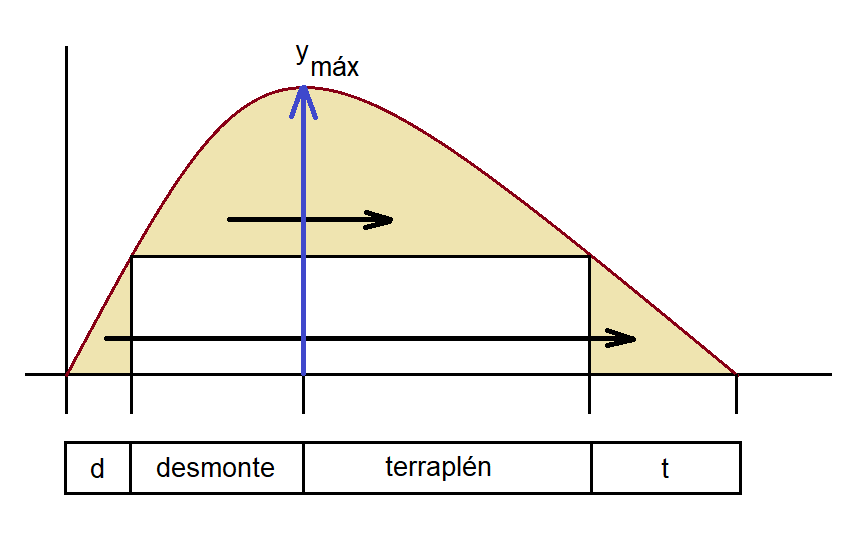
- Entre las secciones correspondientes a los puntos de intersección de una horizontal cualquiera con la curva de volúmenes, existe compensación entre desmonte y terraplén. El volumen total de tierra a transportar está dado por la ordenada máxima del arco de diagrama comprendido, con relación a la horizontal considerada (Figura 2).
- El momento de transporte es el trabajo necesario para mover un volumen de suelo desde su posición original, una vez determinada la distancia, hasta la posición final de proyecto. Es el producto del volumen transportado (ordenada) por la distancia (abscisa).
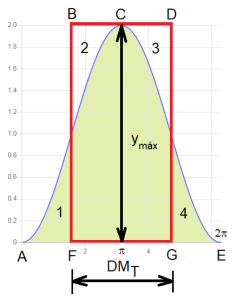
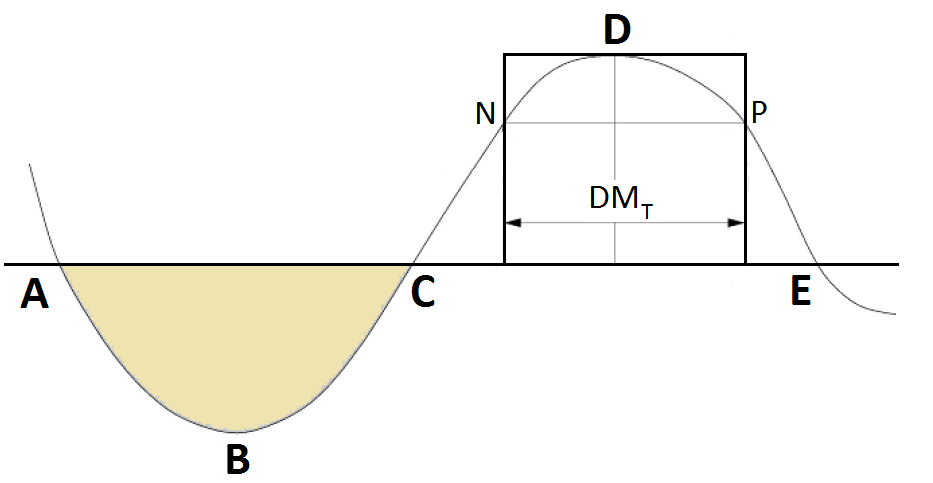
- El área de cada cámara de compensación respecto a una horizontal cualquiera mide el momento de transporte de la compensación entre las secciones correspondientes a la intersección de dicha horizontal con la línea del diagrama. El área dividida por la ordenada máxima es la distancia media de transporte. Existe entonces un rectángulo de área equivalente al área de la onda y que tiene por altura el volumen de tierra a transportar (Figura 3).
- Con respecto a una horizontal cualquiera, las ondas situadas por arriba, con el primer tramo ascendente (exceso de excavación) y el segundo descendente (exceso de terraplén) se llaman “montes”. Asimismo, las situadas por debajo con el primer tramo descendente y el segundo ascendente se llaman “valles”.
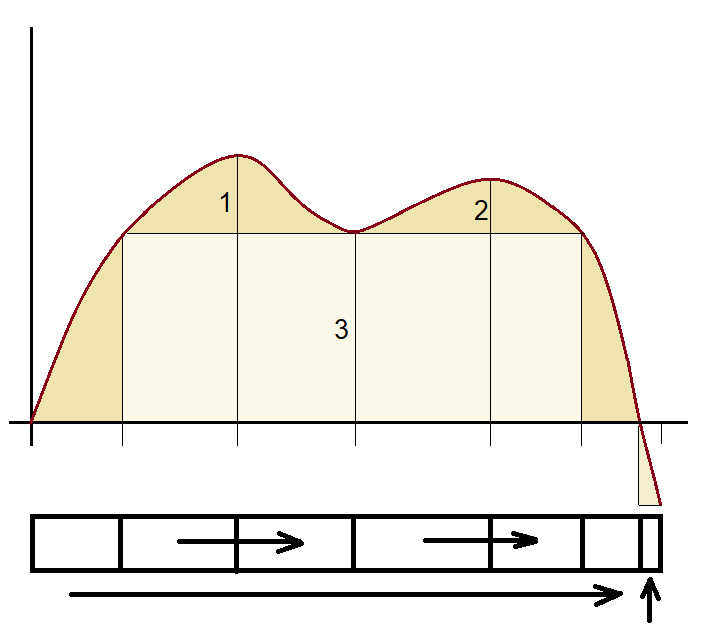
- Para minimizar el coste, en el diagrama la suma de las bases de los valles debe ser igual a la suma de las bases de los montes (Figura 4).

Figura 4. La suma de las longitudes de valles y montes deben ser iguales para minimizar el coste.
Para optimizar el movimiento de tierras, se pueden seguir las denominadas reglas de Corini, que son las siguientes:
- La longitud de distribución estará comprendida entre la fundamental y una horizontal trazada por la sección extrema.
- Se trazarán diversas horizontales de compensación, comprendiendo cada una un monte y un valle de igual base.
- De no ser posible la 2, se trazarán horizontales, en sentido ascendente o descendente, comprendiendo más valles y más montes, de modo que la suma de la base de los montes sea igual a la suma de la base de los valles.
- La horizontal de distribución secundaria (dentro de una cámara autocompensada) debe ser tangente a la onda (Figura 5).
La obtención de las distancias medias de transporte se ha realizado apoyándose en las propiedades de la línea de volúmenes:
- Cálculo de la diferencia entre dos ordenadas con respecto a una horizontal cualquiera. Esta diferencia da el volumen de desmonte o terraplén disponible entre ellas.
- Entre las secciones correspondientes a los puntos de intersección de una horizontal con la línea de volúmenes existe compensación de desmonte y terraplén; el volumen total de tierras a mover entre esas dos secciones será la ordenada máxima con relación a la horizontal considerada.
- Efectuando la compensación por horizontales, la tierra del punto N se arroja en el P, el área de cada cantera de compensación, correspondiente a una horizontal determinada, mide el momento de transporte de la compensación entre las secciones de intersección de la horizontal con la línea de volúmenes. El área ABC (Figura 2) mide el momento de transporte de la compensación entre A y C.
- Los parámetros que intervienen en el cálculo de la distancia media de transporte de las compensaciones longitudinales son, básicamente, los volúmenes parciales y las áreas parciales entre perfiles, con cuya suma se obtiene el volumen transportado y la superficie total de cada área compensada denominada esencialmente cantera de compensación.
- Considerando las propiedades analíticas de los diagramas de masas para la obtención del producto volumen por cada distancia de cada compensación longitudinal, la distancia media de transporte para cada área compensada que delimita el diagrama y el eje de abscisas, será el cociente entre el área y el volumen transportado de la misma.
- Por último, la distancia media de transporte global de la compensación longitudinal se determina con la ponderación de los productos volumen por distancia media de las áreas compensadas existentes dividida por el volumen transportado total.
Referencias:
YEPES, V. (1995). Maquinaria de movimiento de tierras. Servicio de Publicaciones de la Universidad Politécnica de Valencia. SP.UPV-264. 144 pp.
YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.
YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.