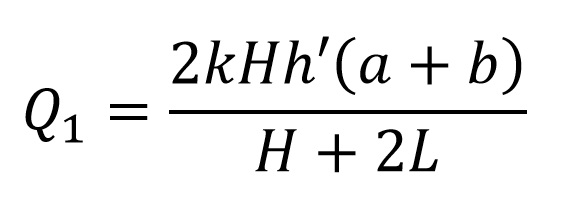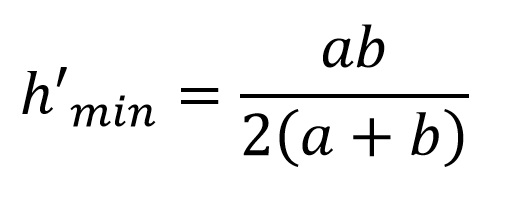Resulta muy habitual en edificación excavar sótanos que se encuentran bajo nivel freático. Esta excavación suele realizarse al abrigo de un recinto de muros o pantallas y se hace necesario drenar el agua que queda al fondo de la excavación. Para un estudio en detalle del flujo hidráulico en un medio poroso deberíamos acudir a la ecuación de Laplace y proceder a la integración de este tipo de ecuación en derivadas parciales atendiendo a las condiciones de contorno. Sin embargo, vamos a dar aquí una solución aproximada que puede servir en obra para efectuar una previsión de las bombas de achique necesarias o tomar decisiones tales como prolongar las pantallas lo suficiente como para empotrarlas en un sustrato impermeable. Como siempre, cada caso es particular y requiere de un estudio económico para ver la mejor opción.
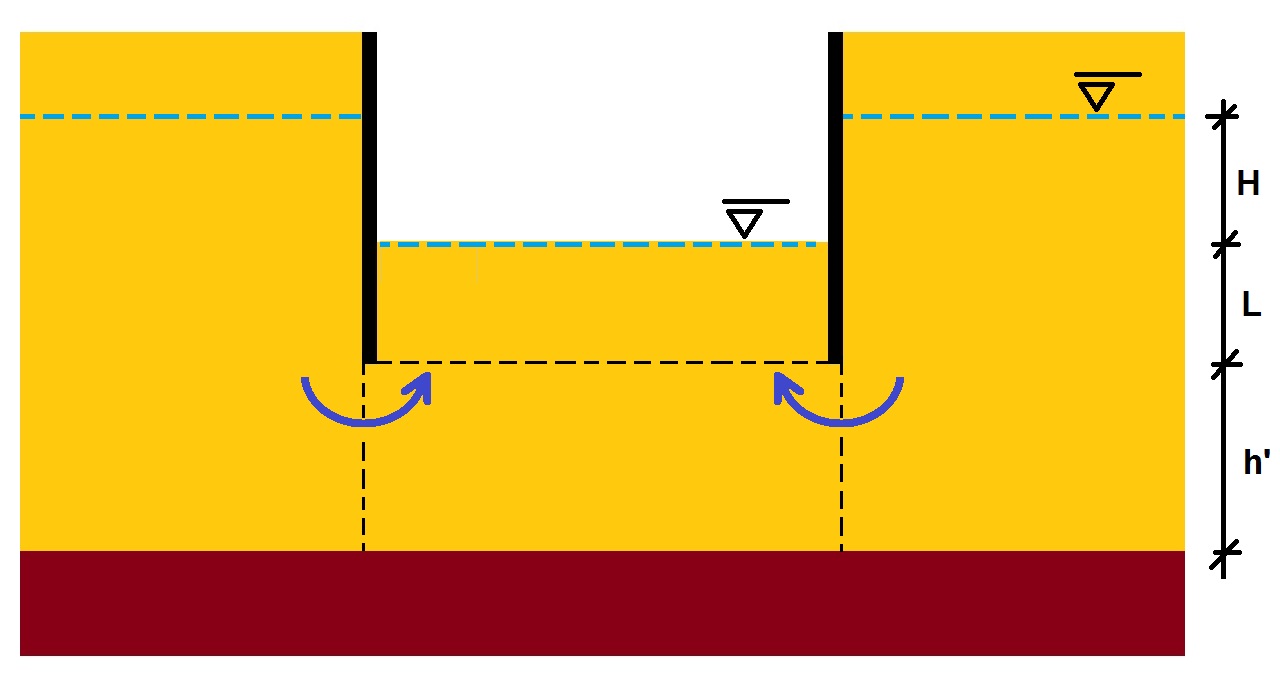
Vamos a suponer que se va a excavar un solar, de dimensiones “a·b” en presencia de nivel freático, en un terreno poroso con un coeficiente de permeabilidad “k“. Las pantallas se encuentran empotradas una longitud “L“, el fondo de excavación se encuentra a una profundidad “H” respecto al nivel freático y existe un estrato impermeable a una distancia “h‘” respecto a la pantalla (ver Figura 2). Se pretende calcular el caudal de achique de forma que el agua no se encharque en el fondo de la excavación. Se supone que se ha realizado una evaluación previa para evitar el sifonamiento, el levantamiento de la excavación y el cálculo mecánico de las pantallas, entre otros aspectos.
Para resolver el problema emplearemos la Ley de Darcy, que establece que la velocidad de un fluido en medio poroso es proporcional al gradiente hidráulico. Multiplicando esa velocidad por la sección que atraviesa el flujo, tendremos la evaluación del caudal según la siguiente expresión, donde “Q” es el caudal, “k” es el coeficiente de permeabilidad”, “i” es el gradiente hidráulico y “S” es la sección atravesada por el flujo.
En el problema que nos ocupa, el caudal puede atravesar dos secciones, una lateral determinada por el estrato impermeable y el fondo de la pantalla “S1”, y la formada por el fondo de la excavación del solar “S2”. Calculemos en ambos casos el caudal. Es posible realizar una estimación aproximada considerando el flujo del agua próximo a la pantalla, puesto que es la línea de flujo más corta y la que supone un mayor gradiente crítico. En este caso, i=H/(H+2L).
Para la sección “S1″, el caudal “Q1″ tendrá el siguiente valor:
Análogamente, para la sección”S2″, el caudal “Q2″ tendrá el siguiente valor:
El caudal estimado será el menor de ambas dos estimaciones: Q=min(Q1, Q2).
Igualando ambos caudales se puede determinar la distancia del sustrato impermeable al fondo de la pantalla a partir de la cual dicho sustrato no influye en la estimación del caudal:
En el caso de un solar cuadrado, si el sustrato impermeable se encuentra a una distancia superior a la cuarta parte del lado del solar, todo el flujo pasa por el fondo de la excavación.
De todas formas, de las expresiones anteriores se deduce que el caudal máximo que puede entrar en la excavación se da cuando el sustrato impermeable se encuentra a una distancia del fondo de la pantalla superior al cociente entre el área y el perímetro del recinto. Si la capa impermeable se encuentra más cerca, el caudal baja proporcionalmente hasta anularse teóricamente cuando llega a tocar a la pantalla.
Os dejo un vídeo explicativo que espero os sea útil.
Referencias:
PÉREZ VALCÁRCEL, J.B. (2004). Excavaciones urbanas y estructuras de contención. Ediciones Cat. Colegio Oficial de Arquitectos de Galicia.
YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.
Curso:

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.