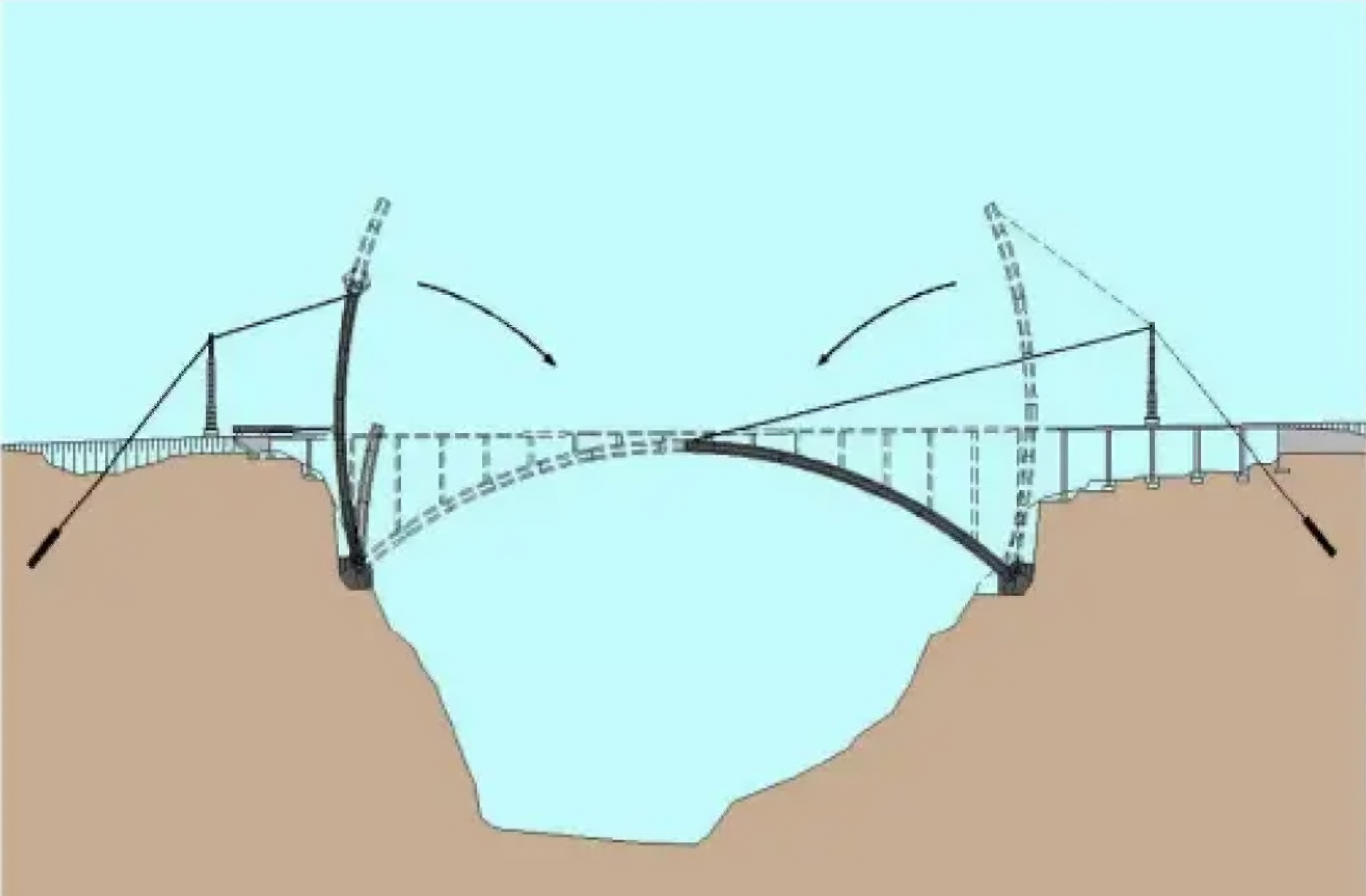
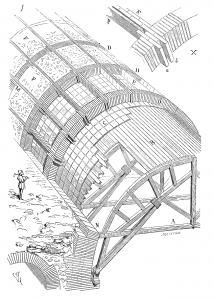
Seguimos con este artículo un repaso histórico de los arcos. Como en su día se dijo, este es un «invento diabólico» que revolucionó en su momento el arte de construir. Vamos, pues a seguir con esta labor divulgadora, a sabiendas que nos dejamos muchas cosas por el camino.
Desde la Roma clásica al Renacimiento, los arcos y los estribos se diseñaban con reglas de buena práctica y con criterios geométricos. Los constructores, desconocedores de las nociones de las fuerzas y sus líneas de acción, tuvieron que utilizar reglas en forma de proporciones o bien hacer modelos. Estos criterios empíricos no deberían ser tan absurdos pues, como indica Huerta (1996), la prueba es que muchas estructuras construidas en la época “pre-científica” -donde se incluyen todas las catedrales góticas-, fueron concebidas de esta forma.
Los secretos del oficio, guardados celosamente por los gremios y transmitidos oralmente, en un lenguaje hermético y oscurantista, empiezan a difundirse con los tratados de Arquitectura a partir del Renacimiento. Diego de Sagredo, Alberti o Palladio encabezan un listado de tratadistas que divulgan el pensamiento arquitectónico renacentista.

Alberti[1] es el primer autor que establece, en 1452, las reglas para conseguir la estabilidad y constructibilidad de un puente de fábrica. Su tratado de arquitectura, De re aedificatoria, fue un compendio del saber constructivo de su época (Huerta, 2000:514). Sin embargo la edición en latín se publicó en 1485 –antes que la primera edición de Vitruvio[2]– y en España no se tradujo hasta 1582. La intuición mecánica de Alberti le sugiere que la forma del arco es la base para valorar su modo de trabajar: “El arco poco curvo es seguro para su propio peso, pero si se carga conviene componer muy bien su trasdós”, o bien: “El arco muy curvado será en sí mismo débil, cuanto más se carga menos problemas tendrá en su trasdós”. Cuanto más apuntado es un arco, es decir, cuanta mayor sensación visual da de no caer, más resistencia se le confiere.
Palladio[3], en su tratado I Quattro Libri dell’Architettura, de 1570, recoge el dimensionamiento de ejemplos de puentes romanos, dándolos como reglas prácticas.
Leonardo da Vinci[4] fue el primero que intentó estudiar los arcos desde el punto de vista mecánico, como muestran numerosos dibujos del Códice de Madrid, aunque sus análisis desconocían la ley del paralelogramo de fuerzas, fundamental en cualquier estudio estático, que no se resolvió hasta 1586 por Stevenin[5] (Heyman, 1999:92), si bien se formula en su forma actual en 1724 por Varignon[6] en su obra Nouvelle mécanicque.

La primera explicación científica del arco tuvo que esperar a Hooke[7], quien en 1676 apuntó que funcionaba justo al revés que un cable colgado, si bien no halló la ecuación matemática de dicha curva. En 1697 Gregory[8], de forma independiente a Hooke, formula la condición de estabilidad del arco cuando menciona la catenaria como directriz óptima. En 1695, La Hire[9] idealiza las dovelas en bolas de billar y observa que la forma resultante es como si engarzaran en un cable perfectamente elástico y sin peso, definiéndose su forma como antifunicular[10], lo contrario del cuelgue natural. Por tanto, el trazado de un arco ideal pasaría por conocer el estado de carga al que está sometido, donde el peso propio del arco es uno de los componentes principales, lo cual implica un proceso iterativo para establecer la forma definitiva.
Couplet, ofreció en 1730 una solución completa al problema, estableciendo el modo de colapso del arco por formación de un mecanismo de cuatro barras; pero fue Coulomb[11] en 1773 quien retomó el problema prácticamente de nuevo, dando una solución sintética a todos los modos de colapso posibles. A finales de la década de 1830, Moseley y Méry desarrollan casi simultáneamente el concepto de línea de empujes, que debe situarse dentro del espesor del arco. En 1833 Navier[12] enuncia la regla del tercio central, por donde debía circular la línea de presiones para evitar las tracciones. Poncelet[13], en 1835, desarrolla un método gráfico que ahorra considerablemente los tiempos de cálculo. Rankine[14] fue el primero en dar una aplicación práctica a la línea de empujes, siendo Barlow y Fuller los encargados de desarrollar la parte gráfica. En 1879 Castigliano[15]abre un nuevo enfoque analítico con planteamientos energéticos, sistematizándose a partir de ese momento el análisis de los arcos de fábrica. Ese mismo año Winkler propuso de forma explícita la aplicación de la teoría elástica para determinar la posición de la línea de empujes.
[1] Leon Battista Alberti (1404-1472), fue arquitecto, matemático, humanista y poeta italiano.
[2] El texto fue descubierto en 1414 por Bracciolini. La edición princeps de la obra vitruviana fue publicada en latín por Giovani Suplicio da Verole en 1486, y en su epístola al cardenal Rafael Riario, se llama a esta obra divinum opus Vitruvi (Blánquez, 2007:XVII). En italiano no se imprimió hasta 1521 y en castellano hasta 1582.
[3] Andrea di Pietro della Góndola, más conocido como Andrea Palladio (1508-1580) fue un reconocido arquitecto italiano del Manierismo, que influyó notablemente en el Neoclasicismo. Una importante aportación a la ingeniería estructural fue la introducción del concepto de cercha o entramado.
[4] Leonardo di ser Piero da Vinci (1452-1519), nacido en Florencia, fue pintor y polímata, genial arquetipo del humanismo renacentista.
[5] Simón Stevenin (1548-1620), fue matemático holandés, ingeniero militar e hidráulico, entre otros oficios.
[6] Pierre Varignon (1654-1722), matemático francés precursor del cálculo infinitesimal, desarrolló la estática de estructuras.
[7] Robert Hooke, científico inglés (1635-1703). Formuló su famosa ley en la que describe cómo un cuerpo elástico se estira de forma proporcional a la fuerza que se ejerce sobre él. En esta época, para reclamar la paternidad de un descubrimiento, los hombres de ciencia enviaban anagramas a sus colegas para, después, cuando las circunstancias eran propicias, les hacían llegar o publicaban el mensaje que los anagramas escondías. Eso fue lo que ocurrió con la descripción que hizo Hooke en 1676 sobre el funcionamiento estructural del arco.
[8] David Gregory (1661-1708), profesor escocés de matemáticas y astronomía en la Universidad de Edimburgo.
[9] Philippe de La Hire, matemático, astrónomo y gnomonicista francés (1640-1719). La obra donde trata el arco es: Traité de mécanique: ou l’on explique tout ce qui est nécessaire dans la pratique des arts, & les propriétés des corps pesants lesquelles ont un plus grand usage dans la physique (1695).
[10] Del latín, funicŭlus, cuerda. Arenas (1996:10) define la antifunicularidad como una afinidad geométrica entre las ordenadas de la directriz de la bóveda y la ley de momentos flectores que produce el sistema de cargas sobre una viga virtual de la misma luz que el arco.
[11] Charles Agustin de Coulomb, físico e ingeniero militar francés (1736-1806), conocido por su famosa ley sobre atracción de cargas eléctricas. Elaboró en el campo estructural la actual teoría de la flexión y una primera teoría de la torsión (1787). También fueron importantes sus ideas sobre la deformación tangencial y el rozamiento.
[12] Claude Louis Marie Henri Navier, ingeniero y físico francés (1785-1836), trabajó en las matemáticas aplicadas a la ingeniería, la elasticidad y la mecánica de fluidos.
[13] Jean Victor Poncelet (1788-1867) fue un matemático e ingeniero francés que recuperó la geometría proyectiva.
[14] William John Macquorn Rankine, ingeniero y físico escocés (1820-1872), conocido también por sus trabajos en termodinámica.
[15] Carlo Alberto Castigliano, ingeniero italiano (1847-1884), elaboró nuevos métodos de análisis para sistemas elásticos.
REFERENCIAS
HEYMAN, J. (1966). The stone skeleton. International Journal of Solids and Structures, 2: 249-279.
HEYMAN, J. (1967). On the shell solutions of masonry domes. International Journal of Solids and Structures, 3: 227-241.
HEYMAN, J. (1999). Teoría, historia y restauración de estructuras de fábrica. CEHOPU, 2ª edición, Madrid.
HUERTA, S. (1996). La teoría del arco de fábrica: desarrollo histórico. Obra Pública, 38:18-29.
HUERTA, S. (2000): Estética y geometría: el proyecto de puentes de fábrica en los siglos XV al XVII, en Graciani, A.; Huerta, S.; Rabasa, E.; Tabales, M. (eds.): Actas del Tercer Congreso Nacional de Historia de la Construcción. Instituto Juan de Herrera/CEHOPU, Sevilla, 513-526.
HUERTA, S. (2005). Mecánica de las bóvedas de fábrica: el enfoque del equilibrio. Informes de la Construcción, 56(496):73-89.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.