Las gráficas de superficie resultan de interés, por ejemplo, para representar la Superficie de Respuesta en un Diseño de Experimentos, o bien cuando estamos representando la predicción de un fenómeno a través de unas redes neuronales. Sea cual sea el motivo, dejo a continuación algunas pautas para que esta tarea sea sencilla.
Sea, por ejemplo, la parametrización de un algoritmo de Simulated Annealing donde hemos realizado experimentos con distintas longitudes de cadenas de Markov (columnas) y distintos coeficientes de enfriamiento (filas). En la tabla se encuentran los resultados medios en coste encontrados tras realizar 9 ensayos en cada caso.
| 20000 | 30000 | 40000 | 50000 | |
| 0,95 | 2652 | 2645 | 2637 | 2634 |
| 0,96 | 2650 | 2644 | 2637 | 2635 |
| 0,97 | 2648 | 2644 | 2637 | 2636 |
| 0,98 | 2647 | 2642 | 2637 | 2636 |
| 0,99 | 2647 | 2641 | 2637 | 2637 |
Para poder representar dichos puntos, necesitamos definir dos vectores fila: x será, por ejemplo, el vector fila de los coeficientes de enfriamiento, e y será el vector fila de las longitudes de cadena de Markov.
>> x=[0.95 0.96 0.97 0.98 0.99]
x =
0.9500 0.9600 0.9700 0.9800 0.9900
>> y=[20000 30000 40000 50000]
y =
20000 30000 40000 50000
>> z=[2652 2645 2637 2634
2650 2644 2637 2635
2648 2644 2637 2636
2647 2642 2637 2636
2647 2641 2637 2637]
z =
2652 2645 2637 2634
2650 2644 2637 2635
2648 2644 2637 2636
2647 2642 2637 2636
2647 2641 2637 2637
Sin embargo, la matriz z tiene que trasponerse, de forma que en filas vengan los datos de y:
>> z=z’
z =
2652 2650 2648 2647 2647
2645 2644 2644 2642 2641
2637 2637 2637 2637 2637
2634 2635 2636 2636 2637
Ahora ya podemos dibujar la superficie, con varias opciones:
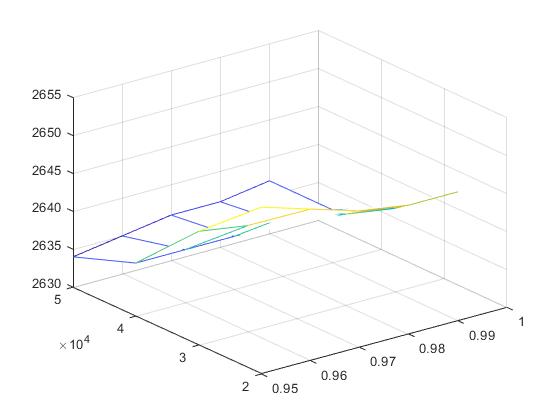
>> mesh (x,y,z)
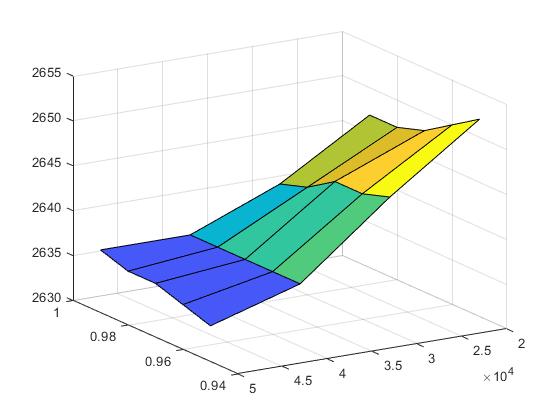
>> surf(x,y,z)
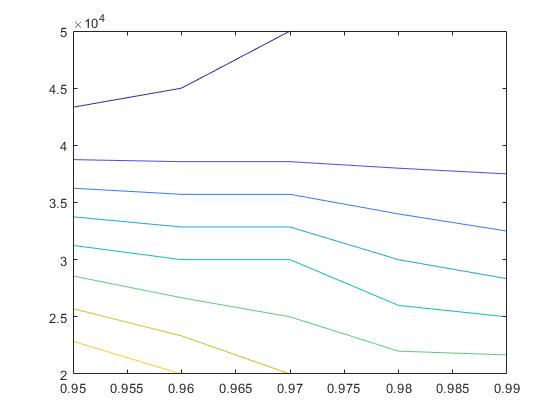
>> contour (x,y,z)
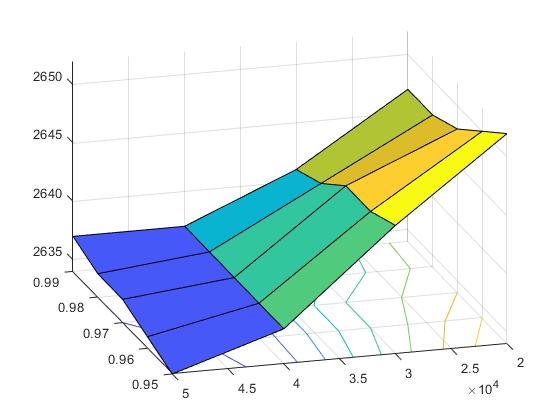
>> surfc (x,y,z)
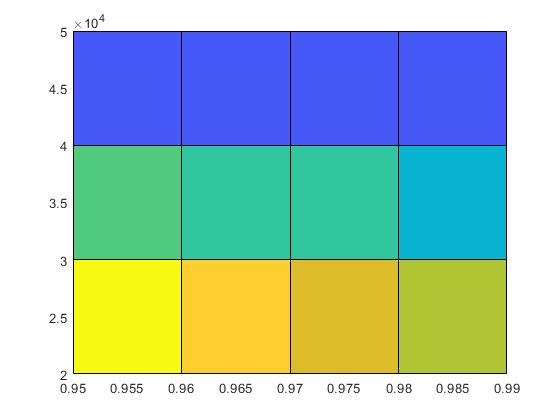
>> pcolor (x,y,z)