Creo interesante comentar en este post los resultados que estamos obteniendo de un Proyecto de Investigación financiado por el Ministerio de Ciencia e Innovación que nuestro grupo de investigación llama HORSOST. Su nombre completo describe el contenido del trabajo que estamos desarrollando: “Diseño eficiente de estructuras con hormigones no convencionales basados en criterios sostenibles multiobjetivo mediante el empleo de técnicas de minería de datos“.
Se trata de un proyecto que empezamos en el año 2012 y que tiene prevista su finalización a finales del 2014. Nuestro grupo de investigación está formado por seis profesores y varios becarios de investigación del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) de la Universidad Politécnica de Valencia. En dicho grupo me corresponde el papel de investigador principal. Espero que esta breve descripción os oriente sobre lo que estamos haciendo.
Este proyecto de investigación se encuentra relacionado con otros ya finalizados y otros en marcha, tanto de convocatorias competitivas como de convenios de transferencia tecnológica con empresas (constructoras, empresas de prefabricados, consultoras, etc.).
El objetivo fundamental del proyecto de investigación HORSOST consiste en establecer pautas de diseño eficiente de estructuras realizadas con hormigón no convencional optimizadas heurísticamente con funciones multiobjetivo relacionadas con la sostenibilidad. Se pretende avanzar en el establecimiento de nuevos diseños que permitan extraer las ventajas que aportan los hormigones especiales, en particular hormigones de alta resistencia, hormigones con fibras, hormigones autocompactantes. Para ello se utiliza el análisis del ciclo de vida de dichas estructuras (elaboración, transporte, procedimientos constructivos, mantenimiento, etc.) considerando aspectos energéticos, medioambientales, sociales y económicos. La optimización heurística permite evaluar los diseños más eficientes, comparar soluciones y generar bases de datos sobre las que aplicar herramientas procedentes de la minería de datos y del aprendizaje automático para extraer información no trivial que permita fórmulas de predimensionamiento. La posibilidad de análisis se debe a que las herramientas matemáticas empleadas presentan un carácter general. Se aplican técnicas como redes neuronales o la teoría del valor extremo además de otras herramientas más habituales como la regresión lineal múltiple o el análisis por componentes principales.
INTRODUCCIÓN
Las evidencias del actual cambio climático, entre otras, han provocado una creciente preocupación por la sostenibilidad [1]. Ello ha impulsado la investigación en aspectos relacionados con la sostenibilidad en el ámbito de la construcción. Así, se han desarrollado indicadores [2] y se han elaborado bases de datos que miden el impacto ambiental de los materiales [3,4], que han servido en algunas investigaciones para reducir las emisiones de CO2 en estructuras [5,6]. Sin embargo, la sostenibilidad requiere contemplar aspectos energéticos, medioambientales, sociales y económicos que deben afectar a todo el ciclo de vida de la estructura [7]. Un antecedente fue el Modelo Integrado de Cuantificación de Valor de un Proyecto Constructivo Sostenible: Aplicación a la Edificación Industrial y de Servicios (MIVES) y MIVES II, la sostenibilidad a través del análisis de valor aplicado a diversos ámbitos [8], que fueron el punto de partida para el Anejo 13 de la actual EHE.
La disponibilidad de ordenadores de elevada potencia de cálculo, junto con el desarrollo de técnicas de análisis inteligente, ha permitido el crecimiento en el diseño de estructuras óptimas [9-11]. Se ha insistido en la necesidad de optimizar estructuras reales, constatándose la escasez de la optimización del hormigón estructural frente a las estructuras metálicas. La optimización [12] puede realizarse desde numerosos puntos de vista (geométrico, topológico, seccional, etc.). Además de los métodos basados en la programación matemática [13], el problema de la optimización se puede abordar mediante técnicas metaheurísticas y bioinspiradas tales como los algoritmos genéticos, el recocido simulado, las colonias de hormigas o las redes neuronales, entre otras [14,15]. Recientemente, el trabajo desarrollado por nuestro grupo ha minimizado el coste de estructuras reales [16-28].
Sin embargo, la optimización ha requerido un intenso trabajo de investigación para extraer conclusiones aplicables a la realidad de las obras. Una forma que tiene el ingeniero para avanzar en el diseño de estructuras que se acerquen a las óptimas es que se difundan fórmulas de predimensionamiento [26,28]. Pues bien, para mejorar los diseños de las estructura, es posible extraer información no trivial de bases de datos de estructuras óptimas empleando la inteligencia artificial.
El descubrimiento de conocimiento en bases de datos (“Knowledge Discovery from Databases”, KDD) constituye un área donde se están realizando muchos esfuerzos, tanto en metodología como en investigación. En este contexto, la minería de datos constituye un conjunto de herramientas empleadas para la extracción de información no trivial que reside de manera implícita en los datos [29]. Mediante este tipo de técnicas se pueden solucionar problemas de predicción, clasificación y segmentación [30]. Algunas de sus herramientas más representativas son las redes neuronales, las máquinas de soporte vectorial, los árboles de decisión, modelos estadísticos avanzados multivariantes y de diseños de experimentos y el agrupamiento o “clustering”. Estas herramientas construyen modelos abstractos a partir de datos basándose en métodos de aprendizaje automático “machine learning”.
Por otra parte, la investigación en hormigones no convencionales constituye una de las líneas de investigación relevantes relacionada con los nuevos materiales de construcción. Sus propiedades permiten mejorar las prestaciones y la durabilidad, y ello se encuentra relacionado con la sostenibilidad de su uso. Así, el refuerzo con fibras (HRF) reduce la fisuración y mejora la durabilidad al impedir el acceso de agua y contaminantes [31]. Sin embargo, razones económicas han llevado al empleo de fibras sólo en casos puntuales, cuando existen beneficios adicionales relativos a mano de obra, durabilidad o congestión del refuerzo [32]. El hormigón autocompactante (HAC) ha mejorado significativamente la tecnología del hormigón, al conseguir estructuras más durables, mejorar la producción y los procesos constructivos, facilitar el diseño de elementos complejos y acabados. Ello se consigue con dosificaciones que cambian las propiedades mecánicas respecto al hormigón convencional [33]. Todo ello abre horizontes inexplorados, donde una simple optimización económica de las estructuras haría inviable el empleo de muchos hormigones especiales, pero donde una visión más amplia que contemple criterios de sostenibilidad y de análisis del ciclo de vida, puede cambiar la perspectiva en cuanto a su empleo.
Hipótesis de partida y objetivos del proyecto
El objetivo fundamental de HORSOST consiste en establecer criterios de diseño eficiente basados en el análisis del ciclo de la vida de estructuras de hormigón no convencional, aplicando para ello técnicas procedentes de la inteligencia artificial y la minería de datos a amplios conjuntos de estructuras optimizadas heurísticamente bajo objetivos múltiples de sostenibilidad (ahorro energético y de recursos naturales, aspectos ambientales, sociales y económicos).
Hipótesis de partida
a) Es posible mejorar los diseños de las estructuras de hormigón a través de pautas de predimensionamiento sólo disponibles por algunos proyectistas de gran experiencia.
b) Existen criterios de diseño que permiten compatibilizar las exigencias derivadas de la sostenibilidad con reducciones de coste, con aumentos en seguridad y constructibilidad. Sin embargo, estos criterios no son triviales.
c) Los hormigones no convencionales presentan propiedades que permiten contribuir a la sostenibilidad de las estructuras cuando se analiza el ciclo de vida.
d) La inteligencia artificial y la minería de datos permiten aflorar relaciones no triviales cuando existen bases de datos suficientemente amplias.
e) La optimización heurística permite elaborar bases masivas de datos de estructuras optimizadas bajo objetivos múltiples basados en la sostenibilidad (huella ecológica, reducción de CO2, etc.).
Objetivos del proyecto
1. Desarrollar una metodología capaz de extraer información no trivial de bases de datos masivas de estructuras de hormigón no convencional optimizadas con múltiples objetivos basados en la sostenibilidad.
2. Obtener reglas de predimensionamiento optimizadas para cada una de las tipologías estructurales. La novedad y relevancia consiste en utilizar herramientas procedentes del “data mining” y de “machine learning”.
3. Comparar las reglas de diseño obtenidas para hormigones convencionales y no convencionales, así como con criterios obtenidos de la práctica habitual de diseño y de la bibliografía existente.
4. Divulgar el conocimiento adquirido para que los proyectistas puedan utilizar estos criterios de predimensionamiento, de forma que se puedan conseguir mejoras respecto a la sostenibilidad a lo largo del ciclo de vida de las estructuras de hormigón no convencional.
Descripción de la metodología empleada en el proyecto
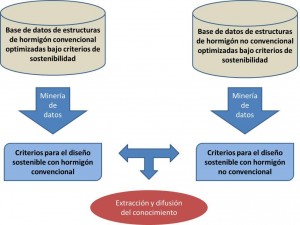
La metodología empleada consta de una secuencia iterativa de fases (Figura 1):
- Integración y recopilación de datos, donde se determinan las fuentes de información que pueden ser útiles y dónde conseguirlas.
- Selección, limpieza y transformación de datos, donde se eliminan o corrigen los datos incorrectos y se decide la estrategia a seguir con los datos incompletos.
- Minería de datos, donde se decide la tarea a realizar, ya sea la clasificación, la regresión, el agrupamiento o las reglas de asociación.
- Evaluación e interpretación, donde se evalúan los patrones y se analizan por el equipo investigador, volviéndose a fases anteriores para nuevas iteraciones si fuera necesario.
- Difusión, donde se hace uso del nuevo conocimiento adquirido y se hace partícipe de él a todos los posibles usuarios.
Figura 1 Extracción y difusión del conocimiento por contraste de criterios de diseño sostenible
Uno de los aspectos clave es la disposición de datos utilizables, en cantidad y calidad suficientes, para aplicar las técnicas de “data mining”. Se trata de aplicar un procedimiento convergente para la generación de bases de datos (CGD, para abreviar). A continuación se describe el fundamento y la forma de proceder de CGD.
Una estructura de hormigón se puede representar mediante una serie de variables y parámetros. Pues bien, la complejidad de un problema aumenta drásticamente con el número variables involucradas [34], efecto denominado como la “maldición de la dimensión” [35]. Para poder extraer información, como regla práctica [36] se necesita una muestra cuyo número sea, al menos, de 10 veces el número de variables independientes, siendo deseable que ese ratio fuera mayor a 20. En el caso de un puente pretensado [37], el número de factores que son combinación lineal de las variables originales y que, además sean independientes entre sí es de 4, por lo que se precisaría en torno a 40-80 casos para poder realizar inferencias lineales, lo cual no contemplaría relaciones cruzadas entre variables (ello implicaría muestra mayor). Otras técnicas como las redes neuronales o las máquinas de soporte vectorial, que son capaces de inferir modelos no lineales e incluso discontinuos o discretos, requieren un número mayor de individuos. Además, se aconseja la reserva un grupo de validación, que puede oscilar entre 1/3 y 1/4 de la muestra necesaria, para comprobar que las inferencias presentan una calidad adecuada.
Metaheurísticas empleadas en el desarrollo del proyecto
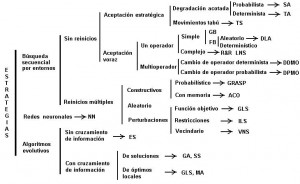
Desde los primeros años de la década de los 80, la investigación de los problemas de optimización se centra en el diseño de métodos aproximados basados en conceptos derivados de la inteligencia artificial, la evolución biológica y la mecánica estadística. En la Figura 2 se recoge una clasificación propuesta por Yepes [39] que debería complementarse con metaheurísticas híbridas que emplean, en mayor o menor medida, estrategias de unos grupos y otros. A continuación se describen algunas técnicas empleadas en HORSOST.
Figura 2 Taxonomía de estrategias empleadas en la resolución aproximada de problemas de optimización combinatoria [39]
Recocido simulado
El recocido simulado “Simulated Annealing” (SA) [40,41] se basa en la analogía de la energía de un sistema termodinámico con la función de coste de un problema de optimización. Conceptualmente es un algoritmo de búsqueda por entornos, donde una solución sustituye a la anterior si mejora a la anterior (D£0); en caso contrario, será aceptada con una probabilidad (e(-D/T) si D>0, donde T es un parámetro denominado temperatura) decreciente con el aumento D de la diferencia entre los costes de la solución candidata y la actual. La selección aleatoria de soluciones degradadas permite eludir los óptimos locales.
Aceptación por umbrales
La aceptación por umbrales “Threshold Accepting” (TA) [42] emplea un enfoque parecido a SA para eludir los óptimos locales, pero donde la toma de decisiones es más sencilla. Se autoriza el menoscabo en la calidad de las soluciones siempre y cuando no se exceda en cierta magnitud la aptitud de la solución actual.
Sistema de colonia de hormigas
El sistema de colonia de hormigas “Ant System Optimization” (ACO) [43] se basa en la analogía del comportamiento de estos insectos cuando encuentran el camino más corto entre la comida y su hormiguero. Tan pronto como un individuo encuentra una fuente de comida, evalúa su cantidad y calidad y transporta un poco al hormiguero. Durante el regreso, la hormiga deja por el camino feromonas, para que las demás puedan seguirla. Después de un tiempo, el camino hacia el alimento se indicará por un rastro oloroso que crece con el número de hormigas que pasen por él, y que va desapareciendo en caso contrario. El resultado final es la optimización del trabajo de todo el hormiguero en su búsqueda de comida.
Búsqueda local iterada
La idea de la búsqueda local iterada “Iterated Local Search” (ILS) [44] consiste en rastrear la solución entre el subespacio definido por los óptimos locales. Dado que un algoritmo de búsqueda es capaz de transformar una solución s en otra s* que es un óptimo local, para pasar a otro óptimo local cercano s’, se provoca una pequeña perturbación. Aplicando el algoritmo de búsqueda a s’ se encuentra otra solución s*’. La metaheurística acepta el paso de s* a s*’ mediante algún criterio como el de máximo gradiente (si s*’ es mejor que s*, se acepta) o no (se puede pensar en un mecanismo TA o SA para evitar estancamientos dentro del subespacio de los óptimos locales s*).
Búsqueda en entornos variables
La búsqueda en entornos variables “Variable Neighborhood Search” (VNS) [45] consiste en cambiar de operador de búsqueda cuando el anterior ha llegado a un óptimo local. De este modo, VNS oscilará entre dos o más operadores con la esperanza que los cambios en la estructura del entorno permitirán escapar de muchos óptimos locales. Para que este principio trabaje bien, los operadores empleados deberán ser lo suficientemente distintos en relación con la estructura del vecindario que generan.
Algoritmos genéticos
Los algoritmos genéticos “Genetic Algorithms” (GA) [46] simulan el proceso de evolución de las especies que se reproducen sexualmente. Un nuevo individuo se genera a través del cruzamiento, que combina parte del patrimonio genético de cada progenitor para elaborar el del nuevo individuo, y de la mutación, que supone una modificación espontánea de esta información genética. Si los hijos heredan buenos atributos de sus padres, su probabilidad de supervivencia será mayor, reproduciéndose con mayor probabilidad.
Algoritmos meméticos
Los algoritmos meméticos “Memetic Algorithms” (MA) [47] derivan de GA, donde el empleo de una población de soluciones se compagina con heurísticas de búsqueda local. La idea consiste en recombinar la información de las soluciones provenientes del subespacio de óptimos locales. El éxito de estos métodos puede ser atribuido a su balance entre la búsqueda rápida, y el mantenimiento de la diversidad para evitar la convergencia prematura.
Otras técnicas empleadas en el proyecto
Regresión lineal múltiple
Los modelos de regresión lineal múltiple (RLM) se ajustan por mínimos cuadrados de forma que la variable de respuesta se encuentre explicada al máximo posible por las variables independientes. El proceso se inicia intentando explicar la respuesta en función de aquella variable con la que presenta una mayor correlación. El objetivo es aumentar el coeficiente de regresión agregando variables independientes explicativas, usando para ello el método stepwise de pasos sucesivos [48].
Análisis por componentes principales
El análisis de componentes principales (ACP) examina la interdependencia entre variables para reducir su dimensión a un nuevo subconjunto formado por variables no observables. En síntesis, calcula unos factores que sean combinación lineal de las variables originales y que, además, sean independientes entre sí. La primera componente principal se escoge de forma que explique la mayor parte de la varianza posible, y así sucesivamente. Para facilitar la interpretación, se emplea una rotación ortogonal que minimiza el número de variables que tienen saturaciones altas en cada factor [49].
Redes neuronales artificiales
Las redes neuronales artificiales “Artificial Neural Networks” (ANN) simulan un sistema de procesamiento de la información altamente complejo, no lineal y en paralelo parecido al cerebro humano. McCulloch y Pitts [50] presentaron el primer modelo de neurona como un dispositivo no lineal multientrada con interconexiones “con peso”. La neurona suma las entradas ya ponderadas, les aplica una función no lineal y transmite una salida. La red puede ser preparada, utilizando ejemplos, para reconocer ciertas estructuras, como puede ser la clasificación de objetos por sus características o la inferencia a partir de los datos de entrada.
Teoría del valor extremo
Si se acepta que el óptimo local encontrado por un algoritmo de búsqueda estocástico puede considerarse como una solución extrema de una muestra aleatoria simple constituida por las soluciones visitadas, entonces se podría aplicar la teoría del valor extremo “Extreme Value Theory” (EVT) [51,52] para estimar el óptimo global del problema. Para ello se ha comprobado que los óptimos locales encontrados constituyen valores extremos que ajustan a una función Weibull de tres parámetros, siendo el de posición, γ, una estimación del óptimo global.
Tabla 1 Referencias del empleo de técnicas respecto a tipologías estructurales
|
|
SA |
TA |
ACO |
ILS |
VNS |
GA |
MA |
EVT |
ANN |
ACP |
RLM |
|
Muros |
[28] |
[6] |
|
|
[6] |
|
|
|
|
|
|
|
Pórticos de edificación |
[5,24] |
|
|
|
|
|
|
[24] |
|
|
|
|
Vigas de hormigón armado |
|
[27] |
|
|
[27] |
|
|
[27] |
|
|
|
|
Vigas pretensadas |
|
|
|
|
|
|
|
|
[23] |
|
|
|
Bóvedas de paso inferior |
[16] |
[16] |
|
[17] |
|
|
|
[17] |
|
|
|
|
Marcos de paso inferior |
[25] |
[25,26] |
|
|
|
|
|
|
|
|
|
|
Pilas de puente |
[21] |
|
[20,22] |
|
|
[20] |
|
|
|
|
|
|
Puentes de vigas artesa |
[18] |
|
|
|
|
|
[19] |
|
|
|
|
|
Puentes losa postesados |
|
|
|
|
|
|
|
|
|
[37] |
[37] |
Conclusiones
Como conclusiones generales del planteamiento del proyecto HORSOST se pueden citar las siguientes:
1) Existe una importante área de mejora en los diseños de estructuras de hormigón no convencional de forma que se obtenga un importante beneficio social si estos diseños maximizan la sostenibilidad en la construcción de estas estructuras considerando todo el ciclo de vida del producto.
2) Es posible emplear técnicas procedentes del descubrimiento de conocimiento en bases de datos (KDD) para extraer información no trivial de bases de datos de estructuras de hormigón generadas a partir de la optimización heurística multiobjetivo basada en la sostenibilidad.
3) Los hormigones no convencionales presentan prestaciones que favorecen su durabilidad y, por ello, pueden contribuir a la sostenibilidad si se consideran aspectos medioambientales, sociales y económicos a lo largo de toda su vida útil. Por tanto, se deben analizar en detalle para comprobar su validez frente a los hormigones convencionales y ofrecer criterios de diseño aplicables por los proyectistas.
Agradecimientos
Los autores agradecen el aporte financiero realizado para este trabajo por el Ministerio de Ciencia e Innovación (Proyecto de Investigación BIA2011-23602) y por la Universitat Politècnica de València (Proyecto de Investigación PAID-06-12).
Referencias
[1] Baldasano, J.M. (2007). Evidencias del actual cambio climático, en Cambio climático y sus consecuencias. Generalitat Valenciana, pp. 43-56.
[2] Rodríguez, F.; Fernández, G. (2010). Ingeniería sostenible: nuevos objetivos en los proyectos de construcción. Revista Ingeniería de Construcción, 25(2), 147-160. [doi:10.4067/S0718-50732010000200001]
[3] Goedkoop, M.; Spriensma, R. (2001). The Ecoindicator 99: A damage oriented method for life cycle impact assessment. Methodology Report. Product Ecology Consultants, Amersfoort, Netherlands.
[4] Institut de Tecnologia de la Construcció de Catalunya (2009). BEDEC PR/PCT ITEC materials database. Available online at:http://www.itec.es/nouBedec.e/presentaciobedec.aspx
[5] Payá-Zaforteza I.; Yepes, V.; Hospitaler, A.; González-Vidosa, F. (2009). CO2-Efficient Design of Reinforced Concrete Building Frames. Engineering Structures, 31, 1501-1508. [doi.org/10.1016/j.engstruct.2009.02.034]
[6] Yepes, V.; González-Vidosa, F.; Alcalá, J.; Villalba, P. (2012). CO2-Optimization Design of Reinforced Concrete Retaining Walls based on a VNS-Threshold Acceptance Strategy. Journal of Computing in Civil Engineering ASCE, 26 (3), 378-386. [doi:10.1061/(ASCE)CP.1943-5487.0000140]
[7] Burón, M. (2007). La sostenibilidad de las construcciones de hormigón. Revista Técnica Cemento Hormigón, 897, 58-65.
[8] Aguado, A.; Alarcón, D.B.; Manga, R. (2008). Razón de ser del anejo ICES de la EHA y características del mismo. Revista Técnica Cemento Hormigón, 913, 16-23.
[9] Sriram, R.D. (2006). Artificial intelligence in engineering: personal reflections. Advanced Engineering Informatics, 20, 3-5. [doi:10.1016/j.aei.2005.12.002]
[10] Sarma, K.C.; Adeli, H. (1998). Cost optimization of concrete structures. ASCE Journal of Structural Engineering, 124(5), 570-578. [doi:10.1061/(ASCE)0733-9445(1998)124:5(570)]
[11] Cohn, M.Z.; Dinovitzer, A.S. (1994). Application of structural optimization. ASCE Journal of Structural Engineering, 120(2), 617-649. [doi:10.1061/(ASCE)0733-9445(1994)120:2(617)]
[12] Martínez, P.; Martí, P.; Querín, O.M. (2007). Growth method for size, topology, and geometry optimization of truss structures. Structural and Multidisciplinary Optimization, 33, 13-26. [doi:10.1007/s00158-006-0043-9]
[13] Hernández, S.; Fontan, A. (2002). Practical Applications of Design Optimization. WIT Press, Southampton.
[14] Adeli, H.; Sarma, K.C. (2006). “Cost optimization of structures. Fuzzy logic, genetic algorithms and parallel computing”, Wiley, Chichester.
[15] Dreo, J.; Petrowsky, A.; Siarry, P.; Taillard, E. (2006). Metaheuristics for hard optimization. Methods and case studies. Springer, Berlin Heidelberg.
[16] Carbonell, A.; González-Vidosa, F.; Yepes, V. (2011). Heuristic optimization of reinforced concrete road vault underpasses. Advances in Engineering Software, 42(4), 151-159. [doi:10.1016/j.advengsoft.2011.01.002]
[17] Carbonell, A.; Yepes, V.; González-Vidosa, F. (2012). Automatic design of concrete vaults using iterated local search and extreme value estimation. Latin American Journal of Solids and Structures, 9(6), 675-689.
[18] Martí, J.V.; González-Vidosa, F.; Yepes, V.; Alcalá, J. (2013). Design of prestressed concrete precast road bridges with hybrid simulated annealing. Engineering Structures, 48, 342-352. [doi:10.1016/j.engstruct.2012.09.014]
[19] Martí, J.V.; Yepes, V.; González-Vidosa, F.; Luz, A. (2013). Diseño automático de tableros óptimos de puentes de carretera de vigas artesa prefabricadas mediante algoritmos meméticos híbridos. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, (en prensa).
[20] Martínez-Martín, F.; González-Vidosa, F.; Hospitaler, A.; Yepes, V. (2010). Heuristic Optimization of RC Bridge Piers with Rectangular Hollow Sections. Computers & Structures, 88(5-6), 375-386. [doi:10.1016/j.compstruc.2009.11.009]
[21] Martínez-Martín, F.; González-Vidosa, F.; Hospitaler, A.; Yepes, V. (2012). Multi-objective optimization design of bridge piers with hybrid heuristic algorithms. Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering, 13(6), 420-432. [doi:10.1631/jzus.A1100304]
[22] Martínez-Martín, F.; González-Vidosa, F.; Hospitaler, A.; Yepes, V. (2013). A parametric study of optimum tall piers for railway bridge viaducts. Structural Engineering and Mechanics, 45(6), 723-740.
[23] Martí-Vargas, J.R.; Ferri, F.J.; Yepes, V. (2013). Prediction of the transfer length of prestressing strands with neural networks. Computers and Concrete, (in press).
[24] Payá-Zaforteza, I.; Yepes, V.; González-Vidosa, F.; Hospitaler, A. (2010). On the Weibull cost estimation of building frames designed by simulated annealing. Meccanica, 45(5), 693-704. [doi:10.1007/s11012-010-9285-0]
[25] Perea, C.; Alcalá, J.; Yepes, V.; González-Vidosa, F.; Hospitaler, A. (2008). Design of Reinforced Concrete Bridge Frames by Heuristic Optimization. Advances in Engineering Software, 39(8), 676-688. [doi:10.1016/j.advengsoft.2007.07.007]
[26] Perea, C.; Yepes, V.; Alcalá, J.; Hospitaler, A.; González-Vidosa, F. (2010). A parametric study of optimum road frame bridges by threshold acceptance. Indian Journal of Engineering & Materials Sciences, 17(6), 427-437.
[27] Torres-Machí, C.; Yepes, V.; Alcalá, J.; Pellicer, E. (2013). Optimization of high-performance concrete structures by variable neighborhood search. International Journal of Civil Engineering, Transaction A: Civil Engineering, 11(2), 90-99.
[28] Yepes, V.; Alcalá, J.; Perea, C.; González-Vidosa, F. (2008). A Parametric Study of Optimum Earth Retaining Walls by Simulated Annealing. Engineering Structures, 30(3), 821-830. [doi:10.1016/j.engstruct.2007.05.023]
[29] Fayyad, U.M. (1996). Data Mining and Knowlegde Discovery: Making Sense Out of Data. IEEE Expert, 11(5), 20-25. [doi:10.1109/64.539013]
[30] Hernández, J.; Ramírez, M.J.; Ferri, C. (2004). Introducción a la minería de datos. Pearson, Madrid.
[31] Rossi, P.; Chanvillard, G. (eds.) (2000). “Fibre-Reinforced Concretes (FRC)”. Proceedings of the 5th International RILEM Symposium (BEFIB 2000). RILEM Publications S.A.R.L., Cachan, France.
[32] Massicitte, B. (2000). Fiber Reinforce Concrete: a Structural Perspective, RILEM Proceedings 15, BEFIB 2000.
[33] Martí-Vargas, J.R.; Serna-Ros, P.; Arbeláez, C.A.; Rigueira-Víctor, J.W. (2006). Comportamiento adherente del hormigón autocompactante en transmisión y anclaje. Materiales de Construcción, 56(284), 27-42.
[34] Pettis, K.W.; Bailey, T.A.; Jain, A.K.; Dubes, R.C. (1979). An intrinsic dimensionality estimator from near-neighbor information. IEEE Transactions on pattern analysis and machine intelligence, 1, 25-37. [doi:10.1109/TPAMI.1979.4766873]
[35] Bellman, R.E. (1961). Adaptive Control Processes. Princeton University Press, Princeton, N.J.
[36] Fukunaga, M. (1990). Introduction to Statistical Pattern Recognition. 2nd Edition. Academic Press, San Diego, USA.
[37] Yepes, V.; Díaz, J.; González-Vidosa, F.; Alcalá, J. (2009). Caracterización estadística de tableros pretensados para carreteras. Revista de la Construcción, 8(2), 95-109.
[38] Ferri, J.; Diaz-Chito, K.; Diaz-Villanueva, W. (2010). Efficient dimensionality reduction on undersampled problems through incremental discriminative common vectors, ICDM’10 (OEDM Workshop), pp. 1159-1166.
[39] Yepes, V. (2002). Optimización heurística económica de redes de transporte del tipo VRPTW. Tesis doctoral, Universitat Politècnica de València.
[40] Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. (1983). Optimization by simulated annealing. Science, 220(4598), 671-680. [doi:10.1126/science.220.4598.671]
[41] Cerny, V. (1985). Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. Optimization Theory and Applications, 45, 41-51. [doi:10.1007/BF00940812]
[42] Dueck G, Scheuer T. (1990). Threshold accepting: a general purpose optimization algorithm superior to simulated annealing. Journal of Computational Physics, 90(1), 161–75. [doi:10.1016/0021-9991(90)90201-B]
[43] Dorigo, M.; Maniezzo, V.; Colorni, A. (1996). The ant system: optimization by a colony of cooperating agents. IEEE Transactions on Systems, Man, and Cybernetics-Part B, 26(1), 29-41. [doi:10.1109/3477.484436]
[44] Lourenço, H.R.; Martin, O.C.; Stülze, T. (2003). Iterated local search. In F.W. Glover and G.A. Kochenberger, edi-tors, Handbook of metaheuristics, pages 321-353, Boston, Dordrecht, London. Kluwer Academic Publishers.
[45] Mladenovic, N.; Hansen, P. (1997). Variable neighborhood search. Computers and Operations Research, 24(11), 1097-1100. [doi:10.1016/S0305-0548(97)00031-2]
[46] Holland, J.H. (1975). Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor.
[47] Moscato, P. On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Technical Report Caltech Concurrent Computation Program Report 826, Caltech, Pasadena, California, USA.
[48] Hocking, R. (1976). The Analysis and Selection of Variables in Linear Regression. Biometrics, 32, 1-49.
[49] Kaiser H.F. (1958). The Varimax criterion for analytic rotation in factor analysis. Psychometrika, 23(3), 187-200. [doi:10.1007/BF02289233]
[50] McCulloch, W.; Pitts, W. (1943). A logical calculus of ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 5, 115-133. [doi:10.1016/S0092-8240(05)80006-0]
[51] McRoberts, K. (1971). A search model for evaluating combinatorially explosive problems. Operations Research, 19(6), 1331-1349. [doi:10.1287/opre.19.6.1331]
[52] Golden, B.L.; Alt, F.B. (1979). Interval estimation of a global optimum for large combinatorial problems. Naval Research Logistics Quarterly, 26(1), 69-77. [doi: 10.1002/nav.3800260108]