Introducción: La ciencia oculta de las encuestas.
Introducción: La ciencia oculta de las encuestas.
Todos hemos pasado por ello: cuestionarios interminables, preguntas que parecen sacadas de un manual de psicología y, sobre todo, esa sensación de responder a la misma pregunta una y otra vez. Es una experiencia tan común como, a menudo, frustrante. ¿Por qué algunas preguntas parecen extrañas o repetitivas? ¿Realmente merece la pena todo este esfuerzo?
La respuesta es un rotundo sí. Detrás de cada cuestionario bien diseñado se esconde la rigurosa ciencia de la psicometría, el campo dedicado al arte de la medición precisa. Conceptos como la fiabilidad y la validez son los pilares de cualquier instrumento de medición serio, ya sea una encuesta de satisfacción del cliente o un test de personalidad.
Este artículo desvela algunos de los secretos más sorprendentes y fascinantes sobre cómo se construyen estas escalas de medida. Descubrirás por qué la repetición puede ser una virtud, por qué la perfección a veces es sospechosa y por qué es posible equivocarse de manera confiable.
Primer secreto: la fiabilidad no es la validez (y se puede estar fiablemente equivocado).
En el mundo de la medición, la fiabilidad y la validez son dos conceptos cruciales que a menudo se confunden. Sin embargo, comprender su diferencia es fundamental para entender por qué algunas encuestas funcionan y otras no.
- La fiabilidad se refiere a la precisión o consistencia de una medida. Un instrumento fiable produce resultados muy similares cada vez que se utiliza en las mismas condiciones.
- La validez es la exactitud de la medida. Un instrumento válido mide exactamente lo que se pretende medir. La validez va más allá de la simple exactitud, ya que se asegura de que las conclusiones que extraemos de los resultados de la encuesta estén justificadas y sean significativas.
La mejor manera de entenderlo es mediante la analogía de un tirador que apunta a una diana.
- Fiabilidad sin validez: imagina a un tirador. Escuchas el sonido seco y repetitivo de los disparos impactando en la madera, agrupados en un área no mayor que una moneda, pero peligrosamente cerca del borde de la diana. El patrón es muy consistente (alta fiabilidad), pero erróneo de forma sistemática, ya que no alcanza el blanco (baja validez). Esto representa un error sistemático que se debe a un defecto fundamental en el diseño del cuestionario, como preguntas mal redactadas o una escala de respuesta poco clara.
- Validez con baja fiabilidad: ahora imagina a un tirador cuyos disparos están dispersos por toda la diana, pero cuya media se sitúa justo en el centro. No hay precisión en cada tiro (baja fiabilidad), pero, en conjunto, apuntan en la dirección correcta (alta validez). Esto representa errores aleatorios que pueden deberse a factores incontrolables, como distracciones, ruido ambiental o incluso al estado de ánimo temporal del encuestado.
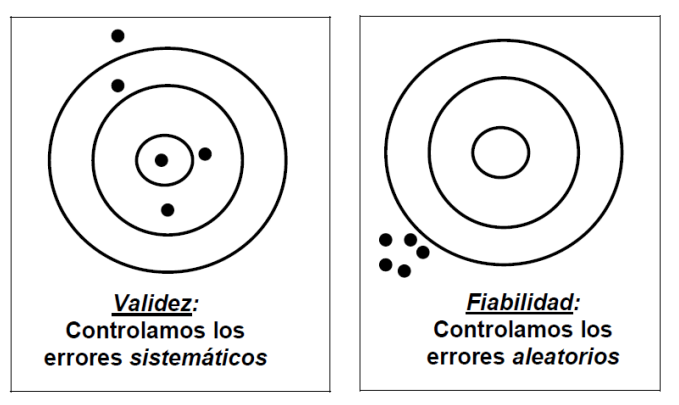
La conclusión clave es que la validez es más importante que la fiabilidad. Como subrayan los expertos en la materia: «Un instrumento puede ser muy fiable (medir muy bien), pero no medir bien lo que se quería medir». De nada sirve medir algo con una precisión milimétrica si no es lo que realmente nos interesa.
Segundo secreto: ¿por qué las encuestas a veces parecen repetitivas?
Una de las quejas más comunes sobre los cuestionarios es que incluyen preguntas que parecen decir lo mismo de distintas maneras. Lejos de ser un descuido, el uso de lo que los expertos denominan «ítems repetitivos» —expresar la misma idea de diversas formas— es una técnica deliberada y muy útil para garantizar la calidad de los datos. Esta «forma bidireccional de redactar los ítems» tiene dos ventajas principales:
- Requiere mayor atención del sujeto: al presentar la misma idea con formulaciones distintas (a veces en positivo y otras en negativo), se evita que la persona responda de forma automática o sin pensar y se le obliga a procesar el significado de cada pregunta.
- Permite comprobar la coherencia de las respuestas: sirve como control de calidad para detectar y mitigar dos de los sesgos más frecuentes al responder encuestas: la aquiescencia y el sesgo de confirmación.
-
- Aquiescencia: tendencia a estar de acuerdo con todas las afirmaciones. Imagina a alguien que responde con prisas, marcando «Totalmente de acuerdo» a todo («Sí, el servicio fue excelente», «Sí, el producto es terrible»), con el único fin de terminar cuanto antes.
- Deseabilidad social: tendencia a responder para proyectar una buena imagen. Este sesgo lo muestra la persona que, al ser preguntada por sus hábitos de reciclaje, se presenta como un ecologista modelo, aunque el contenido de su cubo de basura cuente una historia muy diferente.
Por lo tanto, la próxima vez que te encuentres con preguntas que te resulten familiares en un mismo cuestionario, recuerda que no se trata de un error. Se trata de una herramienta diseñada para garantizar que tus respuestas sean más atentas, coherentes y, en última instancia, sinceras.
Tercer secreto: una fiabilidad «perfecta» puede ser una señal de alarma.
Intuitivamente, podríamos pensar que el objetivo de cualquier escala de medida es lograr la mayor fiabilidad posible. Sin embargo, en psicometría, una fiabilidad extremadamente alta puede ser una señal de alarma que indica un problema subyacente.
El coeficiente de fiabilidad más utilizado, el alfa de Cronbach, presenta una particularidad: su valor tiende a aumentar al añadir más ítems a la escala. Esto crea la tentación de inflar artificialmente la fiabilidad simplemente alargando el cuestionario. Como advierte la literatura especializada: «No se debe buscar una alta fiabilidad aumentando sin más el número de ítems, sin pensar si realmente son válidos».
 Un ejemplo hipotético ilustra perfectamente este peligro. Imaginemos que aplicamos un test a un grupo mixto compuesto por niñas de 10 años que hacen ballet y niños de 14 años que juegan al fútbol. Les preguntamos por su edad, su sexo y el deporte que practican. La fiabilidad estadística se dispara porque las preguntas son perfectamente consistentes al separar a los dos grupos. Si se pregunta sobre ballet, todas las niñas responden de una manera y todos los niños de otra. Si se pregunta por el fútbol, ocurre lo mismo. El algoritmo estadístico detecta esta consistencia impecable y reporta una fiabilidad altísima, sin comprender que el «rasgo» subyacente que se está midiendo es simplemente una mezcla de datos demográficos, no una característica psicológica coherente. A pesar de esa elevada fiabilidad, en realidad no estaríamos midiendo «nada interpretable».
Un ejemplo hipotético ilustra perfectamente este peligro. Imaginemos que aplicamos un test a un grupo mixto compuesto por niñas de 10 años que hacen ballet y niños de 14 años que juegan al fútbol. Les preguntamos por su edad, su sexo y el deporte que practican. La fiabilidad estadística se dispara porque las preguntas son perfectamente consistentes al separar a los dos grupos. Si se pregunta sobre ballet, todas las niñas responden de una manera y todos los niños de otra. Si se pregunta por el fútbol, ocurre lo mismo. El algoritmo estadístico detecta esta consistencia impecable y reporta una fiabilidad altísima, sin comprender que el «rasgo» subyacente que se está midiendo es simplemente una mezcla de datos demográficos, no una característica psicológica coherente. A pesar de esa elevada fiabilidad, en realidad no estaríamos midiendo «nada interpretable».
Este ejemplo nos deja una lección fundamental que el texto fuente resume de manera brillante:
«En ningún caso la estadística sustituye al sentido común y al análisis lógico de nuestras acciones».
Conclusión: la próxima vez que rellenes una encuesta…
Desde el dilema fundamental entre mediciones consistentes, pero erróneas (fiabilidad frente a validez), pasando por el uso deliberado de la repetición para burlar nuestros propios sesgos, hasta la idea contraintuitiva de que una puntuación «perfecta» puede indicar un resultado sin sentido, queda claro que elaborar una buena encuesta es un trabajo científico.
La próxima vez que te enfrentes a un cuestionario, en lugar de frustrarte por sus preguntas, ¿te detendrás a pensar qué rasgo intentan medir y si realmente lo están logrando?
En este audio os dejo una conversación sobre estas ideas.
Os dejo un vídeo que resume el contenido de este artículo.
Referencias:
Campbell, D. T., & Fiske, D. W. (1959). Convergent and discriminant validation by the multitrait–multimethod matrix. Psychological Bulletin, 56(2), 81–105. https://doi.org/10.1037/h0046016
Dunn, T. J., Baguley, T., & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 105, 399–412. https://doi.org/10.1111/bjop.12046
Farrell, A. M. (2010). Insufficient discriminant validity: A comment on Bove, Pervan, Beatty and Shiu (2009). Journal of Business Research, 63, 324–327. https://ssrn.com/abstract=3466257
Fornell, C., & Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of Marketing Research, 18(1), 39–50. https://doi.org/10.1177/002224378101800104
Frías-Navarro, D. (2019). Apuntes de consistencia interna de las puntuaciones de un instrumento de medida. Universidad de Valencia. https://www.uv.es/friasnav/AlfaCronbach.pdf
Grande, I., & Abascal, E. (2009). Fundamentos y técnicas de investigación comercial. Madrid: ESIC.
Hernández, B. (2001). Técnicas estadísticas de investigación social. Madrid: Díaz de Santos.
Hair, J. F., Anderson, R. E., Tatham, R. L., & Black, W. C. (1995). Multivariate data analysis (Eds.). New York: Prentice Hall International, Inc.
Kotler, P., & Armstrong, G. (2001). Marketing. México: Pearson Prentice Hall.
Matas, A. (2018). Diseño del formato de escalas tipo Likert: un estado de la cuestión. Revista Electrónica de Investigación Educativa, 20(1), 38–47. http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1607-40412018000100038
Morales, P. (2006). Medición de actitudes en psicología y educación. Madrid: Universidad Pontificia de Comillas.
Morales, P. (2008). Estadística aplicada a las ciencias sociales. Madrid: Universidad Pontificia Comillas.
Nadler, J., Weston, R., & Voyles, E. (2015). Stuck in the middle: The use and interpretation of mid-points in items on questionnaires. The Journal of General Psychology, 142(2), 71–89. https://doi.org/10.1080/00221309.2014.994590
Nunnally, J. C. (1978). Psychometric theory. New York: McGraw-Hill.
Schmitt, N. (1996). Uses and abuses of coefficient alpha. Psychological Assessment, 8(4), 350–353. http://ist-socrates.berkeley.edu/~maccoun/PP279_Schmitt.pdf
Prats, P. (2005). Métodos para medir la satisfacción del cliente. Madrid: AENOR Ediciones.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.