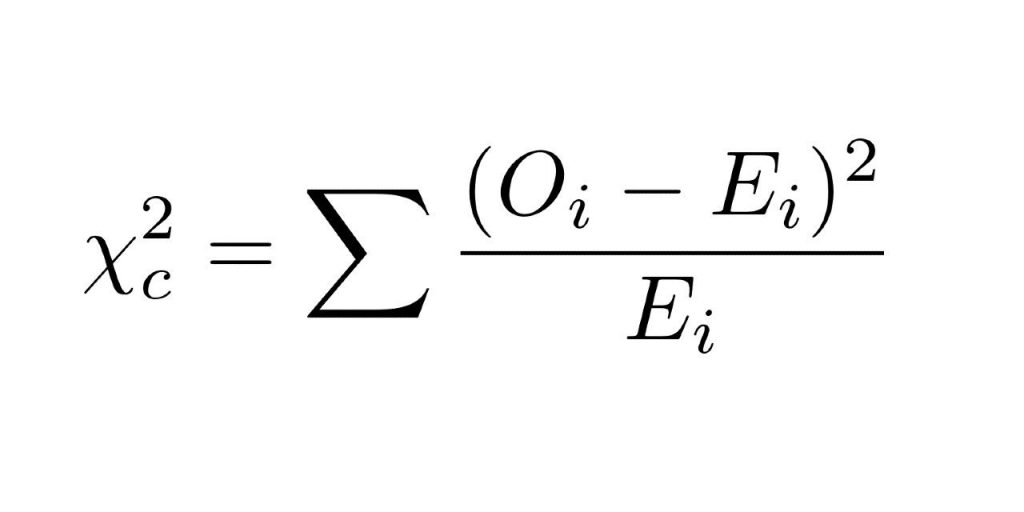El otro día se me ocurrió una idea. Se trataba de aplicar una Tabla de Contingencia y la Prueba χ² de Pearson a las redes sociales. Se me ocurrió hacer una pregunta de cultura general relacionada con un aspecto de la vida del famoso arquitecto Antoni Gaudí. Podemos leer, por ejemplo en Wikipedia, su trágica muerte: «El 7 de junio de 1926 Gaudí se dirigía a la iglesia de San Felipe Neri, que visitaba a diario para rezar y entrevistarse con su confesor, mosén Agustí Mas i Folch; pero al pasar por la Gran Vía de las Cortes Catalanas, entre las calles Gerona y Bailén, fue atropellado por un tranvía, que lo dejó sin sentido. Siendo tomado por un mendigo, al ir indocumentado y a causa de su aspecto descuidado, con ropas gastadas y viejas, no fue socorrido de inmediato, hasta que un guardia civil paró un taxi que lo condujo al Hospital de la Santa Cruz. Al día siguiente lo reconoció el capellán de la Sagrada Familia, mosén Gil Parés, pero ya era tarde para hacer nada por él. Murió el día 10 de junio de 1926, a los 73 años de edad, en la plenitud de su carrera«.
Todo el que está interesado en la arquitectura normalmente ha conocido parte de la obra de este genial arquitecto, incluso ha visto documentales, leído libros o artículos que hablan de él. Su trágica muerte puede considerarse como un hecho que llama la atención, por tanto, puede ser una buena pregunta de cultura general.
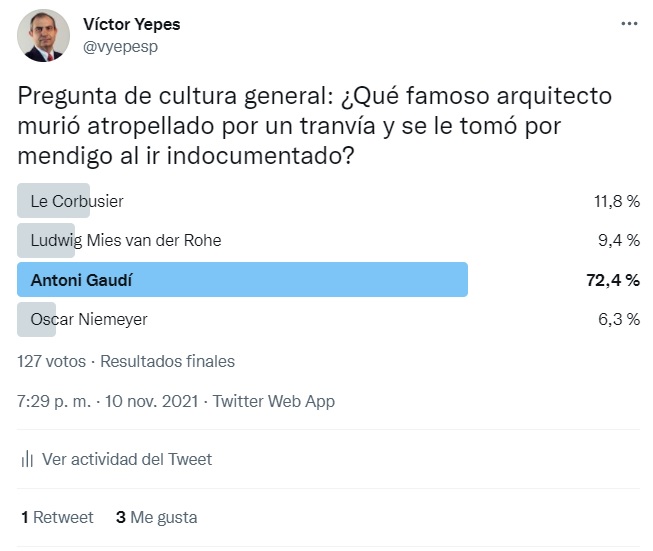
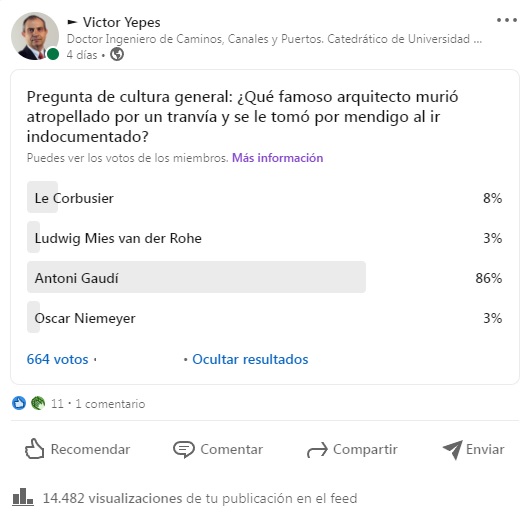
El caso es que hice una pequeña encuesta en redes sociales, tanto en Twitter como en LinkedIn. Con los datos que he obtenido se pueden hacer varias reflexiones e, incluso, un análisis estadístico. Los resultados os los pongo en las figuras siguientes:
Como podéis observar, en ambas redes sociales la mayoría abrumadora ha respondido la opción correcta, que es Antoni Gaudí. Sin embargo, es curioso observar algunas cosas:
a) Para el mismo periodo de respuesta, en LinkedIn ha conseguido casi seis veces más de respuestas que en Twitter. Eso a pesar de que en Twitter tengo unos 21500 seguidores y en LinkedIn poco más de 11000. Se podría interpretar como que la red LinkedIn es más profesional y especializada que Twitter, lo cual era algo que ya sabíamos de antemano.
b) Lo curioso es que en Twitter este tuit tuvo 968 impresiones y solo 112 contestaron la encuesta (11,6%), pero en LinkedIn hubo 14482 visualizaciones y solo votaron 664 (4,6%). El resto, o no estaba interesado, o no sabía la respuesta. Por tanto, en LinkedIn hubo más impacto, pero un porcentaje menor de respuestas.
c) En LinkedIn ha sido el porcentaje de aciertos (86%) superior al de Twitter (72,4%), lo cual puede reforzar la conclusión anterior sobre la profesionalidad y especialización de estas dos redes sociales.
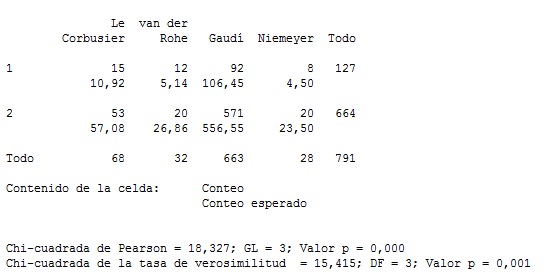
d) Con los datos anteriores se puede construir una Tabla de Contingencia (ver tabla siguiente). En esta tabla se puede ver que la respuesta esperada de la solución correcta en Twitter es de 106,45 aciertos, frente a los 92. En cambio, en LinkedIn la respuesta correcta esperada (556,55) es inferior a la realmente obtenida (571).
e) Por último, haciendo la Prueba χ² de Pearson, el p-valor obtenido con MINITAB es de 0,000. Como p-valor > 0,05, existen evidencias sólidas para rechazar la hipótesis nula de que las proporciones entre las poblaciones son las mismas. Es decir, diremos que las redes sociales analizadas no son homogéneas.
Es evidente que esta pequeña prueba no sirve para nada más que para lo que he comentado. Para una sola pregunta y para un solo caso, sí que se han visto diferencias significativas entre Twitter y LinkedIn. Pero no se puede generalizar. Para ello se podría proponer otro tipo de cuestionarios, con una mejor estratificación muestral y con mayor amplitud de miras. Pero eso es otra historia. Igual hasta hay posibilidad de hacer un trabajo de investigación sobre este tema.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.