En el análisis de estructuras de los ámbitos de la ingeniería civil y mecánica se presentan numerosas situaciones en las que se aplican cargas en regiones localizadas de un cuerpo elástico. En estos casos, el estudio detallado del comportamiento del esfuerzo y la deformación cerca de los puntos de carga puede resultar complejo o innecesario si el interés del análisis se centra en regiones alejadas de estas zonas. Para abordar este tipo de problemas de forma más eficiente, se recurre al principio de Saint-Venant, formulado por el científico francés Adhémar Jean Claude Barré de Saint-Venant en 1855.
El principio de Saint-Venant se basa en una observación fundamental:
Los esfuerzos y deformaciones unitarias producidos en puntos del cuerpo que están suficientemente alejados de la zona donde se aplica una carga son prácticamente iguales a los que se producirían si en su lugar se aplicara otra distribución de cargas estáticamente equivalente sobre la misma región.
En otras palabras, si dos sistemas de fuerzas generan la misma resultante y el mismo momento resultante en una región concreta del cuerpo, entonces su efecto sobre el campo de tensiones y deformaciones a cierta distancia de esa zona será prácticamente el mismo, independientemente de cómo se distribuya la carga exactamente en esa región.
Este principio también implica que los efectos locales, como concentraciones de esfuerzo o distribuciones complejas cerca de los apoyos o puntos de aplicación, se disipan progresivamente hacia el interior del cuerpo y dejan de tener influencia significativa en zonas alejadas.
Desde el punto de vista físico, el principio de Saint-Venant se basa en la capacidad de los materiales elásticos para redistribuir las tensiones internamente. Las cargas aplicadas en una pequeña región producen un campo de tensiones localmente complejo, pero este campo tiende a estabilizarse a medida que nos alejamos de la fuente de perturbación.
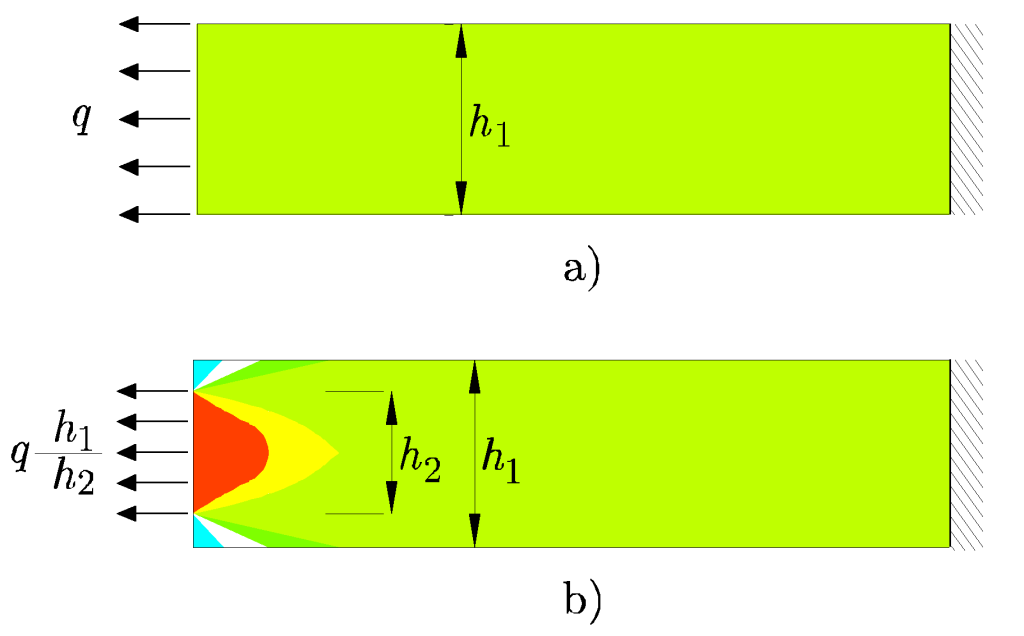
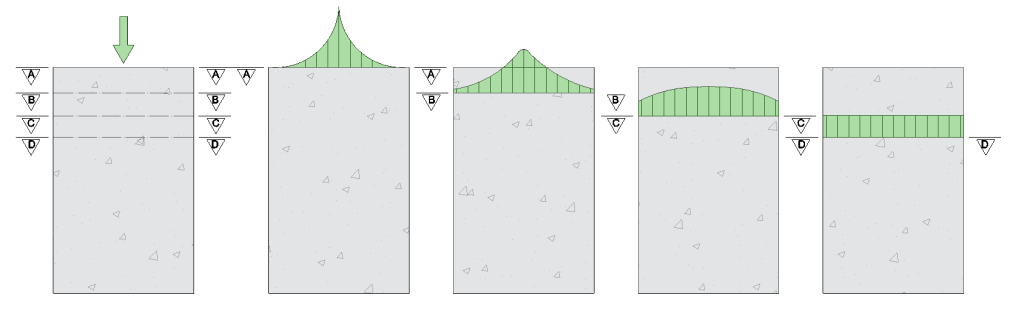
Por ejemplo, una carga puntual aplicada sobre una estructura provoca, en teoría, una tensión infinita en su punto de aplicación. Para modelar correctamente esta situación, se reemplaza por una distribución continua de carga sobre una pequeña superficie, de modo que se mantiene el equilibrio estático (misma fuerza y mismo momento). Aunque el reparto de tensiones es diferente cerca del punto de carga, el comportamiento del cuerpo será el mismo en regiones lejanas para ambas situaciones.
Este principio tiene consecuencias directas en el análisis estructural, ya que permite simplificar el estudio de esfuerzos y deformaciones sin necesidad de conocer con detalle la forma real de aplicación de las cargas. Algunas aplicaciones clave son:
- Idealización de cargas complejas: las cargas concentradas, como ruedas, apoyos o uniones, pueden modelarse como distribuciones equivalentes sin alterar el análisis global.
- Diseño por tramos o secciones: el comportamiento de una viga o columna puede estudiarse por secciones lejos de los apoyos sin considerar la distribución exacta de las reacciones.
- Análisis numérico (por el método de elementos finitos): en zonas alejadas de las condiciones de contorno, no es necesario modelar con alta precisión el contacto o la geometría de la carga.
En general, esta «distancia suficiente» a partir de la cual se puede aplicar el principio con seguridad depende de las dimensiones características del cuerpo. En el caso de las vigas, suele ser de una a dos veces la altura de la sección transversal.
Para facilitar la comprensión, puede resumirse de la siguiente manera:
Al estudiar la distribución de esfuerzos en un cuerpo, si nos situamos en una sección suficientemente alejada de los puntos de aplicación de la carga, no necesitamos conocer la forma exacta en que se aplicaron esas cargas.
Lo relevante es que cualquier otra carga aplicada en la misma región y que sea estáticamente equivalente generará en esa sección los mismos esfuerzos y deformaciones unitarias. En consecuencia, los efectos locales se «suavizan» con la distancia y, en las zonas alejadas, predomina el equilibrio global de fuerzas.
A pesar de su utilidad, el principio de Saint-Venant no debe aplicarse en ciertas condiciones, como por ejemplo:
- Análisis de tensiones cerca de puntos de carga o apoyos, donde los efectos locales no se han disipado.
- Situaciones donde se presentan fenómenos como fatiga, fisuración o plastificación, que dependen críticamente de concentraciones de tensiones.
- Cuerpos donde la distancia entre la zona de carga y la zona de interés es comparable a las dimensiones del sólido, por lo que no puede garantizarse la atenuación de efectos.
Tampoco es válido en materiales no elásticos o no lineales, donde la redistribución interna del esfuerzo no sigue el comportamiento descrito por la teoría elástica clásica.
El principio de Saint-Venant es un pilar fundamental en la formulación de modelos estructurales simplificados. Su aplicación permite al ingeniero centrarse en el análisis global sin necesidad de resolver problemas localmente complejos cerca de las cargas o apoyos.
En resumen, este principio nos recuerda que:
- Los detalles locales importan poco a gran distancia, siempre que se conserve el equilibrio estático.
- Las cargas reales pueden sustituirse por distribuciones ideales equivalentes en regiones alejadas.
- La disipación de los efectos locales permite resolver problemas estructurales con mayor eficiencia sin sacrificar precisión en la mayoría de los casos prácticos.
Os dejo algunos vídeos explicativos. Espero que os sean de interés.
Referencias:
- Berrocal, L. O. (2007). Resistencia de materiales. McGraw-Hill.
- Hibbeler, R. C. (2006). Mecánica de materiales. Pearson educación.
- Rui-Wamba, J. (2020). Teoría unificada de estructuras y cimientos: Una mirada transversal. Reverte.
