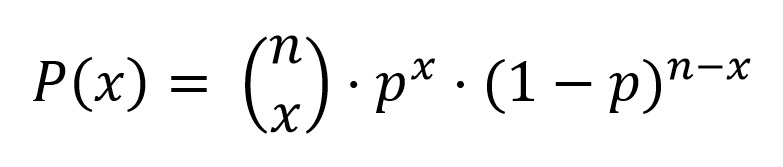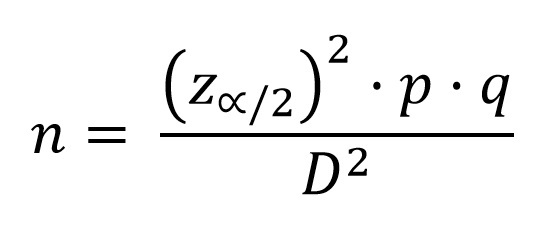Las observaciones instantáneas constituye un procedimiento de medición del trabajo que, junto con el cronometraje, permite determinar los tiempos improductivos y sus causas, eliminándolas mediante su análisis. Se emplea como auxiliar del estudio de métodos para eliminar o disminuir el tiempo de trabajo. El cronometraje es más apropiado para trabajos muy sistematizados y repetitivos, efectuados por una o pocas unidades de recurso. En cambio, las observaciones instantáneas cubre el resto de los escenarios posibles, como trabajos poco sistematizados, con ciclos largos o realizados por numerosos recursos.
Las observaciones instantáneas se basan en comprobar si, en un momento dado, un recurso se encuentra trabajando o parado. Se puede estimar el tiempo de trabajo y el de parada, así como su error estadístico basándose en la distribución binomial de probabilidad. Se puede ejecutar una pasada si observamos a un conjunto de recursos y anotamos para cada uno de ellos su situación de trabajo o parada. Para planificar correctamente las observaciones, se debería garantizar que todas las actividades sean observadas un número de veces proporcional a su duración.
Detengámonos un momento en el fundamento estadístico del método. Supongamos que p es la fracción del tiempo en el que un recurso presenta una característica. Por ejemplo, si p=15% puede significar que, del tiempo total de permanencia de una máquina en una obra, el 15% del tiempo se encuentra parada. Si extraemos n elementos de la población infinita de posibilidades en las que una máquina puede estar parada en una proporción p en una obra, la probabilidad de que x máquinas se encuentren paradas sería la siguiente:
Si en la distribución binomial se cumple que n·p>15, entonces la distribución binomial —que es discontinua— se puede aproximar a la distribución normal —que es continua—.
Ahora lo que nos interesa es conocer el tamaño de la muestra n para proporciones en una población infinita. Para calcular este tamaño de muestra, antes debemos especificar el nivel de confianza con el que se desea realizar la estimación y el margen de error máximo tolerable D. De esta forma, se espera trabajar con una muestra que sea representativa y que las estimaciones sean consistentes. La expresión que utilizaremos será la siguiente:
Aquí os dejo una tabla que relaciona el nivel de confianza con los las variables utilizada en la fórmula anterior:
| Nivel de confianza | α | Z α/2 | (Z α/2)2 |
| 99% | 0,01 | 2,576 | 6,636 |
| 95% | 0,05 | 1,960 | 3,842 |
| 90% | 0,10 | 1,645 | 2,706 |
| 80% | 0,20 | 1,280 | 1,638 |
| 50% | 0,50 | 0,674 | 0,454 |
También os dejo un vídeo explicativo y un problema resuelto.
Referencia:
YEPES, V. (2015). Coste, producción y mantenimiento de maquinaria para construcción. Editorial Universitat Politècnica de València, 155 pp. ISBN: 978-84-9048-301-5.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.