En la era del Big Data, tenemos, casi instintivamente, la idea de que más información siempre es mejor. Acumular más datos parece el camino directo hacia decisiones más inteligentes, resultados más fiables y una certeza casi absoluta. Creemos que si medimos algo diez, cien o mil veces, nuestra comprensión del fenómeno será inevitablemente más profunda y precisa.
Sin embargo, en el ámbito de la experimentación científica rigurosa, esta intuición puede resultar peligrosamente engañosa. Existe un concepto fundamental que a menudo se pasa por alto y que es mucho más importante que la mera cantidad de mediciones. No se trata de cuántos datos se recogen, sino de cómo se recogen. La estructura de un experimento es clave para su eficacia.
En este artículo se desglosan tres ideas clave del diseño experimental que revelan por qué la arquitectura de un estudio es más relevante que la cantidad de datos brutos. Prepárate para descubrir el secreto del éxito en los experimentos.
1. ¿Quién es nuestro protagonista? La unidad experimental.
Todo experimento comparativo tiene una estrella principal, un elemento central en torno al cual gira toda la acción. No se trata del tratamiento aplicado ni de la variable medida, sino de la unidad experimental (UE). Pero, ¿qué es exactamente?
Una unidad experimental es el elemento más pequeño al que se puede asignar un tratamiento de forma completamente independiente. Es la pieza fundamental sobre la que se realizan las mediciones para determinar qué ocurre. Piensa en ella como el «sujeto» de tu experimento.
Los ejemplos concretos ayudan a entenderlo mejor:
- En la agricultura, si quieres comparar dos tipos de fertilizantes, la unidad experimental podría ser una parcela de terreno de un tamaño determinado.
- En un estudio médico, la unidad experimental suele ser un paciente.
- En entomología, podría tratarse de un insecto concreto o incluso de una colonia entera.
La clave está en que la definición de la unidad experimental depende de los objetivos de la investigación. Se trata de la pieza fundamental sobre la que se construye toda la comparación. Definir esta unidad es el primer paso, pero el verdadero desafío surge cuando empezamos a tomar mediciones en ella, lo que nos lleva a una de las trampas más comunes de la ciencia.
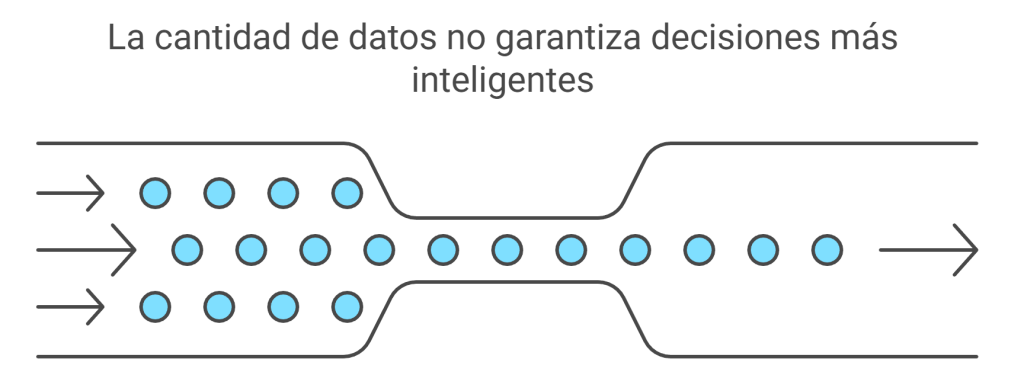
2. El espejismo de los «diez datos»: por qué medir más no siempre es medir mejor.
Esta es una de las confusiones más frecuentes. A menudo, en una unidad experimental podemos tomar varias mediciones. A estos subelementos los llamamos «unidades muestrales». Por ejemplo, en una parcela de terreno (la UE) podríamos analizar diez plantas distintas (las unidades muestrales).
Parecería que tenemos diez datos, ¿verdad? Técnicamente, sí, pero no son lo que parecen. Hay una regla de oro en el diseño experimental que lo cambia todo:
Las unidades muestrales dentro de una misma unidad experimental deben recibir el mismo tratamiento. Por ello, la asignación del tratamiento a estas unidades muestrales no es independiente entre sí.
Esto tiene unas implicaciones enormes. Las diez plantas de la misma parcela son como hermanos que crecieron en la misma casa. Comparten el mismo terreno, la misma cantidad de luz solar y la misma cantidad de agua. Medirlas por separado no es lo mismo que entrevistar a diez personas de distintas partes de la ciudad. Su similitud y su falta de independencia significan que no se obtienen diez puntos de vista únicos, sino diez variaciones sobre el mismo punto de vista. Confundir estas muestras con diez unidades experimentales independientes es uno de los errores más frecuentes al interpretar resultados.
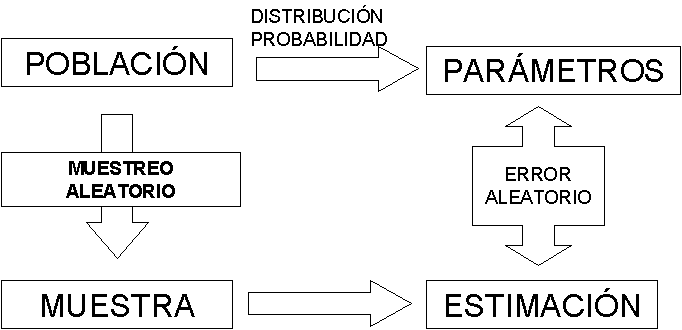
Entonces, si multiplicar las muestras en una misma parcela no aumenta la fiabilidad, ¿cómo podemos estar seguros de que nuestro tratamiento funciona? La respuesta no consiste en acumular más mediciones, sino en comprender y medir correctamente el «ruido» del sistema.
3. Abraza el ruido: por qué el «error experimental» es tu mejor aliado.
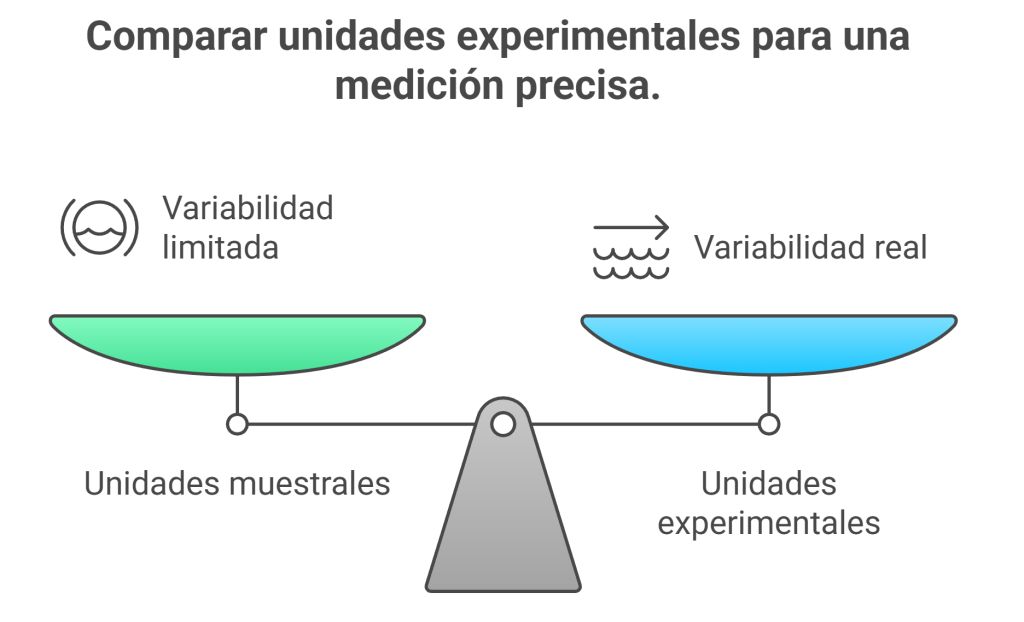
La palabra «error» tiene una connotación negativa, pero en la ciencia el error experimental es tu mejor aliado. No se refiere a una equivocación ni a un fallo de medición. Se trata simplemente de la variabilidad natural entre las unidades experimentales. Es el «ruido» de fondo inevitable del sistema que estás estudiando. Dos pacientes nunca son idénticos ni dos parcelas de terreno son clones perfectos.
Para medir este «ruido» natural, necesitamos comparar manzanas con manzanas. Por eso la unidad experimental (Idea 1) es tan importante. La pequeña variación entre diez plantas de la misma parcela (las unidades muestrales de la idea 2) no nos dice nada sobre la variabilidad natural entre parcelas. El verdadero error experimental solo puede medirse comparando las diferencias entre múltiples parcelas completas que recibieron el mismo tratamiento.
La diferencia de altura entre dos plantas situadas a pocos centímetros entre sí en la misma parcela bien fertilizada será mínima. Esta pequeña variación no nos dice nada sobre la eficacia del fertilizante en general, especialmente si lo comparamos con otra parcela que, por su composición natural, presenta un suelo completamente diferente. La variación entre las parcelas es lo que constituye el verdadero desafío. La esencia de un buen experimento consiste en determinar si el efecto del tratamiento es mayor que la variabilidad natural. Sin una medición honesta de este error, es imposible sacar conclusiones válidas.
Conclusión: mirar más allá de los números.
La validez de un experimento no depende de la cantidad de mediciones, sino de la correcta definición, asignación y comparación de sus unidades experimentales. Es la estructura, no el volumen, lo que permite separar la señal del ruido.
La próxima vez que leas sobre un nuevo estudio, ignora por un momento el deslumbrante número de mediciones. En su lugar, busca a la verdadera protagonista: la unidad experimental. Pregúntate cómo la definieron los investigadores y cómo la utilizaron para medir el ruido de fondo. Esa es la diferencia entre una montaña de datos y un verdadero descubrimiento.
En esta conversación puedes descubrir alguna de las ideas de este artículo.
También puedes ver este vídeo, donde se recogen los conceptos más interesantes del tema.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
