
Cuando se utiliza un modelo de toma de decisiones multicriterio tal y como el AHP (Proceso Analítico Jerárquico), una de las dudas que surgen es saber cómo agregar los juicios de todos los expertos de una forma razonable. Una solución sería la de buscar un consenso de grupo mediante un proceso interactivo con varias rondas de negociación entre los expertos. En este caso, un moderador que no participa en la discusión, sugiere a los responsables de la toma de decisiones que actualicen sus juicios. Sin embargo, a veces es difícil llegar a un acuerdo consensuado (Dong y Saaty, 2014).
En el caso de tener un grupo de expertos homogéneos (coincidencias en formación, trabajo profesional, finalidad de su trabajo, etc.), vamos a basarnos en la media geométrica para agregar los juicios. A pesar de que esta media es menos intuitiva que la aritmética, es una medida menos sensible a los valores extremos que la media de una muestra estadística. Además, la media geométrica es adecuada para calcular variables en porcentaje o índices. Los juicios de las comparaciones pareadas en AHP son ratios, sus valores siempre son positivos, mayores que cero, y algo no menos importante, la media geométrica cumple con satisfacción la propiedad recíproca de las matrices de comparación.
Un ejemplo muy sencillo permite comprobar la reciprocidad con la media geométrica, frente a la media aritmética. Supongamos que con la media aritmética la media de dos juicios con valores de 7 y 9 resultaría en 8, cuyo valor reciproco es 1/8, pero en el otro lado de la matriz obtendríamos un valor de (1/7 + 1/9)/2 = 8/63 lo que difiere del valor esperado de 1/8 para mantener la matriz recíproca. Dejamos al lector la comprobación de que con la media geométrica se mantiene la reciprocidad.
Existen dos formas de agregar los juicios individuales de un grupo de expertos homogéneos:
a) Agregación de prioridades individuales, que transforma vectores de prioridad individuales en un vector de prioridad del grupo (Figura 2).
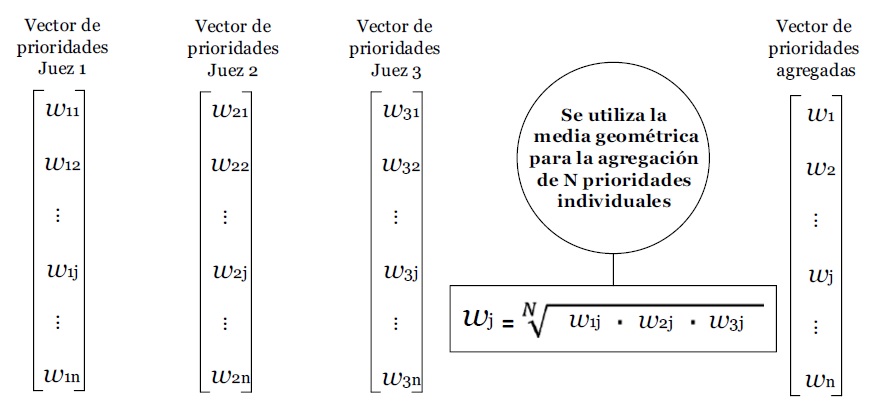
b) Agregación de juicios individuales, que transforma las matrices comparación por pares individuales en una grupal (Figura 3). En este caso, si las matrices individuales tienen una consistencia aceptable, la grupal también suele serlo (Dong y Saaty, 2014).
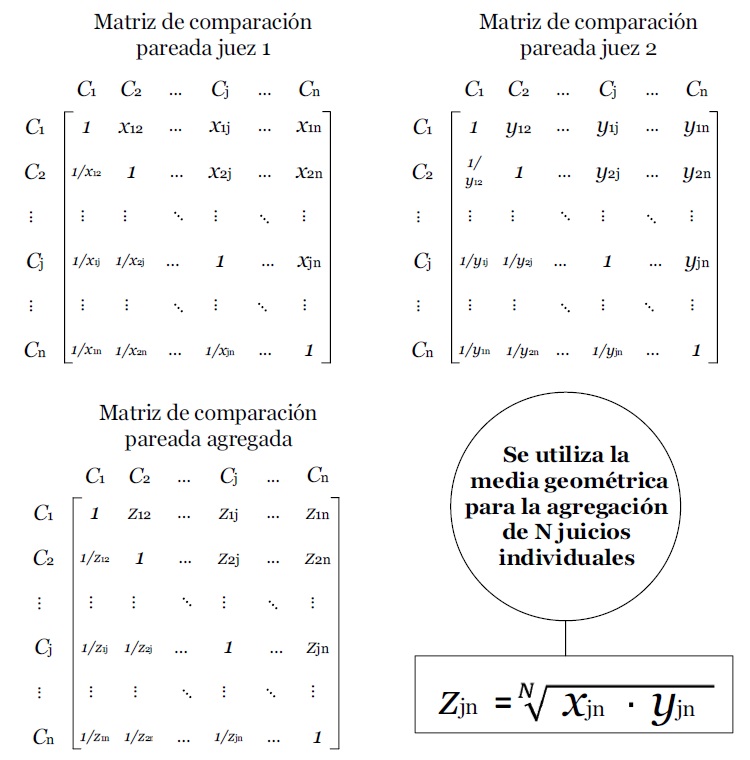
En ambos casos, hay que tener en cuenta que el vector propio resultante del grupo se debe normalizar.
Otro problema sería el de grupos heterogéneos de expertos, que pueden llegar a producir resultados bastante divergentes. En este caso, se suele resolver el problema mediante la Programación por metas extendida (Linares y Romero, 2002). Aunque también es posible acudir a otro tipo de métodos, como la lógica neutrosófica (Navarro et al., 2020; 2021).
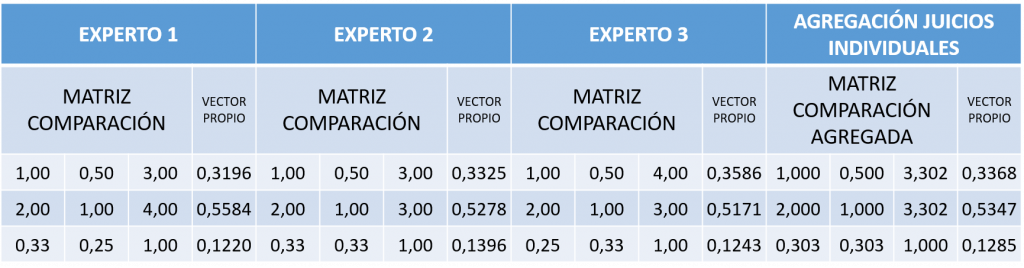
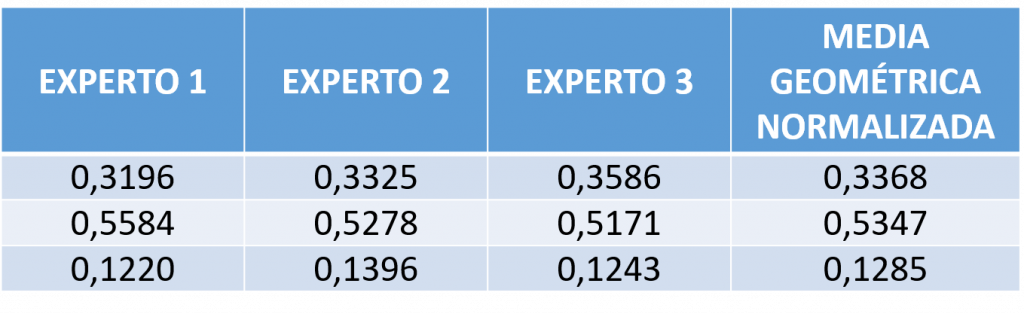
A continuación ponemos un ejemplo de tres expertos homogéneos. En primer lugar vamos a agregar los juicios individuales de tres expertos (Figura 4) y, como método alternativo, agregaremos los vectores propios de cada experto (Figura 5), llegando, en este caso, a un vector propio normalizado que coincide en ambos casos.
Referencias:
AZNAR, J.; GUIJARRO, F. (2012). Nuevos métodos de valoración: modelos multicriterio. Editorial Universitat Politècnica de València.
BERNAL, S.; NIÑO, D.A. (2018). Modelo multicriterio aplicado a la toma de decisiones representables en diagramas de Ishikawa. Universidad Distrital Francisco José de Caldas, Bogotá D.C., 137 pp.
DONG, Q.; SAATY, T. L. (2014). An analytic hierarchy process model of group consensus. Journal of Systems Science and Systems Engineering, 23(3), 362–374. https://doi.org/10.1007/s11518-014-5247-8
LINARES, P., ROMERO, C. (2002). Aggregation of preferences in an environmental economics context: A goal-programming approach. Omega, 30(2), 89–95. https://doi.org/10.1016/S0305-0483(01)00059-7
NAVARRO, I.J.; YEPES, V.; MARTÍ, J.V. (2020). Sustainability assessment of concrete bridge deck designs in coastal environments using neutrosophic criteria weights. Structure and Infrastructure Engineering, 16(7): 949-967. DOI:10.1080/15732479.2019.1676791
NAVARRO, I.J.; MARTÍ, J.V.; YEPES, V. (2021). Neutrosophic completion technique for incomplete higher-order AHP comparison matrices. Mathematics, 9(5):496. DOI:10.3390/math9050496
