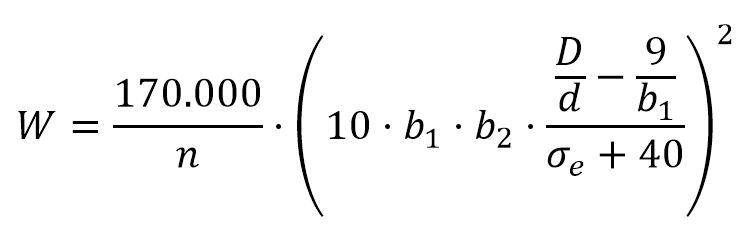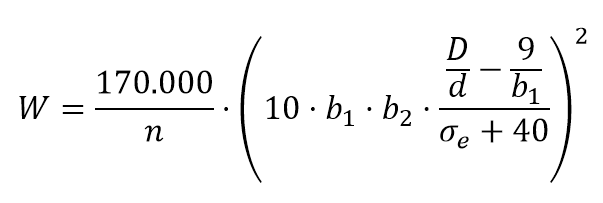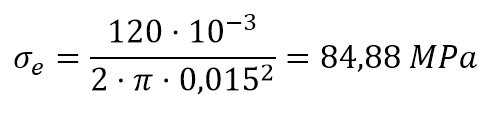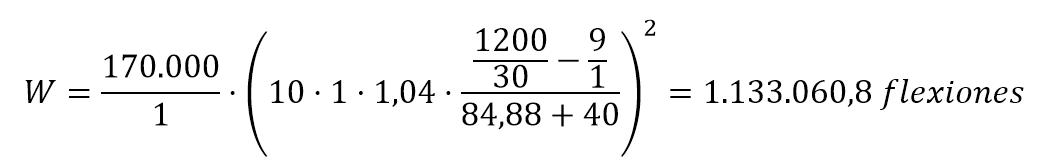duración – El blog de Víctor Yepes

https://blog.bextok.com/guia-cable-de-acero/

Para la máxima duración de un cable, interesa que las solicitaciones se aproximen al límite de fatiga, pero se alejen del límite elástico, evidentemente, para conseguir una mayor seguridad. Que se cumplan ambos requisitos a veces es complicado.

Por eso, para estimar la vida útil de un cable, Gustav Niemann proporciona la siguiente expresión (Larrodé y Miravete, 1996) que intenta aunar estos dos criterios:

Donde W es el número de flexiones sufridas por el cable hasta su rotura (plegado sobre la polea y desplegado); D es el diámetro de la polea (m); d es el diámetro del cable (m); σ_e es el esfuerzo de extensión (MPa). Este valor suele variar entre 30.000 flexiones para el caso de polipastos y 150.000 en el caso de grandes grúas.

El coeficiente n presenta los siguientes valores:

1 flexión en el mismo sentido

1,5 flexión en sentido contrario, cable cruzado

2 flexión en sentido contrario, cable Lang

El coeficiente b₁ depende de la forma de la garganta

para radio de garganta, r = 0,54 d

b₁ = 1 cable cruzado y Lang

para radio de garganta, r = ∞

b₁ = 0,72 cable cruzado

b₁ = 0,65 cable Lang

para garganta en V a 45º

b₁ = 0,72 cable cruzado

b₁ = 0,60 cable Lang

El coeficiente b₂ depende de la forma del cable

b₂ = 1,04 cable cruzado 6 x 37, 1600 MPa

b₂ = 1,11 cable Lang 6 x 37, 1600 MPa

Os dejo un problema resuelto por si os resulta de interés.

PROBLEMA. Se quiere estimar la vida de un cable de un puente grúa que tiene que elevar una carga total de 120 kN. El diámetro de las poleas es de 1200 mm, el cable es cruzado, su resistencia es de 1770 N/mm² y su diámetro es de 30 mm. Se supone que la flexión siempre se realiza en el mismo sentido.

Solución:

Utilizamos la fórmula de Niemann,

donde D = 1200 mm; d = 30 mm, h₁ = 1 (para un radio de garganta r = 0,54d), b₂ = 1,04.

Por otra parte, el esfuerzo de extensión σ_e (MPa) se calcula de la siguiente forma (son dos ramales):

Por tanto,

Este valor es muy superior al límite inferior de 150.000 flexiones requerido para las grandes grúas.

Referencias:

LARRODÉ, E.; MIRAVETE, A. (1996). Grúas. Servicio de Publicaciones, Centro Politécnico Superior, Universidad de Zaragoza, 554 pp.

YEPES, V.; MARTÍ, J.V. (2017). Máquinas, cables y grúas empleados en la construcción. Editorial de la Universitat Politècnica de València. Ref. 814. Valencia, 210 pp.

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El tiempo disponible para realizar cada tarea lo determinan las fechas en que se produce su inicio y su terminación. La duración de una actividad puede reducirse añadiendo recursos adicionales que, desgraciadamente, incrementan su coste. Existe la posibilidad de modificar los recursos asignados a cada tarea para ajustarse a las condiciones más convenientes, según las contingencias que se presenten durante la ejecución de la obra. Estos cambios producen una aceleración o deceleración en la realización de ciertas actividades con el consiguiente aumento o disminución de su coste directo. Se produce, por tanto, una correspondencia entre el coste directo de cada actividad y el tiempo invertido en su ejecución que proporciona la posibilidad de un ajuste costes-tiempos, adaptable a las necesidades de plazo o a la inversión económica del momento.

La duración “normal” de una tarea es aquella que minimiza su coste. En ocasiones, una programación basada en la duración normal puede prolongar excesivamente el trabajo, incrementando la repercusión de los gastos generales de la empresa en la obra. Del mismo modo, es probable exceder el plazo contractual si se programa exclusivamente con duraciones normales. En ambos casos, el jefe de obra tiene la posibilidad de reducir la duración de algunas o todas las actividades para disminuir el plazo total.

Otra aproximación a la estimación de la duración de las tareas es la que propugna el método PERT, y que ya tuvimos la ocasión de explicar en un artículo anterior. No obstante todo lo anterior, y para evitar una estimación “ad hoc” de las duraciones (es decir, la que más convenga), deberíamos fijar la duración de cada tarea en función de los recursos reales que tengamos para acometerlas. Esta práctica nos llevará a estimaciones realistas y deberíamos hacerla en el momento de la confección de la Estructura de Desglose de Trabajos.

Una pequeña introducción a estos conceptos la vamos a ver en el siguiente Polimedia de Alberto Palomares. Espero que os guste.

Referencias:

PELLICER, E.; YEPES, V. (2007). Gestión de recursos, en Martínez, G.; Pellicer, E. (ed.): Organización y gestión de proyectos y obras. Ed. McGraw-Hill. Madrid, pp. 13-44. ISBN: 978-84-481-5641-1. (link)

YEPES, V.; PELLICER, E. (2008). Resources Management, in Pellicer, E. et al.: Construction Management. Construction Managers’ Library Leonardo da Vinci: PL/06/B/F/PP/174014. Ed. Warsaw University of Technology, pp. 165-188. ISBN: 83-89780-48-8.

YEPES, V.; MARTÍ, J.V.; GONZÁLEZ-VIDOSA, F.; ALCALÁ, J. (2012). Técnicas de planificación y control de obras. Editorial de la Universitat Politècnica de València. Ref. 189. Valencia, 94 pp. Depósito Legal: V-423-2012.

YEPES, V. (2015). Coste, producción y mantenimiento de maquinaria para construcción. Editorial Universitat Politècnica de València, 155 pp. ISBN: 978-84-9048-301-5.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Etiqueta: duración

Cálculo de la duración de un cable de acero

¿Cómo se puede estimar la duración de una actividad?