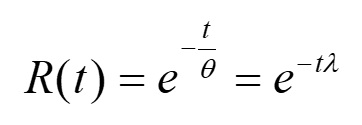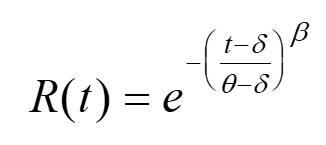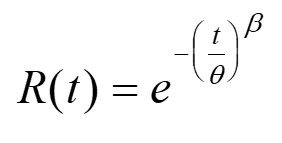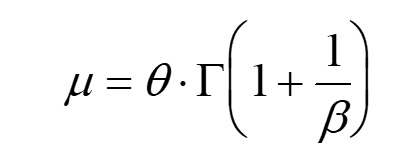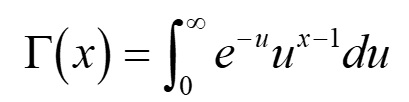Una unidad simple o compuesta, bajo unas condiciones determinadas, puede no completar la misión para la cual estuvo diseñada y, por lo tanto, dar lugar a un fallo. Los mecanismos llevan a un elemento al fracaso se deben a deterioros por desgaste, al medio ambiente o al azar. Los fallos pueden clasificarse en dos categorías:
- Fallo de parada o avería: causa el cese de una función.
- Fallo de deterioro: afecta a la calidad o causa deterioro funcional. El equipo sigue trabajando, pero las imprecisiones y otros tipos de degradación funcional crean defectos en el producto acabado o afecta a su productividad.
El concepto de fiabilidad se encuentra relacionado con el de disponibilidad y el de mantenimiento. En efecto, las máquinas no son infalibles, y por tanto para aumentar su tiempo disponible en las obras se requiere una correcta política de reparación y mantenimiento (Figura 1).
Se define la fiabilidad como la probabilidad de que una unidad funcione satisfactoriamente en un intervalo de tiempo determinado, sin que sufra interrupciones de su trabajo por fallo de alguno de sus componentes, siempre que dicho dispositivo se emplee en condiciones establecidas.
La fiabilidad se relaciona con el promedio de horas entre averías, o tiempo medio entre fallos (TMEF), definiéndose para un equipo reparable como la relación del número de horas trabajadas en un intervalo de tiempo y el número de averías sufridas en ese mismo período.
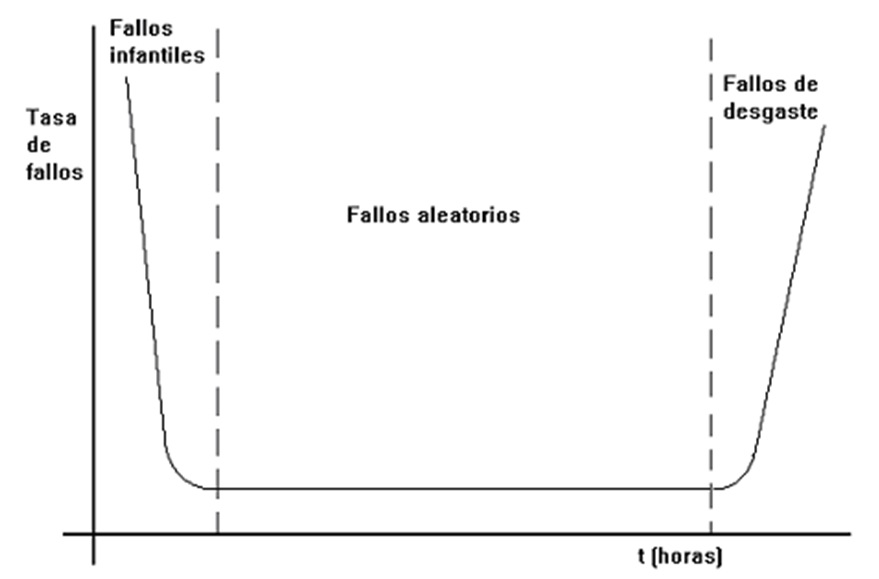
Los equipos siguen a menudo un modelo de fallo similar. La curva de fiabilidad de una máquina representa la evolución de la tasa de fallos de una máquina a lo largo del tiempo. También recibe el nombre de “curva de la bañera”, por su forma. En dicha curva aparecen tres zonas que se diferencian por la frecuencia de los fallos y su causa (ver Figura 2):
1.- Período de mortalidad infantil o de fallos prematuros. Caracterizada por una tasa de fallos elevada que disminuye rápidamente con el tiempo. Las causas de los fallos normalmente se deben a errores de diseño, de fabricación, de utilización u otras causas identificables, que una vez resueltas no suelen repetirse. Los fallos precoces ocurren durante la fase de rodaje de la máquina.
2.- Período de tasa de fallos constante o vida útil. Los fallos aparecen de forma aleatoria y accidental debido a limitaciones del diseño más los percances causados por el uso o por un mal mantenimiento. Es aconsejable limitar la utilización de las máquinas a este período. Para reducir la cuota de fallos durante la vida útil, se debería rediseñar el equipo.
3.- Período de desgaste. Caracterizado por deterioros crecientes con el tiempo, debidos a la vejez y terminación de la vida útil del equipo. Para reducir la tasa de fallos se requiere el reemplazamiento preventivo de los componentes gastados, antes de un incidente catastrófico, llegando incluso a la renovación completa del equipo.
Se podría alargar al máximo la vida útil de un equipo:
- Mediante un envejecimiento preventivo de las máquinas o sus componentes. Al someter a una unidad a un funcionamiento preliminar se eliminan los fallos prematuros. Constituye la “purga” de un elemento antes de instalarlo en un sistema.
- Mediante la sustitución preventiva, reemplazando las unidades o componentes al acabar su vida útil, sin esperar a su avería, evitando que se produzcan fenómenos masivos de mortalidad por envejecimiento.
Cuando la tasa de fallos es constante, la ocurrencia de un fallo es imprevisible, es decir, es independiente de la vida acumulada de la unidad. En este caso, el tiempo libre de fallos se distribuye exponencialmente, dependiendo la fiabilidad únicamente de la duración de la misión del elemento. Estas hipótesis sustentan el denominado modelo exponencial de la fiabilidad que, si bien no es estrictamente exacto para las máquinas, debido a sus desgastes, es un modelo muy utilizado por su sencillez:
donde
R(t) = Probabilidad de funcionamiento libre de fallos durante un período de tiempo igual o mayor que t.
e = 2.718
t = Un período especificado de funcionamiento libre de fallos.
θ = Tiempo medio entre fallos o “vida media”.
λ = Tasa de fallos (la inversa de q).
Se comprueba que la vida media es superada solo por el 36,8% de las unidades del mismo tipo en funcionamiento, pues R(1/λ)=0,368.
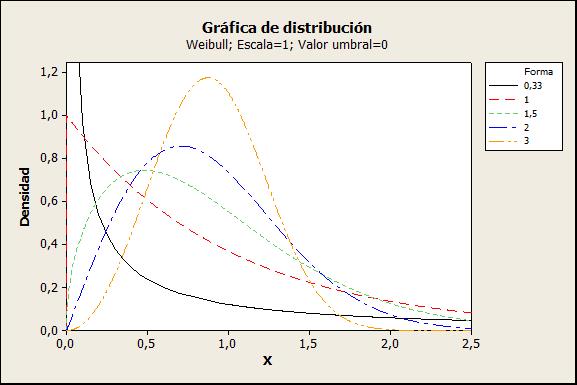
Una generalización del modelo exponencial es la función de Weibull, para situaciones con tasa de fallo variable, siendo adecuado en fases de fallos precoces y de envejecimiento:
donde
δ = vida mínima (>= 0)
θ = vida característica (> δ)
β = parámetro de forma (> 0)
con frecuencia se toma δ = 0, con lo cual:
β = 1 con una cuota de fallos constante. Si β <1 la tasa de fallos disminuye con el tiempo, correspondiendo con la etapa de mortalidad infantil. Si β >1, la tasa de fallos aumenta con el tiempo, recayendo con el período de desgaste. Para β =3,5 la distribución de Weibull se aproxima mucho a la normal.
La vida media adquiere con el modelo de Weibull la siguiente expresión:
donde
De la función de distribución de Weibull resulta, por desarrollo matemático que la tasa de fallos sería:
donde λ(t) indicaría qué porcentaje de unidades sobreviven hasta la duración t, se avería en el intervalo siguiente (t+dt).
Referencias:
YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente nº 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.
YEPES, V. (2015). Coste, producción y mantenimiento de maquinaria para construcción. Editorial Universitat Politècnica de València, 155 pp. ISBN: 978-84-9048-301-5.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.