 YEPES, V.; MEDINA, J.R. (2006). Big-Bang: Un nuevo algoritmo aplicado a la optimización de redes de transporte del tipo VRPTW. Actas del VII Congreso de Ingeniería del Transporte CIT-2006. Libro CD, 8 pp. Ciudad Real, 14-16 de junio. ISBN: 84-689-8341-1.
YEPES, V.; MEDINA, J.R. (2006). Big-Bang: Un nuevo algoritmo aplicado a la optimización de redes de transporte del tipo VRPTW. Actas del VII Congreso de Ingeniería del Transporte CIT-2006. Libro CD, 8 pp. Ciudad Real, 14-16 de junio. ISBN: 84-689-8341-1.
RESUMEN
La ponencia presenta un procedimiento de optimización económica de rutas de reparto con flotas de vehículos heterogéneas y horarios de servicio flexibles VRPHESTW. Para ello se presenta una nueva heurística, denominada “Big-Bang” basada en la modificación gradual de la variable espacial donde se ubican los nodos que representan a los clientes. La simulación de esta heurística de relajación consiste en reducir la velocidad de todos los vehículos, que al principio es muy alta para estabilizarse al final en su verdadera magnitud. El algoritmo emplea para explorar el espacio de soluciones una búsqueda probabilista en entornos variables con una aceptación de máximo gradiente. El algoritmo propuesto encuentra soluciones de elevada calidad, con la ventaja de poder utilizar otros procedimientos de búsqueda local que resulten más eficientes que el de máximo gradiente (algoritmo del solterón, aceptación por umbrales, búsqueda tabú, etc.).
- INTRODUCCIÓN
La asignación de rutas de reparto a una flota de vehículos “Vehicle Routing Problem” (VRP) constituye un problema habitual en las empresas dedicadas a la distribución de bienes o personas que conlleva un impacto económico, social y medioambiental importante. Sin embargo, los problemas de optimización que representan numerosas situaciones reales sólo pueden resolverse mediante procedimientos aproximados debido a su elevada complejidad intrínseca (ver Ball et al., 1995).
En las últimas décadas se han aplicado una gran variedad de técnicas para optimizar el problema de las rutas con horarios de servicio “vehicle routing problem with time windows” (VRPTW), tanto con heurísticas de construcción de soluciones (ver Solomon, 1987) o de mejora (ver Potvin y Rousseau, 1995), como metaheurísticas (ver Homberger y Gehring, 2005; Russell y Chiang, 2006). Sin embargo, son escasas las publicaciones que abordan la optimización con modelos más cercanos a la realidad incorporando horarios de servicio flexibles “vehicle routing problem with soft time windows” (VRPSTW) (ver Taillard et al., 1997), flotas heterogéneas de vehículos “vehicle routing problem with a heterogeneous fleet of vehicles” (VRPHE) (ver Gendreau et al., 1999), o ambas “vehicle routing problem with a heterogeneous fleet of vehicles and soft time windows” (VRPHESTW) (ver Yepes y Medina, 2002, 2004, 2006).
Además, los problemas reales de rutas difieren significativamente de los problemas teóricos. En efecto, la optimización jerárquica empleada habitualmente en la literatura (donde las mejores soluciones son las que, en primer lugar, presentan un menor número de rutas; y posteriormente, una menor distancia recorrida por todos los vehículos), no representa adecuadamente los costes reales de las empresas ni sus políticas de tarifas. Yepes (2002) indicó la trascendencia de utilizar una función objetivo de tipo económico para resolver estos problemas ante cambios en los escenarios de tarifas y costes. Asimismo, las restricciones legales y sociales, así como la calidad del servicio también se deben incluir dentro de una función objetivo de tipo económico, que contemple los ingresos y los costes de las operaciones de transporte (Medina y Yepes, 2003).
En la ponencia se presenta una nueva heurística basada en la modificación gradual de la variable espacial donde se ubican los nodos que representan a los clientes, y que se ha denominado “Big-Bang”. Esta estrategia de relajación, a su vez, se anida en una variante de la búsqueda en entornos variables “Variable Neighborhood Search” (VNS) (ver Mladenovic y Hansen, 1997) apoyada en la elección probabilista de un operador distinto en cada movimiento, empleada con éxito en el trabajo de Yepes y Medina (2006). Todo ello se ensaya con un problema de rutas del tipo VRPHESTW donde, además, se emplea una función objetivo de tipo económico, unas jornadas laborables con distintos costes y con tiempos de viaje dependientes del tiempo de acceso y alejamiento a cada nodo (congestión, tráfico, etc.).
- EL ALGORITMO BIG-BANG
El algoritmo Big-Bang que se propone parte de la siguiente idea: Si todos los vehículos tuviesen una velocidad mayor a la real, dicho fenómeno se podría interpretar como que los clientes se encuentran en un espacio donde, físicamente, las distancias fuesen menores. Un procedimiento de búsqueda encontraría un óptimo local en este escenario favorable a la reducción del número de vehículos. Si se desciende escalonadamente la velocidad, y en cada caso se encuentra su óptimo local, probablemente el nuevo óptimo sería similar al anterior, siempre que la disminución fuera suficientemente suave. Esta relajación de la velocidad se interrumpiría en el último escalón, donde el óptimo local encontrado satisfaría la velocidad real de los vehículos. El efecto sería un aumento gradual del espacio físico donde se ubican los clientes, efecto por el cual se ha querido llamar a la heurística algoritmo Big-Bang. En la situación inicial las restricciones fundamentales que condicionan el problema son la capacidad de los vehículos y los horarios de servicio. Al final, la lejanía entre los clientes y el almacén central, son condiciones que se han introducido progresivamente al final de la heurística.
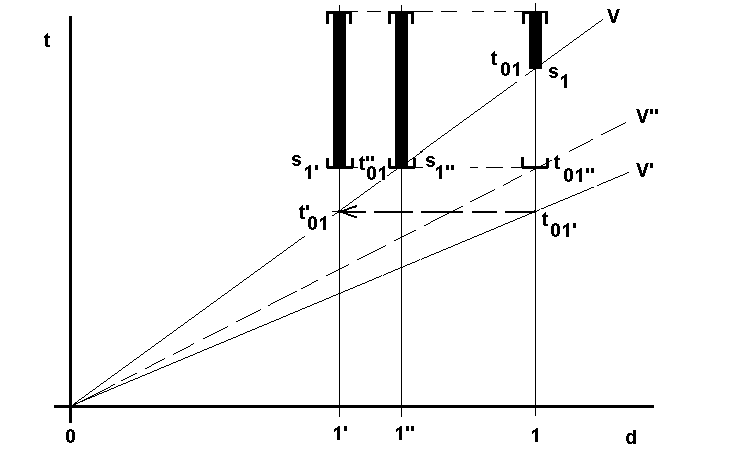
En efecto, un vehículo con una velocidad v llega de 0 a 1 en el instante t01 (ver Figura 1). Se supone, sin perder generalidad, que el tiempo de servicio es nulo. Si la velocidad se incrementase a v’, entonces la llegada ocurriría en t01’. Esta situación equivale a suponer que el nodo, en vez de estar en 1 está más cerca de 0, es decir, en 1’ y la velocidad se mantiene en v. Así, la llegada ocurre en el instante t’01, que es igual al t01’. Por tanto, un aumento en la rapidez de los vehículos es equivalente a un acortamiento físico de las distancias. Sin embargo, las ventanas temporales interfieren en el razonamiento anterior. La existencia de esperas provoca que, aunque la velocidad v’ favorece el acortamiento a la distancia 1’, no es posible iniciar el servicio puesto que lo impide la ventana temporal. La situación equivalente es la representada en la Figura 1 cuando el vehículo circula a una velocidad v’’. En este caso, el acortamiento de distancias a 1’ se ve interrumpido por la limitación en el inicio del servicio a la situación 1’’, donde el inicio del servicio s1’ es coincidente con el s1’’. La conclusión es que el aumento de la rapidez de los vehículos permite relajar las restricciones en las distancias, acortando éstas mientras las limitaciones horarias no lo impidan.
Una de las características más interesantes de esta heurística de relajación consiste en la posibilidad de emplear como procedimientos de búsqueda local en cada escalón de velocidad, metaheurísticas más agresivas de búsqueda que la simple aceptación por umbrales (búsqueda tabú, algoritmo del solterón, cristalización simulada, etc.). En la ponencia que se presenta se ha optado por utilizar una búsqueda de máximo gradiente para comprobar la eficacia intrínseca del algoritmo, para no empañarla con la de otras metaheurísticas que por sí solas resultan, muy eficaces para el problema VRPHESTW (ver Yepes y Medina, 2004).
- DESCRIPCIÓN DE LA METAHEURÍSTICA PROPUESTA
El método presentado consta de dos fases. En la primera se genera una solución inicial mediante una heurística de construcción de rutas específica. Posteriormente se emplea el algoritmo “Big-Bang” basándose en una versión probabilista de la búsqueda por entornos variables “Variable Neighborhood Search” (VNS) (ver Mladenovic y Hansen, 1997) y un criterio de aceptación de máximo gradiente.
3.1 Fase 1: Heurística económica de construcción secuencial de rutas.
Se ha empleado el método de Yepes y Medina (2006) para generar una solución inicial de elevada calidad al problema VRPHESTW. El procedimiento inicia una ruta seleccionando adecuadamente al primer cliente para posteriormente agregar otros mientras se cumplan las restricciones impuestas. Además, se elige el vehículo de mayor capacidad para disminuir en lo posible el número necesario.
3.2 Fase 2: Algoritmo “Big-Bang” con búsqueda probabilista en entornos variables.
El algoritmo que se propone consta de un número M+1 de ciclos de búsqueda local por entornos. Cada ciclo de búsqueda termina con la obtención de un óptimo relativo correspondiente con unas velocidades de los vehículos fijadas para dicho ciclo. En el primer ciclo, la velocidad de los vehículos se amplifica por un factor de incremento D= D1>1. Este factor debe reducirse progresivamente hasta llegar al último ciclo de búsqueda local, en el cual D =DM+1 =1. Para este trabajo, la reducción de la velocidad ha sido lineal con el número de ciclos; sin embargo, se podría adoptar otro tipo de función reductora.
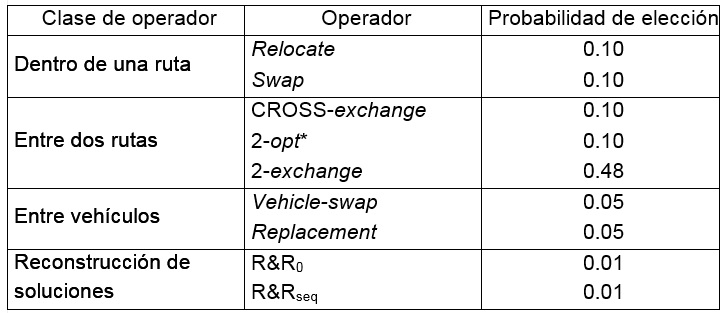
Como técnica de búsqueda local se ha empleado la metaheurística propuesta por Yepes y Medina (2006) para el problema VRPHESTW, de búsqueda por entornos variables basada en la elección probabilística de 9 operadores distintos y un criterio de aceptación por máximo gradiente. Los movimientos elegidos han sido los siguientes:
- Movimientos dentro de una ruta: se emplea el operador relocate (un nodo salta a otro lugar dentro de la ruta) y el swap (dos nodos de la ruta se intercambian entre sí).
- Movimientos entre dos rutas: se utiliza el operador CROSS-exchange (Taillard et al., 1997) y dos casos particulares, el movimiento 2-opt* (Potvin y Rousseau, 1995) y el 2-exchange (Osman, 1993).
- Movimiento de vehículos: vehicle–swap cambia entre sí los vehículos de dos rutas, y replacement sustituye el vehículo de una ruta por otro de la flota que no está utilizándose.
- Reconstrucción de soluciones: R&R0 desconecta un nodo al azar y lo introduce en la posición y ruta más favorable, mientras que R&Rseq rompe la ruta con menor número de nodos, y los reintroduce en la mejor posición y ruta (ver Schirmpf et al., 2000).
La Tabla 1 contiene las probabilidades que tiene cada operador de ser elegido. Dichos valores han ofrecido buenos resultados en experiencias anteriores (ver Yepes, 2002).
- EJEMPLO DE APLICACIÓN AL PROBLEMA VRPHESTW
Se analiza un problema del tipo VRPHESTW denominado HES-A descrito en Yepes y Medina (2004, 2006). Este caso deriva del ejemplo R103 de Solomon (1987), al cual se incorporan horarios flexibles de entrega, flotas heterogéneas y una función económica caracterizada por unos ingresos y unos costes fijos y variables. El lenguaje código utilizado ha sido Visual Basic 6.0 ejecutándose los ejemplos en un ordenador Pentium IV 3.00 GHz.
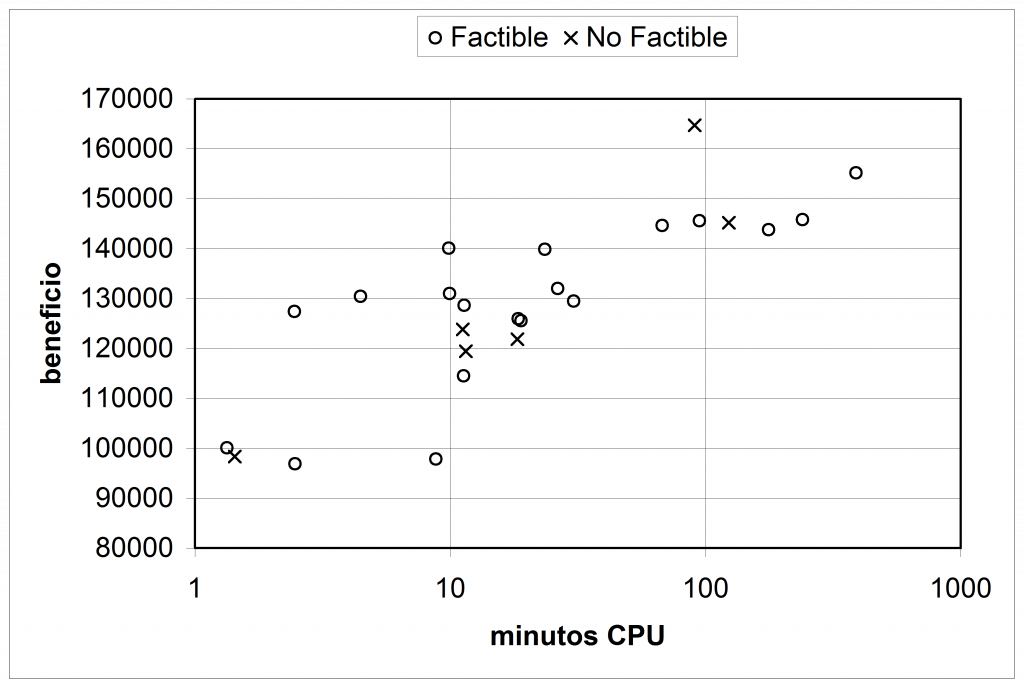
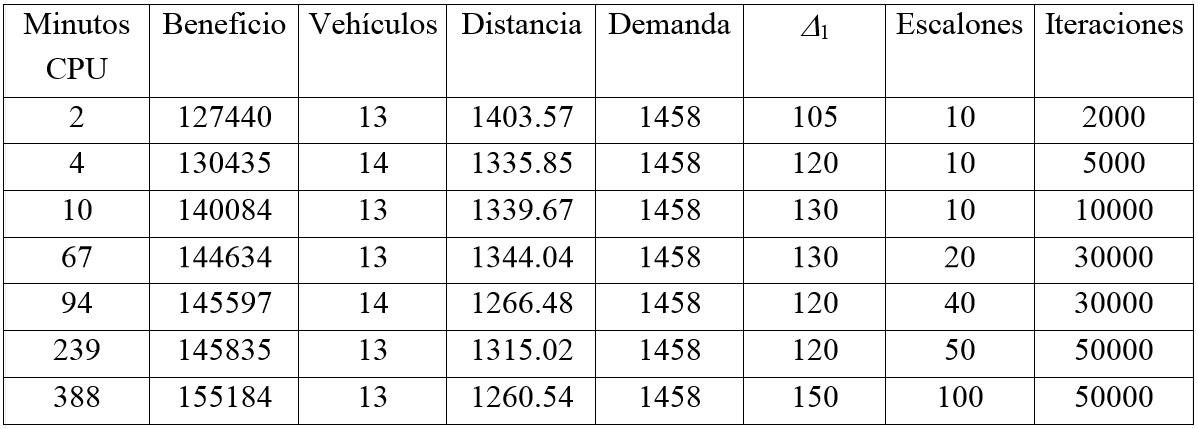
En las Figuras 2 y 3 se representa el beneficio obtenido y el tiempo empleado por la heurística descrita cuando se aplica al problema HES-A. El número de iteraciones empleadas para cada escalón de velocidad ha oscilado entre 1000 y 50000. Los escalones de velocidad ensayados varían entre 3 y 100. La mejor solución encontrada se corresponde con un beneficio de 164752, obtenida para un factor inicial de modificación de la velocidad D1=130, así como 30000 iteraciones en cada uno de los 30 escalones de velocidad considerados. Sin embargo, esta solución no atiende a todos los clientes (sólo el 96.70% de la demanda queda cubierta). La mejor solución que atiende toda la demanda se corresponde con un beneficio de 155184, obtenida para un D1=150, así como 50000 iteraciones en 100 escalones de velocidad. Destacamos cómo el algoritmo es capaz de aumentar el beneficio de las operaciones a costa de renunciar al servicio a determinados clientes. La mejor solución no factible sólo precisa 12 vehículos y recorre 1224.71 unidades de distancia total, frente a los 13 vehículos y las 1260.54 unidades de distancia de la mejor solución factible. Si se pretende servir toda la demanda, bastaría endurecer las penalizaciones en la función objetivo.

En la Tabla 2 se han recogido los valores óptimos en el sentido de Pareto de las soluciones factibles (ver Voorneveld, 2003). Dichos óptimos se corresponden con los valores de mayor beneficio en el menor tiempo de cálculo posible. Se observa que es favorable el aumento del factor de modificación inicial de la velocidad, del número de escalones y del número de iteraciones. Sin embargo, ello comporta un mayor tiempo de cálculo.
El mejor resultado obtenido por esta metaheurística (ver Tabla 3) es inferior al encontrado por el algoritmo del solterón propuesto por Yepes y Medina (2004) para un tiempo de cálculo similar. En aquella ocasión se obtuvo un beneficio de 170335, con 13 vehículos que recorrieron un total de 1229.13 unidades de distancia. Esta circunstancia sugiere que la búsqueda local de máximo gradiente empleada podría sustituirse por un algoritmo de búsqueda más agresiva, como el algoritmo del solterón.

- CONCLUSIONES
Se ha presentado una nueva heurística denominada “Big-Bang” basada en la modificación gradual de la variable espacial donde se ubican los nodos que representan los clientes. Esta estrategia de relajación consiste en reducir progresivamente, de forma escalonada, la velocidad de todos los vehículos, de forma que, al final del proceso, todos dicha velocidad sea la que corresponde con las restricciones del problema. Este procedimiento permite una fuerte tendencia hacia la reducción inicial del número de vehículos necesarios. En la ponencia se ha empleado este procedimiento para la resolución del problema VRPHESTW. Como estrategia de búsqueda local se ha empleado un esquema de búsqueda aleatoria en entornos variables, que emplea de forma probabilista un conjunto de 9 operadores y un criterio de aceptación de nuevas soluciones de máximo gradiente. En los ensayos se ha comprobado que un aumento en el factor de incremento inicial de la temperatura, del número de escalones, y de las iteraciones proporciona un incremento en la calidad de las soluciones, si bien con un mayor tiempo de cálculo. Los resultados obtenidos son de elevada calidad, si bien se sugiere el empleo de procedimientos de búsqueda local más agresivos, como por ejemplo el algoritmo del solterón, que ha dado muy buenos resultados para la resolución de este problema.
AGRADECIMIENTOS
Los autores agradecen el apoyo en este trabajo del Ministerio de Educación y Ciencia y de los fondos FEDER (Proyectos: BIA2005-03197 y REN2002-02951).
REFERENCIAS
BALL, M.O.; MAGNANTI, T.L.; MONNA, C.L.; NEMHAUSER, G.L. (Eds.) (1995). Network Routing, Handbooks in Operations Research and Management Science, vol. 8. North-Holland, Amsterdam.
GENDREAU, M.; LAPORTE, G.; MUSARAGNY, C.; TAILLARD, É.D. (1999). A tabu search heuristic for the heterogeneous fleet vehicle routing problem. Computers and Operations Research 26, pp. 1153-1173.
HOMBERGER, J.; GEHRING, H. (2005). A two-phase hybrid metaheuristic for the vehicle routing problem with time windows. European Journal of Operational Research 162, pp. 220-238.
MEDINA, J.R.; YEPES, V. (2003). Optimization of touristic distribution networks using genetic algorithms. Statistics and Operations Research Transactions 27(1), pp. 95-112.
MLADENOVIC, N.; HANSEN, P. (1997). Variable neighborhood search. Computer and Operations Research 24(11) pp. 1097-1100.
OSMAN, I.H. (1993). Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem. Annals of Operations Research 41, pp. 421-451.
POTVIN, J.Y.; ROUSSEAU, J.M. (1995). An exchange heuristic for routing problems with time windows. J. Operational Res. Soc. 46(12), pp. 1433-1446.
RUSSELL, R.A.; CHIANG, W.C. (2006). Scatter search for the vehicle routing problem with time windows. European Journal of Operations Research 169, pp.606-622.
SCHIRMPF, G.; SCHENIDER, J.; STAMM-WILBRANDT, H.; DUECK, G. (2000). Record breaking optimization results using the ruin and recreate principle. Journal of Computation Physics 159, pp. 139-171.
SOLOMON, M.M. (1987). Algorithms for the vehicle routing and scheduling problems with time window constraints. Operations Research 35(2), pp. 254-265.
TAILLARD, É.; BADEAU, P.; GENDREAU, M.; GUERTIN, F.; POTVIN, J.-Y. (1997). A tabu search heuristic for the vehicle routing problem with soft time windows. Transportation Science 31(2), pp. 170-186.
VOORNEVELD, M. (2003). Characterization of Pareto dominance. Operations Research Letters 31, pp. 7-11.
YEPES, V. (2002). Optimización heurística económica aplicada a las redes de transporte del tipo VRPTW. Tesis doctoral. Universidad Politécnica de Valencia. 352 pp.
YEPES, V.; MEDINA, J.R. (2002). Criterio económico para la optimización de rutas con flotas heterogéneas VRPHESTW, en Ibeas, A. y Díaz, J.M. (Eds.): Actas del V Congreso de Ingeniería del Transporte. Vol. 2, pp. 693-700. Santander, 11-13 junio.
YEPES, V.; MEDINA, J.R. (2004). Algoritmo del solterón aplicado a la optimización de rutas con flotas heterogéneas VPRHESTW, en Larrodé, E. y Castejón, L. (Eds.): Actas del VI Congreso de Ingeniería del Transporte. Vol. 2, pp. 759-766. Zaragoza, 23-25 de junio.
YEPES, V.; MEDINA, J.R. (2006). Economic heuristic optimization for heterogeneous fleet VRPHESTW. Journal of Transportation Engineering, ASCE 132(4), pp. 303-311.
