holgura – El blog de Víctor Yepes

En un artículo anterior ya vimos los errores que suelen cometerse en el cálculo de las holguras, especialmente cuando se está trabajando con un diagrama de precedencias. El concepto de holgura se emplea en la planificación para describir la libertad de desplazamiento que, dentro de un cierto intervalo de tiempo, puede tener un suceso o una actividad. También suelen llamarse juegos o tiempos flotantes. En esta entrada vamos a interpretar qué significa cada una de las holguras que existen en una actividad. Esta interpretación es fundamental para el responsable de la tarea, pues debe comprender qué implica el retraso de su actividad en el contexto del proyecto o de la obra que está realizando.

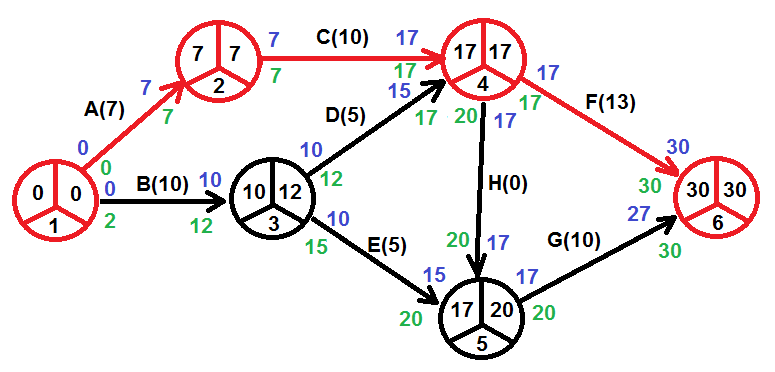
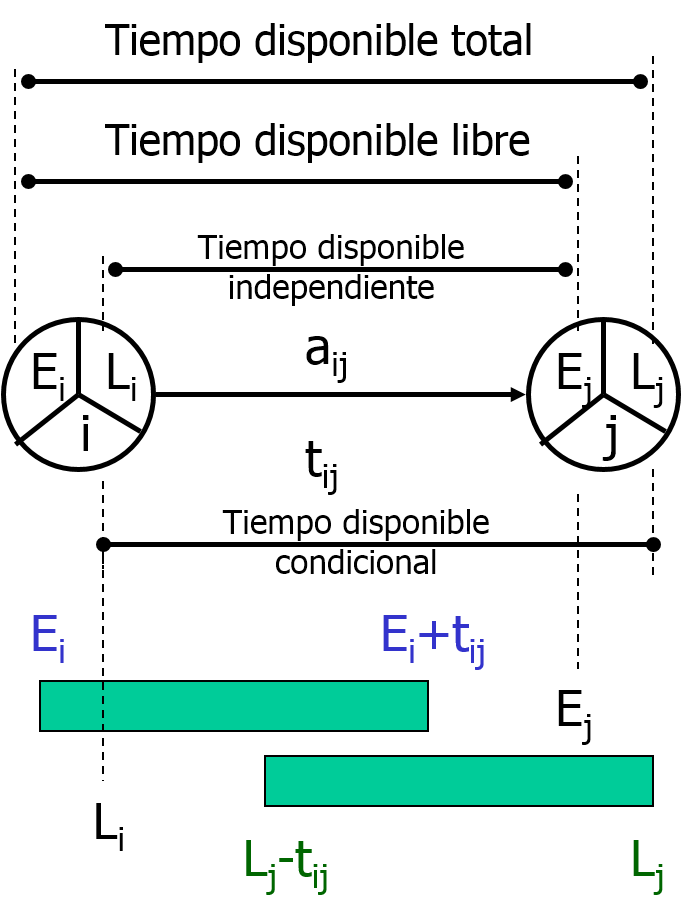
En la Figura 1 se muestra cómo una actividad a_ij se representa como una flecha orientada desde parte del nodo i y llega al nodo j. A los nodos se les denomina “sucesos” o “acontecimientos“.

Figura 1. Definición de los tiempos disponibles de una actividad

Estos nodos presentan una holgura de suceso o margen de etapa que, en el caso del nodo i, se calcula de la siguiente forma:

En esta expresión, E_irepresenta la fecha más temprana del acontecimiento i, mientras que L_irepresenta la fecha más tardía.

Con los conceptos anteriores, es fácil demostrar que el margen de etapa en un determinado nudo es igual a la diferencia entre los tiempos “disponible total” y “disponible libre” de cualquier actividad que termine en dicho nudo. En efecto, para una actividad a_ij, se tiene:

Pues bien, cualquier actividad, como la a_ij, debe transcurrir entre sus nodos de inicio y de final. Como cada nodo presenta dos fechas, una más temprana y otra más tardía, los nodos de entrada y salida de una actividad dan lugar a cuatro fechas que definen cuatro posibles tiempos disponibles para la actividad (ver Figura 1).

Se define como holgura o margen de una actividad como el tiempo disponible que queda después de descontar la duración de dicha tarea. Como existen cuatro posibles tiempos disponibles, se podrán definir cuatro tipos de holguras para las actividades. Es evidente que si una actividad pertenece a un camino crítico, no tiene holguras.

Recordemos que la fecha más tardía para que la actividad a_ij pueda empezar, se calcula como L_j – t_ij. Esta fecha no tiene por qué coincidir con L_i, tal y como ya discutimos en un artículo anterior.

Si dibujamos la actividad a_ij en un diagrama de barras, podríamos representar la actividad empezando lo antes posible, es decir, en el instante E_i. Otra opción sería dibujar la actividad empezando en el instante más tardío del acontecimiento i (volvemos a recordar que no es la fecha más tardía en que puede empezar la actividad a_ij). De esta forma, podemos visualizar las holguras que presenta la actividad en la Figura 2. Se puede ver una quinta holgura, que es la holgura interferente, como diferencia entre la holgura total y la holgura libre.

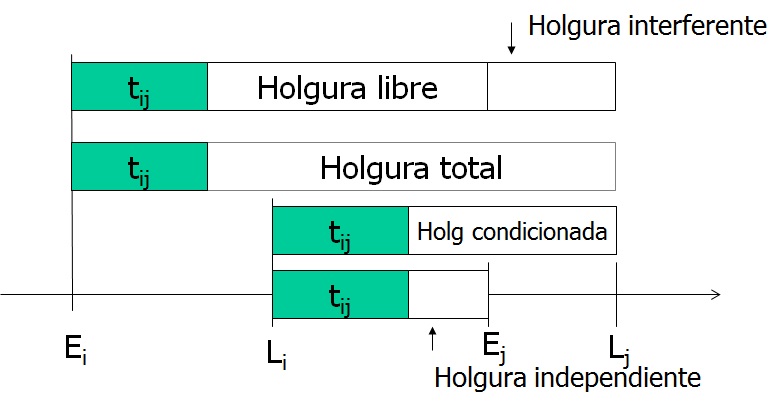
Figura 2. Representación de las holguras de una actividad

Vamos a analizar cada una de estas holguras para poder interpretar lo que significan. Ya os adelanto que las holguras más empleadas son la total y la libre. Pero hay más.

Holgura total

La holgura total se define como la diferencia entre el tiempo disponible total y la duración de la actividad. Es una holgura que es mayor o igual a cero y se calcula de la siguiente forma:

Es el margen en que una actividad puede atrasar su inicio más temprano, su término más temprano o su duración, sin atrasar el término programado del proyecto. Si se consume esta holgura, la actividad y el suceso siguiente se hacen críticos. Este es el valor menos probable de todas las holguras, pues está condicionado al hecho de que la actividad comience en el tiempo más optimista y que la actividad no sufra desviación alguna.

La holgura total pertenece al camino del que forma parte la actividad. Es decir, que dicha holgura se puede consumir completamente en una de las tareas del camino o distribuir el margen entre distintas actividades de dicho camino. Es por ello que a la holgura total también suele llamarse “margen de camino“.

Holgura libre

La holgura libre se define como la diferencia entre el tiempo disponible libre y la duración de la actividad, siendo un valor mayor o igual a cero. Se calcula de la siguiente forma:

Se trata de la cantidad de tiempo en que una actividad puede atrasar su inicio más temprano, su término más temprano o aumentar su duración, sin atrasar el inicio más temprano de sus actividades subsecuentes. Esta holgura es muy importante para el gestor de la actividad, pues si mantengo el retraso dentro de este límite, no afectaré a las actividades que vengan después. Si se consume esta holgura, la red permanece inalterada. Por eso se llama a esta holgura “margen de actividad“.

La holgura total se puede obtener sumando a la holgura libre el margen de la etapa de llegada. En efecto,

Como se puede comprobar, la holgura libre no puede ser mayor a la holgura total. Además, la condición necesaria (pero no suficiente) para que exista es que llegue más de una actividad al nodo de terminación de la actividad que estamos analizando.

Holgura interferente

La holgura interferente se define como la diferencia entre la holgura total y la holgura libre. Se interpreta como la cantidad de tiempo que se puede demorar la terminación de una actividad, sin demorar la terminación del proyecto, pero cuyo uso retrasará el inicio de alguna de las actividades siguientes. La holgura interferente es exactamente el margen de etapa del nodo de llegada de la actividad. Se puede calcular de la siguiente forma:

Cuando se representa en un diagrama de barras una actividad, empezando lo antes posible, si existe holgura total, debe diferenciarse con un trazo vertical qué parte es holgura libre y qué parte es interferente. En la Figura 3 se muestra cómo debe hacerse.

Figura 3. Representación de la holgura total, libre e interferente en un diagrama de barras

Holgura independiente

La holgura independiente es la diferencia entre el tiempo disponible independiente y la duración de la actividad. También se llama “holgura mínima“. Suele ser un valor muy pequeño, incluso negativo. Además, siempre es menor o igual a la holgura libre (Figura 2). Se calcula de la siguiente forma:

Esta holgura es el retraso que puede sufrir una actividad con su inicio demorado al máximo por las actividades precedentes, sin que ese retraso ocasione aplazamientos en el comienzo de cualquier actividad posterior. Al igual que la holgura libre, la independiente no se comparte con ninguna otra actividad.

En la práctica no se suele emplear esta holgura, aunque puede ser útil como parámetro representativo de las condiciones más desfavorables en que puede desarrollarse una actividad.

La holgura independiente se puede calcular como la holgura total menos la suma de los márgenes de las etapas inicial y final de la actividad. También como la diferencia entre la holgura libre y el margen de la etapa inicial de la actividad. Por dicho motivo, la holgura independiente no puede superar a la holgura libre, al igual que la holgura libre no podía ser mayor a la holgura total.

Holgura condicionada

La holgura condicionada, también llamada “holgura intermedia“, es el margen en que una actividad puede atrasar su inicio demorado al máximo por las actividades precedentes, su término más temprano o su duración, sin atrasar el término programado del proyecto. Se puede calcular de la siguiente forma:

Como se puede observar, su interpretación es similar a la holgura total, pero suponiendo que el inicio se ha retrasado al máximo posible por las actividades precedentes.

Si observamos la Figura 2, es fácil deducir que la holgura condicionada es la suma de la holgura independiente y la interferente. O lo que es lo mismo, la holgura condicionada es la holgura independiente, menos la diferencia de la holgura total y la libre.

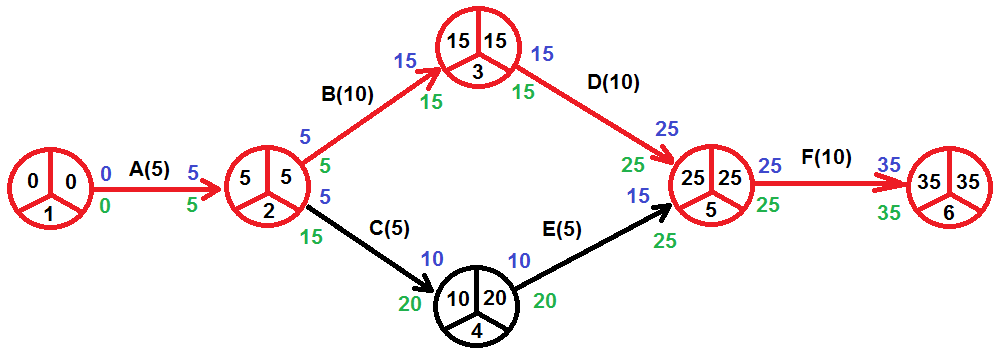
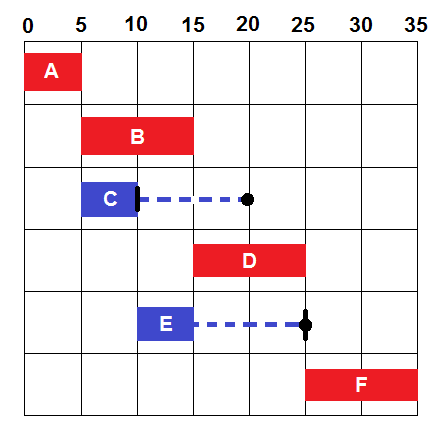
A modo de ejemplo, vamos a analizar las holguras de la actividad E perteneciente al siguiente proyecto:

Como se puede observar, la actividad E podría empezar, como muy pronto, en la etapa 10, y como muy tarde, en la etapa 15. Asimismo, podría terminar, como muy pronto, en la etapa 15, y como muy tarde, en la etapa 20.

El cálculo de las holguras sería el siguiente:

Holgura total: L5 – E3 – t35 = 20 – 10 – 5 = 5

Holgura libre: E5 – E3 – t35 = 17 – 10 – 5 = 2

Holgura interferente: L5 – E5 = 20 – 17 = 3

Holgura independiente: E5 – L3 – t35 = 17 – 12 – 5 = 0

Holgura condicionada: L5 – L2 – t35 = 20 – 12 – 5 = 3

Referencias:

YEPES, V.; MARTÍ, J.V.; GONZÁLEZ-VIDOSA, F.; ALCALÁ, J. (2012). Técnicas de planificación y control de obras. Editorial de la Universitat Politècnica de València. Ref. 189. Valencia, 94 pp. Depósito Legal: V-423-2012.

YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Las técnicas de programación de proyectos basadas en el cálculo de redes se explican normalmente en los grados de ingeniería civil. Los estudiantes automatizan el cálculo de estas redes de forma sencilla, tanto en el caso de las redes de flechas como en el de las redes de precedencias. Sin embargo, muchas veces no comprenden o les resulta confuso la idea de holgura de un suceso o de una actividad. Incluso en algunos libros de texto confunden los conceptos. Quiero en este artículo aclarar mediante un ejemplo dónde están los problemas asociados al cálculo de las holguras.

Por cierto, podéis repasar en cálculo de una red de flechas o una red de precedencias en alguno de los artículos y vídeos que grabé en su momento. Basta que pulséis el enlace correspondiente.

Sea un proyecto compuesto por seis actividades cuyas relaciones de precedencia y duración se muestran en la Tabla 1. En dicha tabla, una actividad situada en una línea precede a la actividad de una columna si la casilla se encuentra marcada. Así, por ejemplo, la actividad A precede tanto a la actividad B como a la C. Para simplificar, las relaciones son final-principio, es decir, la actividad subsecuente no puede iniciarse hasta que se hayan terminado las actividades que le preceden.

Tabla 1. Relación de precedencias entre las actividades.

Es fácil representar y calcular el diagrama de flechas correspondiente. Este proyecto tiene un plazo de 35 etapas, siendo el camino crítico el representado por las actividades A, B, D y F (ver Figura 2).

Figura 2. Representación y cálculo del diagrama de flechas

Este mismo proyecto se podría haber calculado usando un diagrama de precedencias, cuya resolución puede verse en la Figura 3. Observe que las fechas más tempranas de inicio de cada actividad tienen un color azul, mientras que las más tardías están en verde. Estas fechas se pueden ver también en la Figura 2.

Figura 3. Representación y cálculo del diagrama de precedencias

Si representamos el proyecto en un diagrama de barras, se obtiene la Figura 4. Se observa que en este diagrama se ha representado el inicio de cada actividad lo antes posible. Además, se han dibujado la holgura total y libre, separadas ambas por una línea vertical. La actividad C no tiene holgura libre, mientras que en la actividad E, la holgura total y libre coinciden.

Figura 4. Diagrama de barras o de Gantt, con las actividades empezando lo antes posible

Pues veamos ahora dónde están los problemas con las holguras. Previamente, vamos a definir la holgura de una actividad como la diferencia entre el tiempo disponible para realizarla y su duración.

Las holguras se definen en función de los nodos de entrada y salida de la actividad, según se representa en la Figura 5. Existen cinco tipos de holgura: total, libre, independiente, condicional e interferente. Esta última es la diferencia entre la holgura total y la holgura libre.

Figura 5. Definición de los tiempos disponibles de una actividad

El primer error conceptual que se comete es definir las fechas de los nodos de entrada y salida de una actividad como las fechas más tempranas y tardías de inicio o terminación de dicha actividad. Solo Ei y Lj son la fecha más temprana de inicio y la más tardía de finalización de la actividad. Las fechas Li y Ej corresponden a los nodos correspondientes. En efecto, la fecha más tardía de inicio sería Lj -tij; mientras que la fecha más temprana de terminación sería Ei+tij. Se pueden ver ambas fechas en las barras verdes de la Figura 5. Únicamente en el caso de las fechas representadas dentro de la caja de la actividad de un diagrama de precedencias, tenemos las fechas más tempranas y tardías de inicio y terminación de la actividad correspondiente (Figura 6).

Figura 6. Notación y forma de representación de una actividad en un diagrama de precedencias

El segundo error conceptual está en algunos libros cuando dicen lo siguiente “El concepto y cálculo de las holguras usando el diagrama de precedencias en nada difiere del introducido para el diagrama de flechas“. En sí misma, esta frase es correcta. El error viene cuando se confunde el comienzo más tardío de la actividad con Li y el final más temprano de la actividad con Ej.

Es por todo lo anterior que, en el caso del cálculo de la holgura total, no hay ningún problema en su cálculo con el diagrama de flechas o de precedencias. Pero el resto de holguras puede ser erróneo si utilizamos un diagrama de precedencias. Veamos qué ocurre con la actividad C de este proyecto.

Holgura total: L4 – E2 – t24 = 20 – 5 – 5 = 10

Holgura libre: E4 – E2 – t24 = 10 – 5 -5 = 0

Holgura independiente: E4 – L2 – t24 = 10 – 5 – 5 = 0

Holgura condicionada: L4 – L2 – t24 = 20 – 5 – 5 = 10

Fíjese que el comienzo más tardío de la actividad C sería 15, que es un valor diferente a L2 = 5. En este caso, la terminación más temprana de la actividad C sería 10, que coincide en este caso con E4 = 10.

Conclusión: Si se usa el diagrama de precedencias, hay que tener mucho cuidado en calcular holguras de una actividad, excepto para el caso de la holgura total. En el diagrama de flechas no existe ningún problema. No confundir las fechas de comienzo más tardío y final más temprano de una actividad con los correspondientes a los nodos de entrada y salida de dicha actividad.