En el procesamiento de áridos se necesita energía para reducir el tamaño del material que entra en una máquina de fragmentación. El cálculo de la energía necesaria resulta de interés, no solo desde el punto de vista teórico, sino también para estimar el coste de la energía en la operación.
Cuando se aplica una fuerza para romper una partícula, al principio se deforma y se almacena la energía aplicada en el material. Pero si la fuerza sobrepasa el límite de resistencia, la partícula se rompe consumiendo cierta energía, transformándose la sobrante en calor, ruido y energía cinética, entre otras.
Existen distintas leyes que proporcionan la energía necesaria para una operación de fragmentación determinada. La Ley de Rittinger es adecuada para partículas finas, de diámetro inferior a 74 μm, y dice que el área de la nueva superficie producida por el nuevo machaqueo o molienda es directamente proporcional al trabajo útil consumido. La Ley de Kick se aplica a partículas gruesas, de diámetro mayor a 10 cm, y dice que el trabajo requerido es directamente proporcional a la reducción de volumen entre las partículas antes y después de la operación de fragmentación o molienda.
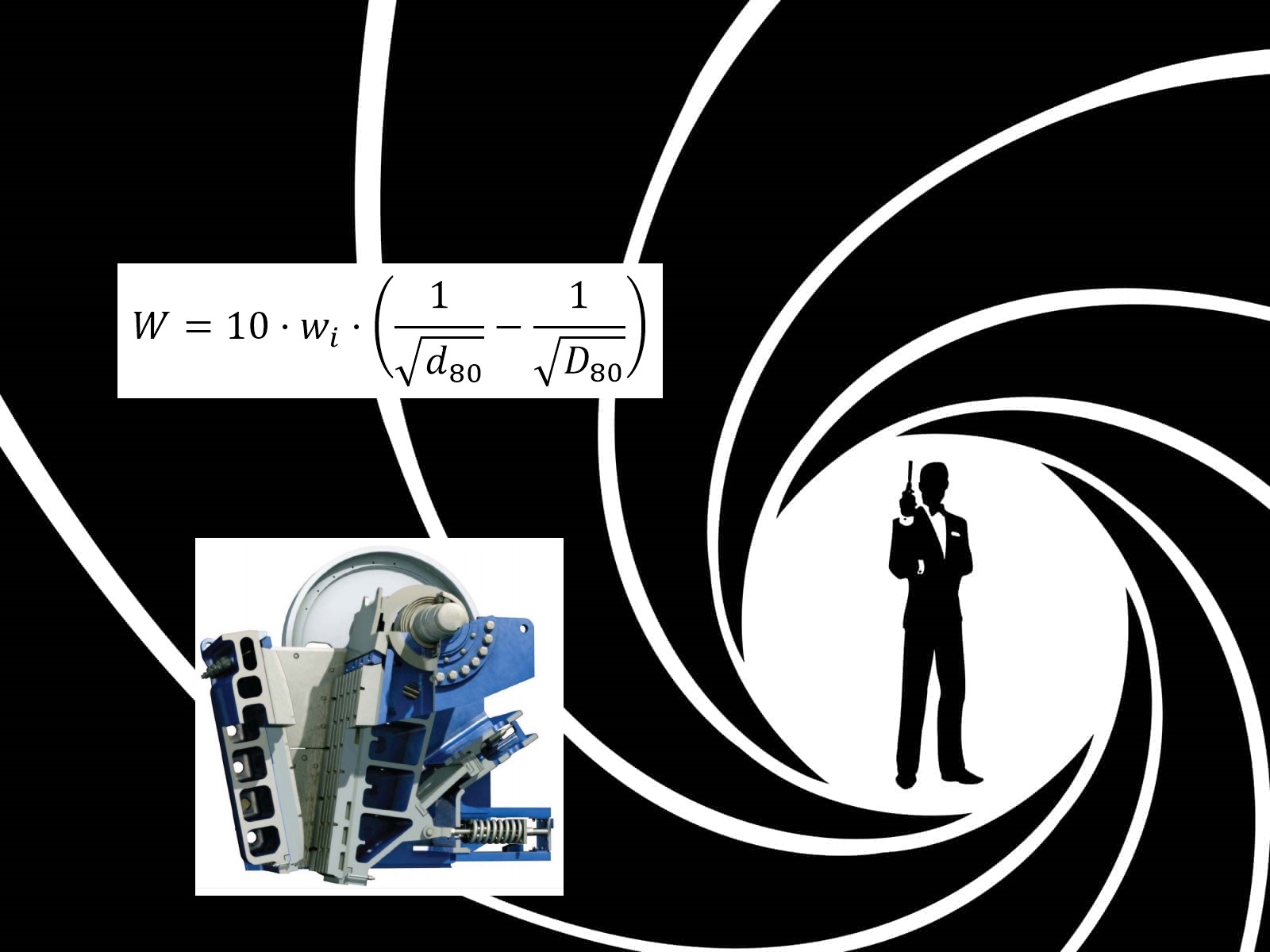
Sin embargo, F. C. Bond (1951), a partir del estudio de un gran número de instalaciones, dedujo su Ley de Bond, que dice que el trabajo consumido es proporcional a la nueva longitud de fisura producida por la rotura de las partículas, pues una vez creada la fisura, la roca parte. Esta ley cubre el vacío de las otras dos leyes anteriores, para diámetros superiores a 74 μm y menores a 10 cm.
Para que se pueda entender esta ley y otros conceptos como el de razón de reducción o el de curva granulométrica, os dejo un problema resuelto y varios vídeos que espero os sea de interés.
Referencias:
FUEYO, L. (1999). Equipos de trituración, molienda y clasificación: tecnología, diseño y aplicación. Editorial Rocas y Minerales. 1ª edición. Fueyo Editores. Madrid, 371 pp. ISBN: 84-923128-2-3.
LÓPEZ JIMENO, C. (ed.) (1998). Manual de áridos. Prospección, explotación y aplicaciones. E.T.S. de Ingenieros de Minas de Madrid, 607 pp.
MARTÍ, J.V.; GONZÁLEZ, F.; YEPES, V. (2005). Temas de procedimientos de construcción. Extracción y tratamiento de áridos. Editorial de la Universidad Politécnica de Valencia. Ref. 2005.165. Valencia.
MARTÍNEZ PAGÁN, P. (2021). Ejercicios resueltos de plantas de tratamiento de recursos minerales. Universidad Politécnica de Cartagena, CRAI Biblioteca, Cartagena, 211 pp.
TIKTIN, J. (1994). Procesamiento de áridos: instalaciones y puesta en obra de hormigón. Universidad Politécnica de Madrid. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Madrid, 360 pp. ISBN: 84-7493-205-X.
YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
