La naturaleza siempre ha servido de inspiración para arquitectos, ingenieros y diseñadores. La tecnología informática ha facilitado las herramientas para analizar y simular la complejidad observada en la naturaleza y aplicarla a formas estructurales de construcción y los mecanismos de organización urbana. Entre ellas destacamos la geometría fractal y el diagrama de Voronoi.
La geometría fractal no ha dejado de evolucionar desde las investigaciones del matemático polaco nacionalizado francés y estadounidense, Benoît Mandelbrot en los años 70 del siglo pasado. Un fractal es un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas. Lo interesante es que la forma de los fractales parecen describir la Naturaleza y encuentra su geometría una gran variedad de aplicaciones en urbanismo, arquitectura, computación o ingeniería estructural (Figura 1).
El diagrama de Voronoi (nombre que se debe al matemático ruso Gueorgui Voronói) se crea al unir los puntos entre sí, trazando las mediatrices de los segmentos de unión (Figura 2). Las intersecciones de estas mediatrices determinan una serie de polígonos en un espacio bidimensional alrededor de un conjunto de puntos de control, de manera que el perímetro de los polígonos generados sea equidistante a los puntos vecinos y designan su área de influencia.

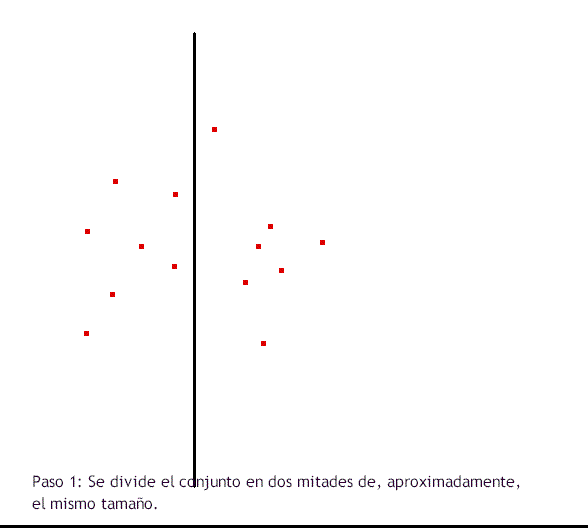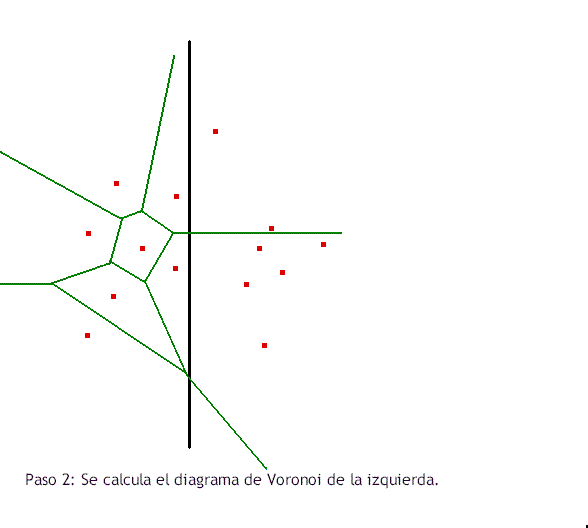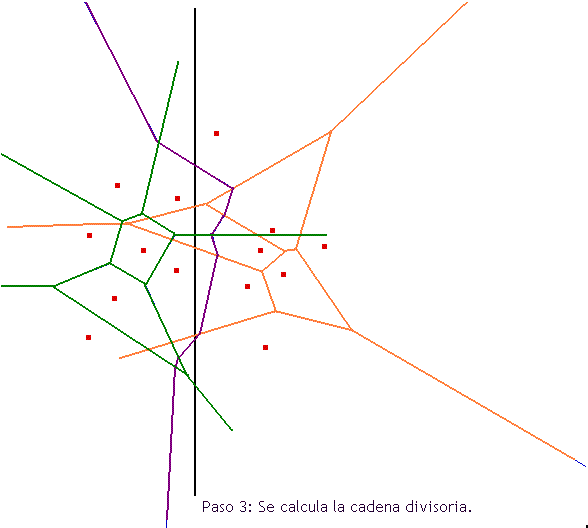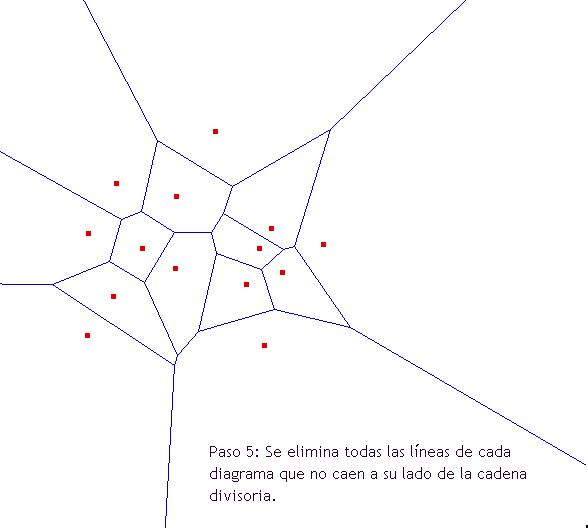
Hasta mediados de los ochenta, la mayoría de las implementaciones para computar el diagrama de Voronoi usaban el algoritmo incremental cuadrático, admitiendo su mayor lentitud para evitar la complejidad del código divide y vencerás (Figura 3). En 1985 Fortune inventó un inteligente algoritmo de barrido plano que resulta tan simple como el incremental, pero en tiempo O(n log n). Para los más curiosos, podéis utilizar MATLAB para realizar ejemplos sobre los diagramas de Voronoi utilizando la funciónvoronoin. El enlace lo tenéis aquí: https://es.mathworks.com/help/matlab/math/voronoi-diagrams.html
La profesora de la Universidad de Sevilla, Clara Grima, nos describe en un artículo de divulgación, «El diagrama de Voronoi, la forma matemática de dividir el mundo«, algunas aplicaciones del diagrama de Voronoi, que van desde la distribución de farmacias en una ciudad, a el mapa del cólera de John Snow o a la ventaja posicional de un equipo de fútbol.
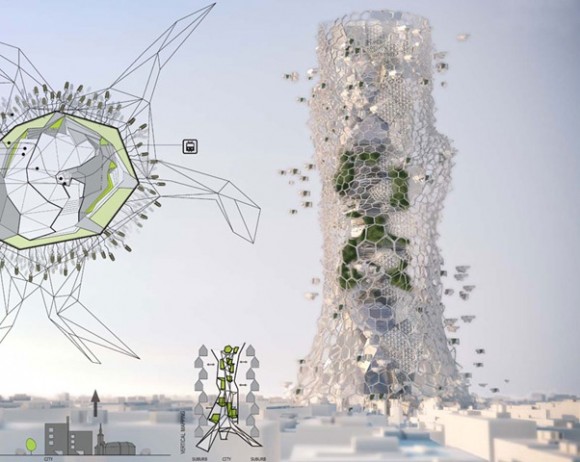
Pero aquí lo interesante es saber que, basándose en este diagrama, se pueden diseñar estructuras y espacios urbanos de gran interés. En la Figura 4 podemos ver la oficina central de Alibaba. Este tipo de estructuras resultan agradables, estáticamente eficientes y adecuadas para trabajar como un sistema estructural espacial. Además, la estructura se puede modelar por un conjunto de puntos y admite el diseño paramétrico. Se denomina diseño paramétrico a un proceso de diseño basado en un esquema algorítmico que permite expresar parámetros y reglas que definen, codifican y aclaran la relación entre los requerimientos del diseño y el diseño resultante.

En la Figura 5 se observa la posibilidad de estos diagramas en el caso de pantallas arquitectónicas. Como vemos, las posibilidades estructurales son de un gran interés.

Aquí tenemos una explicación de los diagramas de Voronoi. También el vídeo explica cómo construir a partir de una serie de puntos generadores los famosos Polígonos de Thiessen que conforman el diagrama antes mencionado.
En el presente vídeo se explican los fractales.
Os dejo también un artículo sobre el diagrama de Voronoi como herramienta de diseño, de María Loreto Flores. Espero que os sea de interés
