En este post voy a enseñaros una herramienta muy interesante desde el punto de vista docente. Se trata de los Laboratorios Virtuales. Los alumnos pueden interactuar en línea para aprender. En este caso os paso uno desarrollado por los profesores de la Unidad Docente de Caminos y Aeropuertos de la Universitat Politècnica de València, los profesores Francisco Javier Camacho Torregrosa, Ana María Pérez Zuriaga y Alfredo García García.
En este laboratorio se aborda el diseño de la transición del peralte entre curvas en planta de diferente sentido de giro. Existen dos posibles formas de realizar la transición del peralte, en función de la longitud de la recta intermedia. En caso de que la recta intermedia sea suficientemente larga, se dispondrá bombeo en la misma, para lo cual se realizará la transición del peralte y del desvanecimiento del bombeo propio de las curvas aisladas. En el caso de que la longitud de la recta intermedia sea insuficiente (menor de 150 m en carreteras del grupo 2 y 300 m en carreteras del grupo 1), la transición del peralte se realizará por medio de la comúnmente llamada ‘pajarita’, que impone un cambio rápido de peralte en la zona central, no existiendo bombeo en dicha recta. En el tramo circular de las curvas en planta se mantendrá el peralte constante en todo momento. Los objetivos de este laboratorio virtual son: Identificar la influencia de los diferentes parámetros que forman parte del diseño de acuerdos de carreteras. Y representar el perfil longitudinal de una carretera a la escala adecuada (10H:1V).
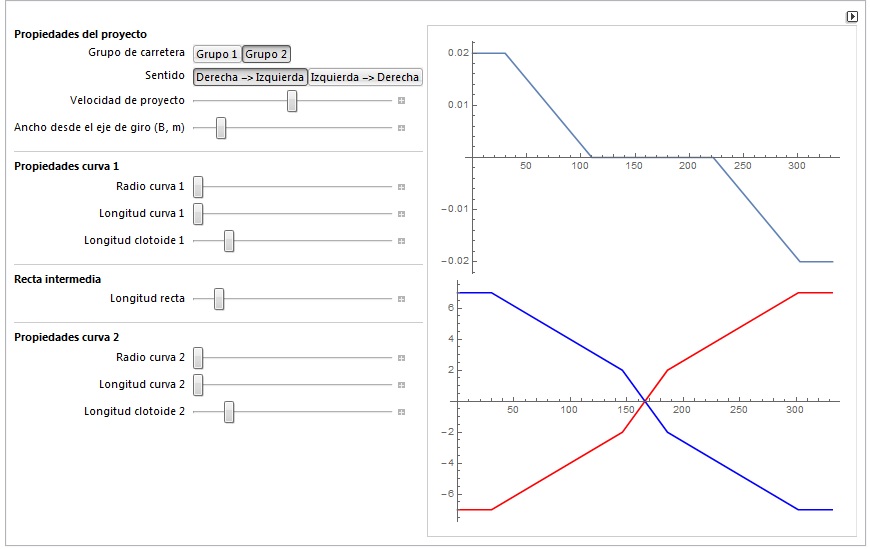
Las instrucciones de este laboratorio son las siguientes: ‘Propiedades del proyecto’ permite controlar las características de la carretera a la que pertenece la curva en ‘S’: su grupo, el sentido de las curvas, la velocidad del proyecto y la distancia desde el eje de giro a los bordes de calzada. ‘Propiedades curva 1’ y ‘Propiedades curva 2’ permiten controlar las características de cada una de las curvas que se van a diseñar. A partir de sus radios se obtendrá un valor del peralte, representado en el diagrama. Las longitudes de las clotoides y de las curvas también son controlables desde la aplicación. ‘Recta intermedia’ controla la longitud de dicha recta, o su eliminación (en el caso de longitud nula).
El enlace al laboratorio virtual es el siguiente: http://mathematica.upvnet.upv.es/eslabon/Ejercicio.asp?do=Peralte
NOTA: Para poder ver los laboratorios necesita el plugin del Wolfram CDF Player. Si no lo tiene instalado en su equipo, puede descargarlo en la página web de Wolfram. Si utiliza un equipo público o no disponde de privilegios para instalar software, puede visualizar el laboratorio desde un servidor remoto. Tan sólo necesitará que su navegador incluya soporte para aplicaciones Java. Pulse aquí para visualizar el laboratorio sin instalar el plugin de Mathematica CDF Player
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.