La planificación y gestión de redes de distribución de baja demanda exige disponer de técnicas eficientes de optimización de rutas. El sistema de optimización de rutas disponible, no sólo afecta el desarrollo de operaciones sino, también las decisiones tácticas y estratégicas como el tamaño óptimo de flota, estimación de costes, políticas de publicidad y rotura de servicio, etc. Por ejemplo, es habitual la venta de paquetes turísticos que incluyen el transporte; los precios se fijan mucho antes de que la demanda de transporte sea conocida, siendo frecuentes las cancelaciones de última hora y la llegada de nuevos clientes. Si el número de pasajeros que debe ser transportado es pequeño, en comparación con la máxima capacidad de carga del vehículo óptimo a la distancia correspondiente, los beneficios o pérdidas generadas por el transporte dependen críticamente de la eficiencia del sistema de optimización de rutas. La Figura describe la influencia de la optimización de operaciones en la planificación y gestión de redes de distribución de baja demanda.
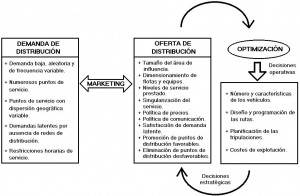
Así pues, la planificación y gestión de redes de distribución de baja demanda genera una variedad de problemas de decisión que dependen críticamente de la optimización de operaciones, con espacios de soluciones muy grandes y además crecientes exponencialmente con el número de destinos y tamaño de flota. Esta explosión combinatoria de soluciones y la complejidad de las variables a optimizar impiden que la optimización pueda ser abordada con técnicas de optimización exactas; por el contrario, las técnicas meta-heurísticas y probabilísticas son alternativas siempre viables que, aunque no garantizan alcanzar la solución óptima absoluta, sí pueden proporcionar buenas soluciones a problemas reales complejos (ver Diaz et al., 1996). En este contexto, los sistemas inteligentes son métodos apropiados para resolver problemas complejos de optimización combinatoria como el planteado (ver Goonatilake and Treleaven, 1996, Fayyard et al., 1996 y Medina, 1998). En este artículo, se ha utilizado un algoritmo genético originalmente diseñado para resolver el TSP, para abordar problemas más complejos como el CVRP y el SCVRP, utilizando funciones de coste y restricciones muy variadas.
Por otro lado, el problema de optimización de operaciones de transporte es crucial para la propia existencia de un cierto nicho de mercado de baja demanda. Si se consigue una distribución muy eficiente, es posible aflorar una demanda latente y satisfacerla con una flota pequeña y un costo razonable. Esta situación se produce en el mercado turístico con destinos poco masificados. En un ejemplo de aplicación presentado por Medina y Yepes (2003), se utiliza un aeropuerto hub, donde tanto para fijar precios como para definir la mejor estrategia comercial, resulta imprescindible disponer de un sistema flexible para optimizar la distribución de pasajeros y unos modelos estocásticos de simulación de escenarios.
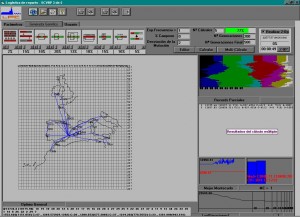
Referencias:
DIAZ, A., GLOVER, F., GHAZIRI, H.M., GONZÁLEZ, J.L., LAGUNA, M., MOSCATO, P. y TSENG, F.T.(1996). Optimización Heurística y Redes Neuronales en Dirección de Operaciones e Ingeniería. Editorial Paraninfo S.A., Madrid (España).
FAYYARD, U.M., PIATETSKI-SHAPIRO, G., SMYTH, P. y UTHURUSAMI, R.(1996). Advances in Knowledge Discovery and Data Mining. MIT Press.
GOONATILAKE, S. and TRELEAVEN, P. (1996). Intelligent Systems for Finance and Business. John Wiley.
MEDINA, J.R.(1998). Algoritmos genéticos para la optimización de redes de distribución. Actas del X Congreso Panamericano de Ingeniería de Tránsito y Transporte. Santander 1998, Ministerio de Fomento (España), pp. 339-347.
MEDINA, J.R.; YEPES, V. (2003). Optimization of touristic distribution networks using genetic algorithms. Statistics and Operations Research Transactions, 27(1): 95-112. ISSN: 1696-2281. (pdf)
