En el corazón de nuestra civilización digital late un motor invisible que solemos dar por sentado. Lo que en el siglo IX nació como una serie de reglas rígidas para el cálculo algebraico —el legado de Al-Juarismi— ha evolucionado hasta convertirse en el concepto moderno de algoritmo: una sofisticada «receta» diseñada para manipular información mediante operaciones elementales. En la actualidad, los algoritmos no son solo curiosidades matemáticas, sino la infraestructura lógica que decide desde la ruta de un camión de reparto hasta la resistencia de un viaducto de hormigón. Sin embargo, ¿comprendemos realmente las leyes que rigen su eficiencia o somos ciegos ante las reglas que separan lo posible de lo imposible?
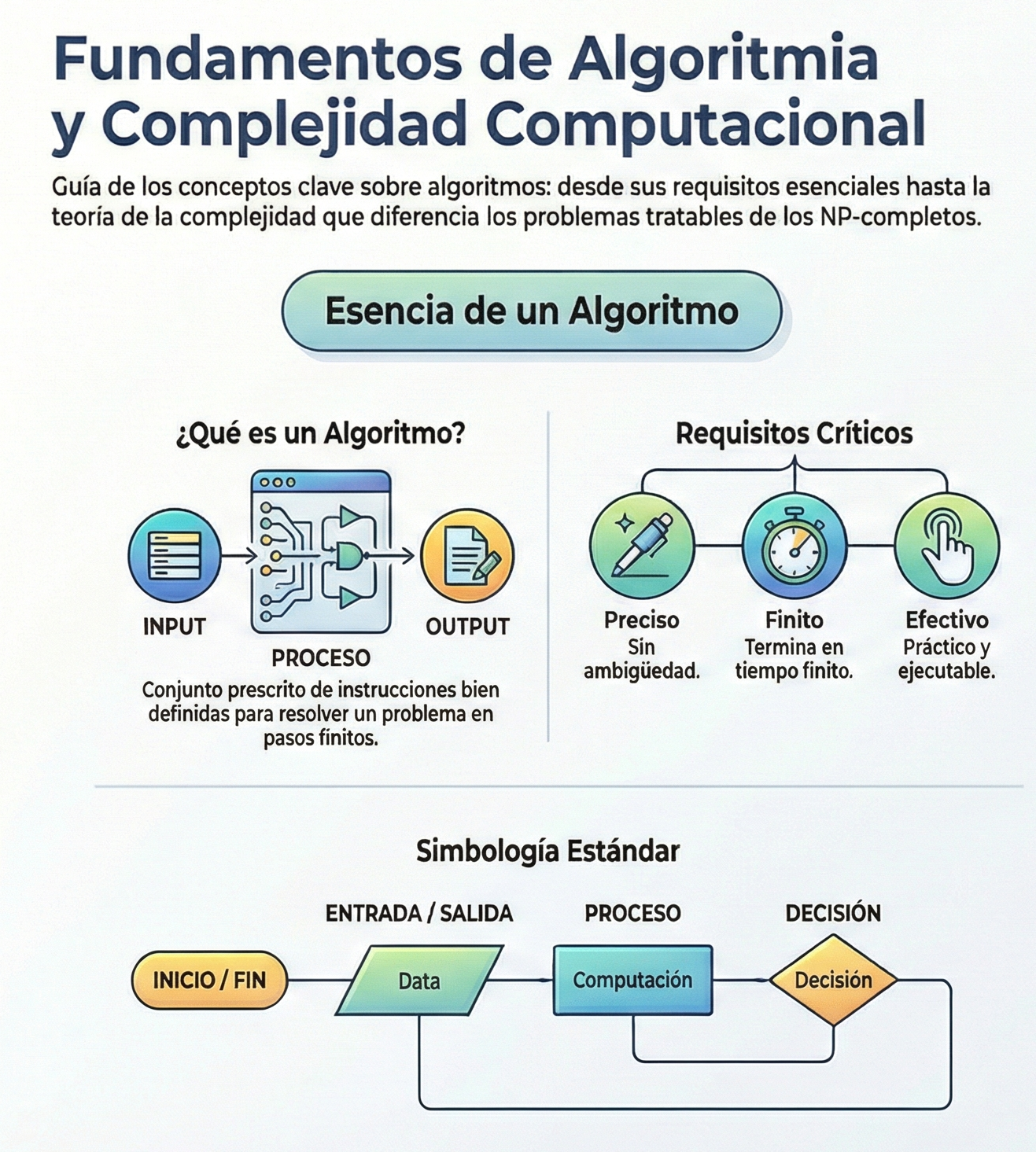
El concepto de algoritmo ha evolucionado desde una acepción antigua, centrada en reglas para operaciones algebraicas, hacia una visión moderna: un conjunto prescrito de reglas o instrucciones bien definidas para resolver un problema específico en un número finito de pasos. En esencia, se trata de un método para manipular información mediante operaciones elementales.
A continuación, desvelamos cinco realidades esenciales para navegar por este universo de precisión y complejidad.
1. Los pilares del rigor: más allá del simple «paso a paso».
A menudo se define el algoritmo como una lista de instrucciones, pero para la ciencia de la computación esta definición es insuficiente. Un algoritmo debe ser un baluarte contra la ambigüedad, ese «fantasma en la máquina» que detiene en seco cualquier proceso lógico. Un método solo alcanza la categoría de algoritmo si cumple cuatro condiciones necesarias, pero no suficientes.
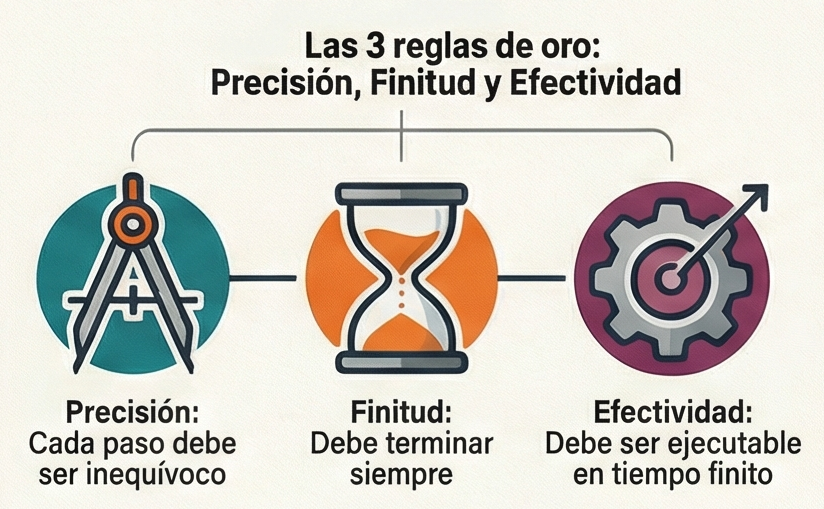
- Precisión: cada instrucción debe indicar exactamente qué acción realizar, sin margen de interpretación.
- Finitud: el proceso debe tener un final garantizado tras un número determinado de pasos.
- Efectividad: cada operación debe poder ser ejecutada por el ejecutor (humano o máquina) en un tiempo finito.
- Entrada y salida: debe existir un punto de partida de datos y un resultado concreto.
La finitud no es solo una exigencia teórica, sino también una restricción física. En un mundo de recursos limitados, un proceso que no termina nunca no es una solución, sino un abismo de consumo de energía.
2. El enigma de P vs. NP
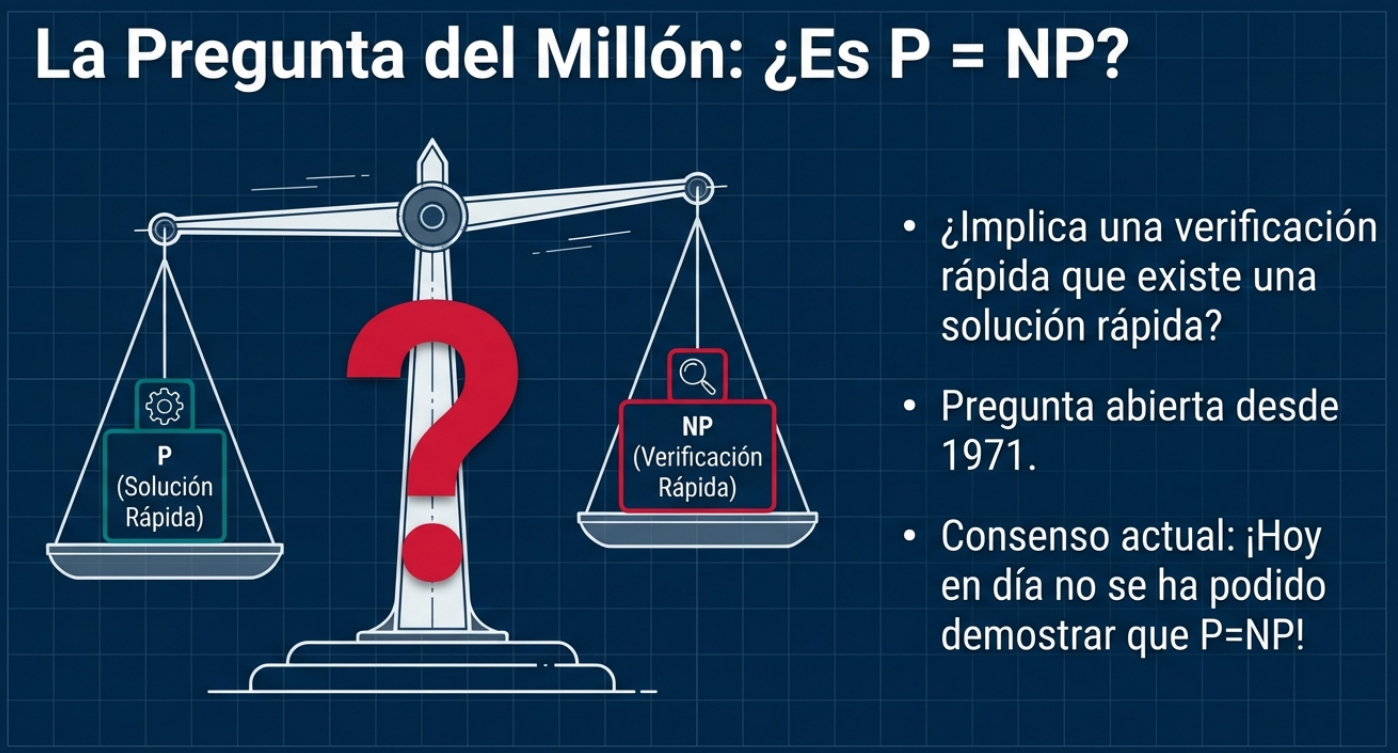
Existe una frontera que divide los problemas en dos grandes categorías. Por un lado, la clase P, que agrupa los problemas que podemos resolver rápidamente (de forma eficiente). Por otro lado, está la clase NP, que incluye problemas cuya solución, aunque difícil de encontrar, puede verificarse con rapidez una vez que la tenemos. La gran pregunta que obsesiona a los genios desde 1971 es si resolver es intrínsecamente más difícil que verificar.
«¡Hoy en día no se ha podido demostrar que P = NP!»
Científicamente, sabemos que P ⊂ NP, pero el gran misterio radica en el «empate». Si se demostrara que P = NP, significaría que para la mayoría de los retos complejos de nuestra era —desde la criptografía hasta el diseño estructural— existen algoritmos de una eficiencia asombrosa que aún no hemos logrado ver.
3. La tiranía del tiempo: el análisis del «peor caso».
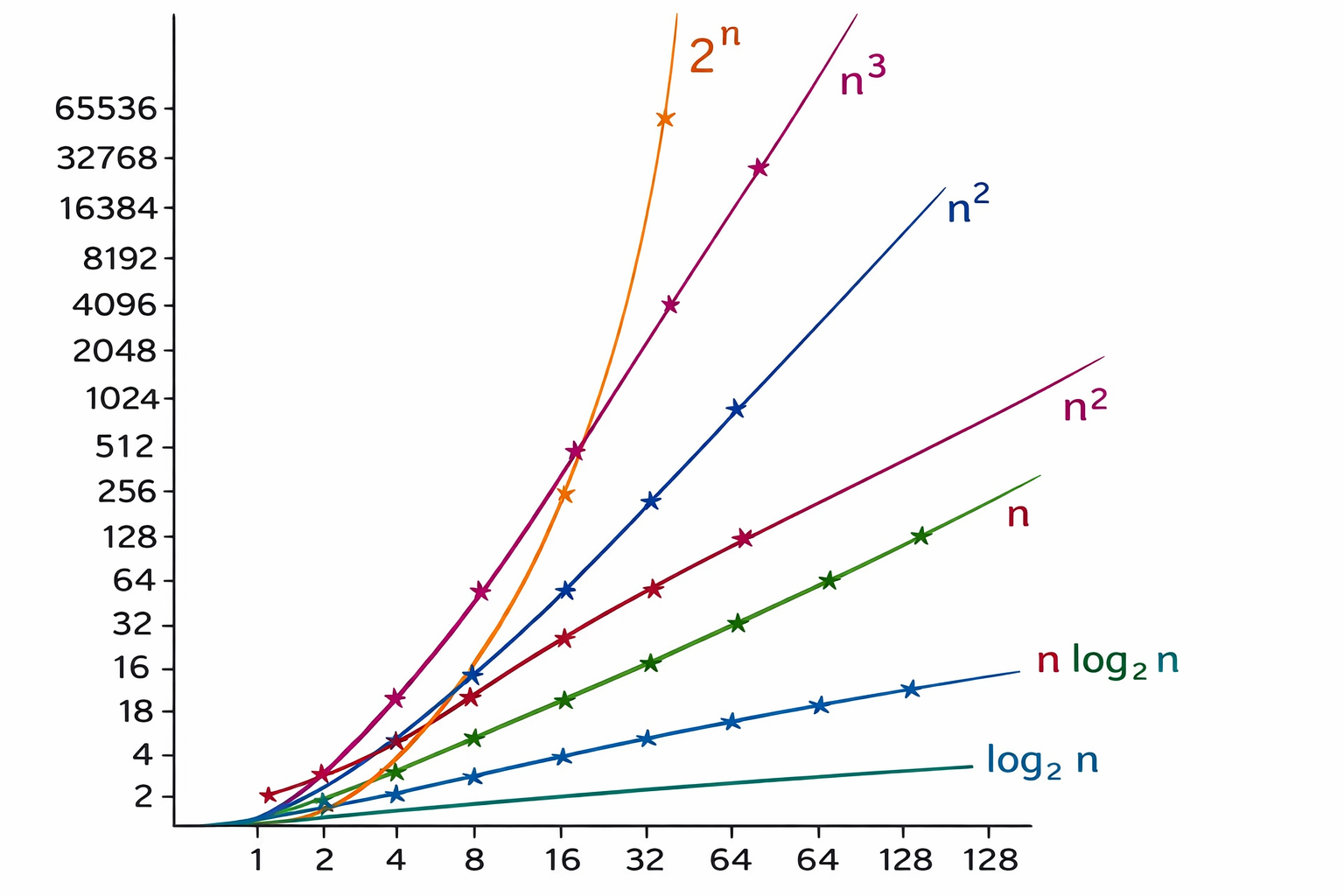
En ingeniería y computación, el rendimiento no es cuestión de suerte. Para medirlo, recurrimos a la teoría del análisis asintótico de funciones, que nos permite predecir cómo crecerá el esfuerzo de cálculo a medida que aumenta la dimensión del problema (n). Para un especialista, no basta con saber cuánto tarda un algoritmo de media; lo vital es el análisis del peor caso. Este define el coste máximo de aplicar el algoritmo a cualquier problema de tamaño n.
Aquí es donde la matemática se vuelve tangible. Imagine que n representa el número de ciudades que un camión debe visitar.
- Complejidad polinómica (O(n^k)): El tiempo crece de forma controlada. Estos problemas se consideran «resolubles eficientemente».
- Complejidad exponencial: El tiempo de cálculo aumenta de forma exponencial. Un ligero aumento en el número de ciudades puede hacer que el ordenador necesite más tiempo que la edad del universo para hallar la respuesta.
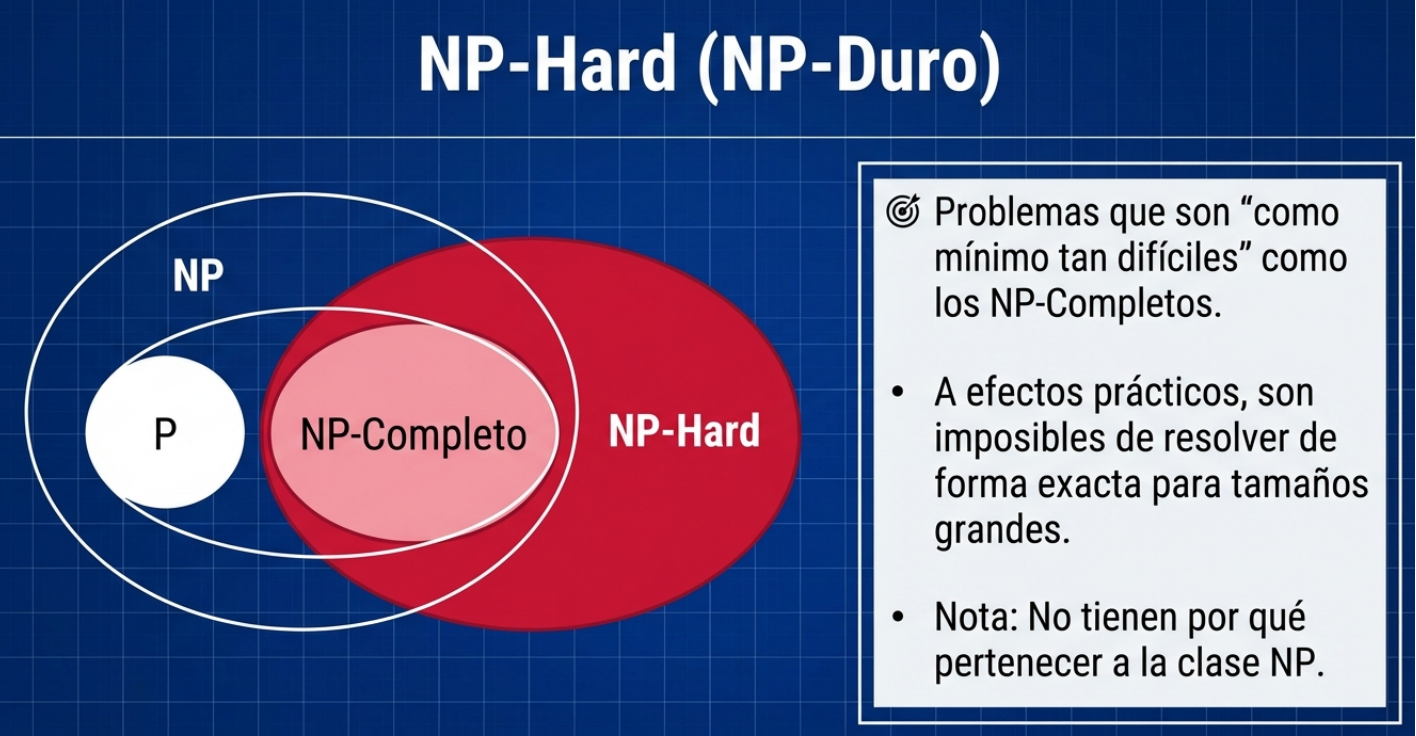
4. El drama de los problemas NP-completos.
Dentro del vasto territorio de la clase NP, existe una «aristocracia» del caos: los problemas NP-completos (NPC). El ejemplo más célebre es el problema del viajante (O(n² 2^n)). Estos problemas son fascinantes porque están interconectados: si alguien lograra encontrar un algoritmo polinómico para resolver un problema NPC, automáticamente todos los problemas NP pasarían a ser resolubles de manera eficiente.
Mientras ese día no llegue, los problemas NPC representan el muro contra el que choca la potencia bruta. En ellos, añadir un solo dato más a la entrada no solo implica trabajo, sino que multiplica la dificultad hasta el punto de que la realidad física se vuelve incapaz de soportar el cálculo.
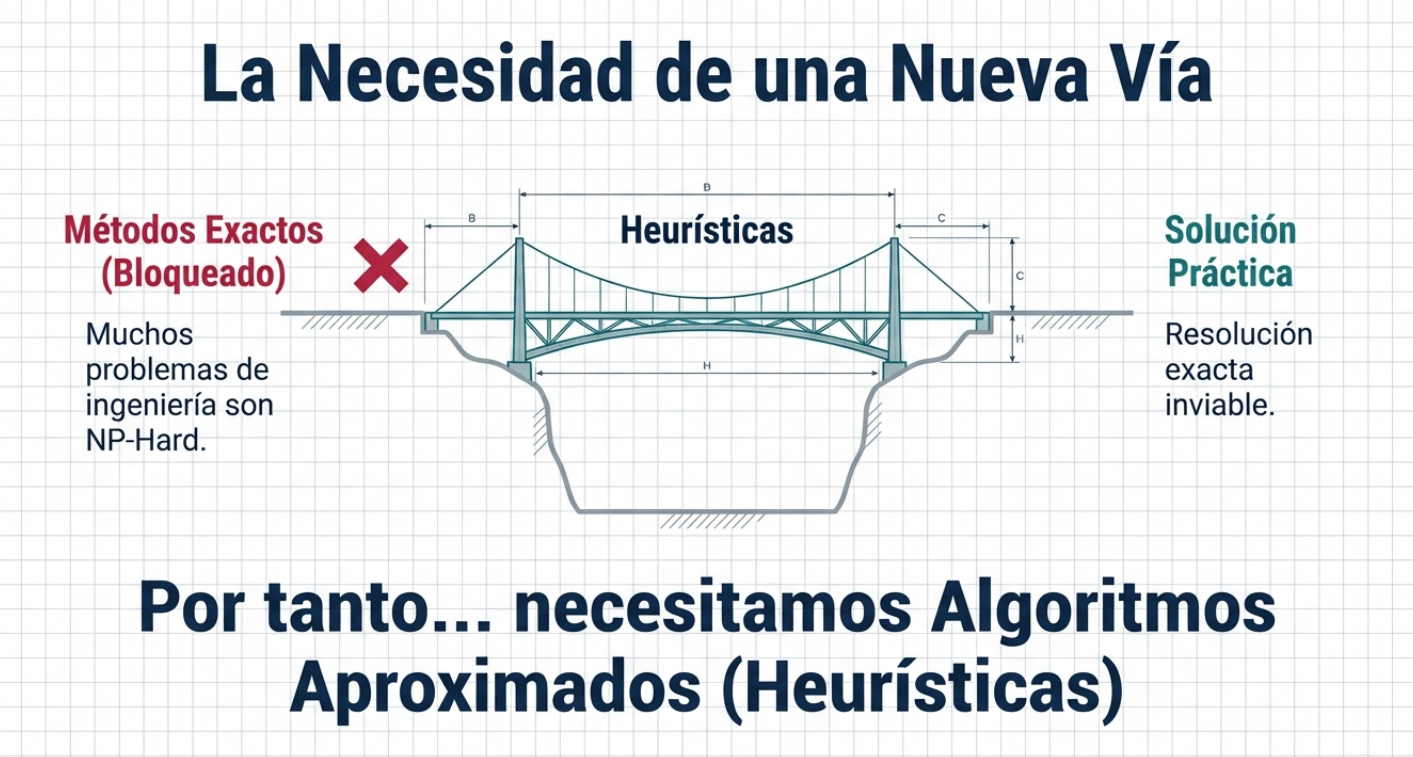
5. El arte de la heurística: la sabiduría de lo «suficientemente bueno».
¿Qué debe hacer un ingeniero ante un problema cuya solución perfecta tardaría milenios en aparecer? La respuesta está en las heurísticas y las metaheurísticas. Se trata de algoritmos aproximados que actúan como un «Plan B» inteligente cuando la perfección se convierte en el enemigo de lo posible.
Sin embargo, el orden de los factores sí altera el producto. Si un problema de optimización se presenta en forma algebraica, es imperativo intentar primero las técnicas clásicas. No tiene sentido utilizar una heurística si los métodos Simplex (para problemas lineales) o de gradiente (para problemas no lineales) pueden proporcionarnos la respuesta exacta. Solo cuando estas herramientas fallan o su lentitud resulta inasumible, recurrimos a la intuición algorítmica.
Conclusión: Hacia una nueva frontera de optimización.
El viaje desde las antiguas reglas de cálculo hasta la optimización de las estructuras de hormigón modernas nos enseña que el límite de la ingeniería no está en la potencia de los procesadores, sino en la elegancia de nuestros métodos. El éxito consiste en saber navegar entre el rigor asintótico y la flexibilidad heurística.
En última instancia, nos enfrentamos a una pregunta que definirá el futuro de nuestra capacidad técnica: ¿residirá el progreso en la búsqueda incansable del algoritmo perfecto que demuestre que P = NP o en perfeccionar nuestra capacidad para utilizar la intuición heurística y construir un mundo «suficientemente bueno» antes de que se agote el tiempo?
En esta conversación podéis escuchar las ideas más interesantes sobre este tema.
El vídeo resume bien los conceptos más importantes de la algoritmia y la complejidad computacional.
Aquí os dejo un resumen de este asunto.
Algorithmic_Complexity_and_Structural_Optimization
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.