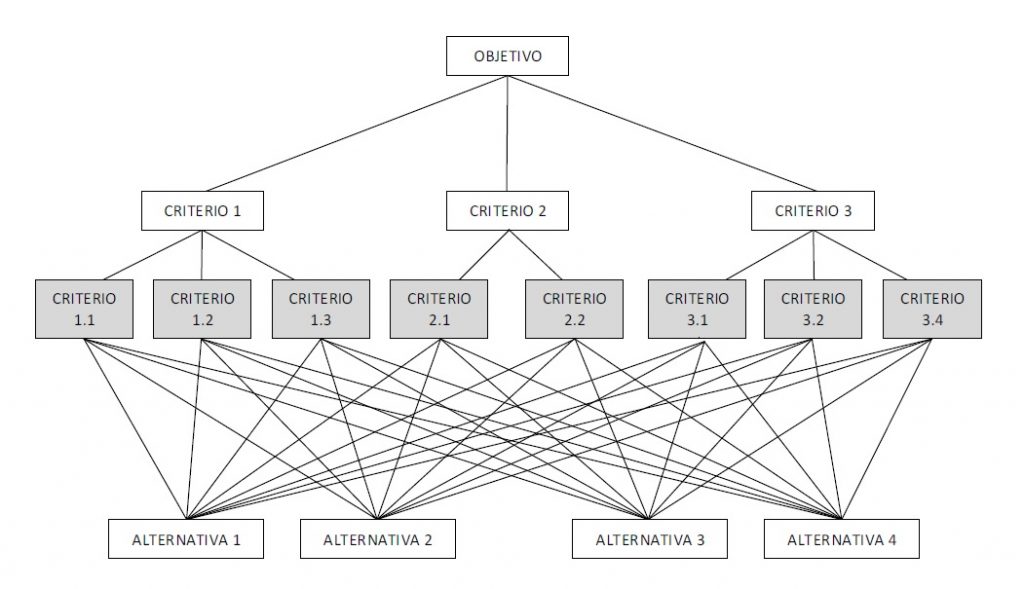
Cuando el profesor Thomas Saaty dió a conocer el método AHP (Analytic Hierarchy Process) en la década de los 80, ya se dio cuenta de que este procedimiento presentaba algunas limitaciones que debía solucionar más adelante. En el año 1996 presentó el modelo ANP (Analytic Network Process) como una generalización de AHP. Este modelo permitió incluir relaciones de interdependencia y realimentación entre elementos del sistema (criterios y alternativas).
En este artículo nos vamos a centrar en algunas limitaciones de AHP que conviene tener en cuenta al tomar decisiones. Este aspecto no es menor, puesto que existen modelos basados en AHP que pueden verse arrastrados por alguna de estas limitaciones.
No obstante, no todo son inconvenientes, ni mucho menos. El profesor José María Moreno ya nos advierte, tal y como se desprende del artículo que os dejo al final de este post, que en este momento no se ha podido probar la supremacía de ningún método o escuela de pensamiento en lo que se refiere al paradigma de la toma de decisión multicriterio. De hecho, AHP ha basado su éxito en trasladar las percepciones humanas a valores numéricos evaluados en una escala de prioridades que permiten sintentizar lo tangible y lo intangible, lo objetivo y lo subjetivo, e incluso lo racional y lo emocional. Además, constituye un procedimiento fácil de utilizar, aplicable a numerosas situaciones reales donde se trata de elegir una alternativa, y donde se puede agregar la decisión individual y la de grupo. Y no menos importante, el AHP es una de las pocas técnicas multicriterio que ofrece una axiomática teórica. Pero veamos ahora en algunos de los inconvenientes de AHP que habrá que valorar siempre que usemos este método o algún otro basado en él.
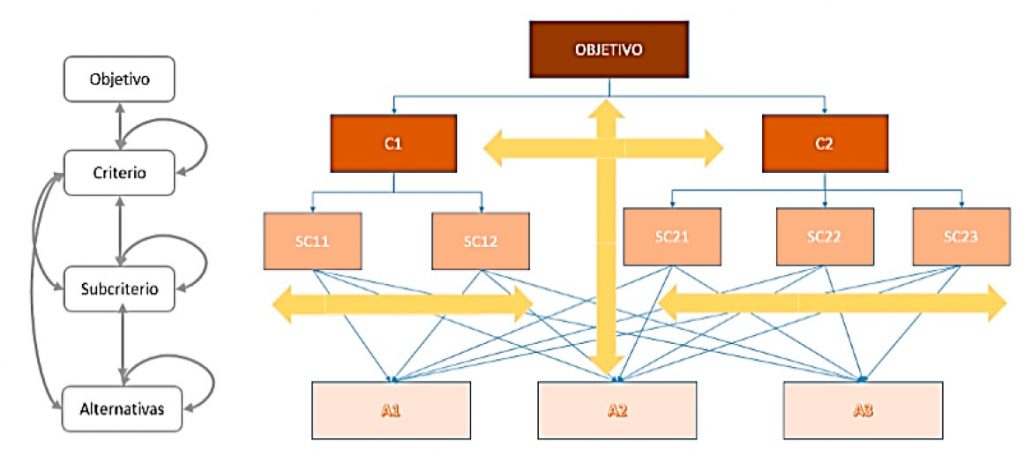
El principal problema que presenta AHP es que, de forma habitual, existen relaciones de interdependencia y realimentación entre los distintos criterios, subcriterios o alternativas (Figura 2). AHP es unidireccional, siendo las relaciones entre los distintos elementos de abajo hacia arriba, lo cual puede suponer una simplificación demasiado fuerte de la realidad. La condición de independencia y jerarquía que subyace en AHP es necesaria para que quien toma las decisiones tenga una función de valor aditiva. De hecho, AHP se apoya en los axiomas de reciprocidad, homogeneidad y síntesis. Pues este último axioma, que implica que los juicios acerca de las prioridades de los elementos en una jerarquía no dependen de los del nivel más bajo, puede rebatirse cuando existe dependencia de la importancia de un objetivo con el nivel inferior.
Veamos un ejemplo concreto. Si se está analizando la sostenibilidad económica, ambiental y social de una estructura de hormigón, uno de los subcriterios económicos puede ser el coste de la estructura y otro subcriterio ambiental puede ser el consumo de recursos, por ejemplo, la cantidad utilizada de hormigón o de acero. Es evidente que el coste depende de la cantidad de recursos consumidos. Este es un ejemplo muy sencillo, pero en el mundo real, las interdependencias pueden ser sutiles o difíciles de ver a priori. No es fácil, en situaciones normales, encontrar criterios y subcriterios que sean independientes unos de otros.
Una de las objeciones recibidas por el método es que si la jerarquía en AHP es incompleta, pueden distorsionarse los pesos. Otro problema adicional tiene que ver con el número de criterios en cada nivel y con su ponderación relativa. Supongamos, por ejemplo que hay dos criterios en el primer nivel y que sus pesos son del 75% en uno y del 25% en el otro. Esta ponderación ya condiciona de forma drástica las ponderaciones de todas las variables que cuelgan de ellas. De esta manera, prácticamente se está anulando el interés de los subcriterios que dependen jerárquicamente de aquel menos ponderado en el primer nivel. El profesor Aznar (2012) ilustra, con ejemplos concretos, cómo el uso de ANP, frente a AHP, provoca cambios significativos en la valoración final de cada una de las alternativas.
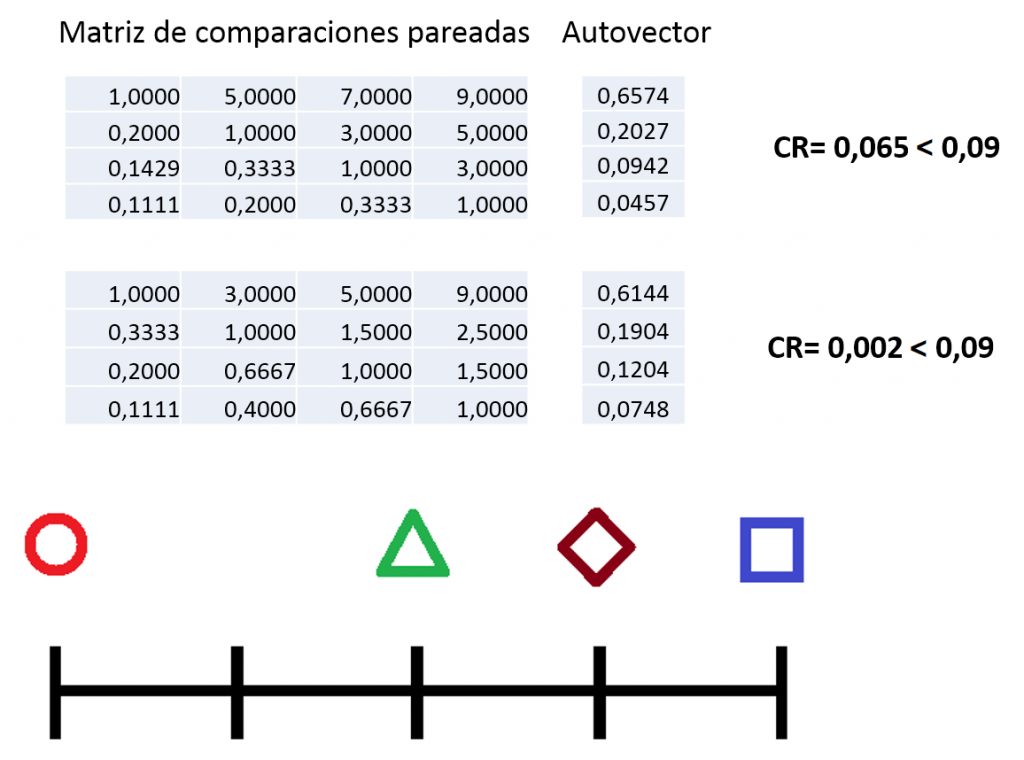
También hay que indicar que la escala de nueve puntos de Saaty (los valores siempre entre 1 y 9) es arbitraria para medir las preferencias de los decisores. Esta escala puede plantear, por ejemplo, el siguiente problema: Si una alternativa A es 5 veces más importante que la alternativa B y esta a su vez es 5 veces más importante que la alternativa C, se produce un problema serio, ya que AHP no puede manejar el hecho de que la alternativa A es 25 veces más importante que la alternativa C. Esta deficiencia se visualiza en la Figura 3. Se puede ver cómo la alternativa círculo rojo es mejor al resto con la escala de Saaty: 5 para el triángulo, 7 para el rombo y 9 para el cuadrado. Si comparamos el triángulo verde con el resto, debería ser: 3 para el rombo y 5 para el cuadrado. Del mismo modo, el rombo presenta una valoración de 3 respecto al cuadrado. Con esta matriz pareada, el ratio de consistencia es válido. Sin embargo, si se reajustan las valoraciones dividiendo por dos las comparaciones del triángulo, rombo y cuadrado, el ratio de consistencia baja significativamente. En ese caso, los autovectores han cambiado, aunque se mantienen las prioridades.
Pero aquí no terminan los inconvenientes. Como contrapartida a la simplicidad, AHP no tiene en cuenta la incerteza asociada a representar la opinión en la forma de un número. Además, si se agrega durante el proceso otra alternativa, las clasificaciones de las alternativas originales pueden cambiar, lo cual rigidiza el método. Por otra parte, si se incrementa el número de alternativas o criterios, se puede llegar a la inconsistencia de la matriz de comparaciones pareadas. Asimismo, en el método es muy laborioso si se incrementa el número de alternativas o criterios.
Un inconveniente adicional de AHP es la normalización de las matrices de preferencias, transformando las valoraciones planteadas en utilidades definidas en la escala (0,1) mediante la obtención del vector propio de las mismas. Esto solo es estrictamente válido si los juicios volcados en la matriz son perfectamente consistentes. En caso contrario, puede ser complicada la interpretación.
Sin embargo, los problemas con AHP se agudizan cuando aparece una situación de conflicto en la que existe una mayor o menor oposición en los intereses de los decisores y, además, las decisiones de cada decisor dependen de las que tomen los demás en la búsqueda de sus propios intereses. En este caso, la teoría de juegos o juegos de estrategia sería la forma más razonable de abordar el problema.
En apretada síntesis, estas reflexiones vienen a cuento de que, muchas veces, estamos utilizando métodos, incluso recogidas alguna normativa legal, donde se pretende dar cuerpo de ley a un conjunto de criterios para evaluar algún aspecto de especial interés. Es el caso del método AHP empleado, por ejemplo, como parte de otros como MIVES, que han dado lugar, a un índice de contribución de la estructura a la sostenibilidad (Anejo 2 del Código Estructural). Con todo, y para tranquilidad de muchos, la teoría AHP, si bien presenta ciertos problemas como los expuestos, parece conservar su condición de ser el método de toma de decisión más conocido y empleado de los métodos multicriterio.
También, por su interés, os dejo el artículo de José Luis Zanazzi sobre las críticas recibidas por AHP y su análisis.
Pero no todo van a ser noticias negativas en relación con el AHP. Os dejo, a continuación, el artículo del profesor José María Moreno donde explica el método AHP.
Referencias:
AZNAR, J.; GUIJARRO, F. (2012). Nuevos métodos de valoración: modelos multicriterio. Editorial Universitat Politècnica de València.
SAATY, T.L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.