El uso de calculadoras electrónicas y ordenadores nos hace perder el orden de magnitud de un problema. Como ya comenté en un artículo anterior, el uso masivo de herramientas informáticas atrofian la capacidad intuitiva y de cálculo de los futuros profesionales. Un buen ingeniero o científico debería tener un “número gordo” del resultado antes, incluso, de resolver un problema.
Cuando se miden ciertas cantidades, lo valores medidos se conocen solo dentro de los límites de la incertidumbre experimental. Usamos el número de cifras significativas como una medición que sirve para expresar algo de dicha incertidumbre. De hecho, todas las cifras significativas importan información veraz de la medición, excepto la última, que es incierta.
Para conocer el número correcto de cifras significativas, se siguen las siguientes normas:
- Los ceros situados en medio de números diferentes de cero son significativos, por ejemplo, 709 cm tiene tres cifras significativas.
- Los ceros a la izquierda del primer número no son significativos, por ejemplo, 0,000057 presenta dos cifras significativas.
- Para los números mayores que uno, los ceros escritos a la derecha de la coma decimal también cuentan como cifras significativas, por ejemplo 6,0 tiene dos cifras significativas.
- En los números enteros, los ceros situados después de un dígito distinto de cero, pueden ser o no cifras significativas, por ejemplo 8000, puede tener una cifra significativa (el número 8), pero también cuatro. Para evitar el problema se puede usar la notación científica, indicando el número 8000 como 8·103 teniendo solo una cifra significativa (el número 8) o 8,0·103, tenemos dos cifras significativas (8,0).
Existen reglas empíricas que permiten conocer el número de cifras significativas en el caso de operaciones básicas:
- Cuando se multiplican o dividen varias cifras, el resultado tiene el mismo número de cifras significativas que el número de menor cifras significativas
- Cuando dos números se sumen o resten, el número de lugares decimales en el resultado debe ser igual al número más pequeño de lugares decimales de cualquier término en la suma
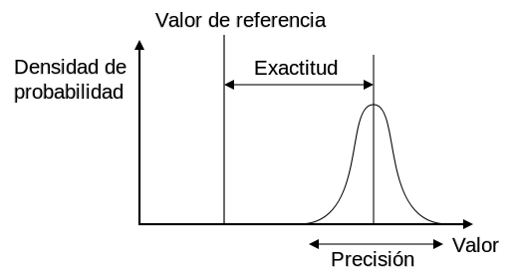
El error de medición se define como la diferencia entre el valor medido y el “valor verdadero”. Los errores de medición afectan a cualquier instrumento de medición y pueden deberse a distintas causas. Las que se pueden de alguna manera prever, calcular, eliminar mediante calibraciones y compensaciones, se denominan deterministas o sistemáticos y se relacionan con la exactitud de las mediciones. Los que no se pueden prever, pues dependen de causas desconocidas, o estocásticas se denominan aleatorios y están relacionados con la precisión del instrumento.
Sin embargo, para establecer el error en una medida, se debe disponer, junto con la medida de la magnitud, su error y la unidad de medida del Sistema Internacional. En este caso, se deben seguir las siguientes normas:
- El error se da con una sola cifra significativa. Se trata del primer dígito comenzando por la izquierda distinto de cero, redondeando por exceso en una unidad si la segunda cifra es 5 o mayor de 5. Sin embargo, como excepción se dan dos cifras significativas para el error si la primera cifra significativa es 1, o bien siendo la primera un 2, la segunda no llega a 5.
- La última cifra significativa en el valor de una magnitud física y su error, expresados en las mismas unidades, deben de corresponder al mismo orden de magnitud (centenas, decenas, unidades, décimas, centésimas).
Con una sola medida, se indica el error instrumental, que es la mitad de la menor división de la escala del instrumento usado. Sin embargo, con n medidas directas consecutivas, se considera el error cuadrático de la media (una desviación estándar de la población de las medias). A todo caso, se utilizará el mayor de ambos errores.
En este vídeo explico los aspectos básicos de los errores de medición:
Por otra parte, hay que conocer que los errores se propagan cuando hacemos operaciones matemáticas. Simplificando, cuando tenemos sumas o restas, las cotas de error absoluto se suman; cuando hay productos o divisiones, las cotas de error relativo se suman.
Pero mejor será que os deje un vídeo explicativo del profesor de la UPV, Marcos Herminio Jiménez Valentín. Espero que os aclare este tema.
Este otro vídeo también es de interés para conocer con mayor profundidad la propagación de los errores.
Os dejo también unos pequeños apuntes del profesor Antonio Miguel Posadas Chinchilla, de la Universidad de Almería, que os podéis descargar de este enlace: https://w3.ual.es/~aposadas/TeoriaErrores.pdf
