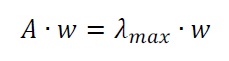En numerosas ocasiones contamos con muy poca información o tenemos que tomar una decisión teniendo en cuenta aspectos cualitativos que son difíciles de valorar. Para solucionar este tipo de problemas, muy habituales en situaciones reales, el profesor Thomas L. Saaty propuso en la década de los 70 un método denominado Analytic Hierarchy Process (AHP), que se ha traducido al español como Proceso Analítico Jerárquico. Este método multiatributo, nacido como respuesta a problemas concretos de toma de decisiones en el Departamento de Defensa de los Estados Unidos, hoy día se aplica habitualmente a casi todos los ámbitos de la empresa, la economía o la investigación de operaciones, entre otros muchos.
En apretada síntesis, AHP es un método que selecciona alternativas en función de una serie de criterios o variables, normalmente jerarquizados, los cuales suelen entrar en conflicto. En esta estructura jerárquica, el objetivo final se encuentra en el nivel más elevado, y los criterios y subcriterios en los niveles inferiores, tal y como se muestra en la Figura 2. Para que el método sea eficaz, es fundamental elegir bien los criterios y subcriterios, los cuales deben estar muy bien definidos, ser relevantes y mutuamente excluyentes (independencia entre ellos). Es importante que el número de criterios y subcriterios en cada nivel no sea superior a 7, para evitar excesivas comparaciones a pares.

Una vez definida la estructura jerárquica, se comparan los criterios de cada grupo del mismo nivel jerárquico y la comparación directa por pares de las alternativas respecto a los criterios del nivel inferior. Para ello se utilizan matrices de comparación pareadas usando una Escala Fundamental (Tabla 1). Esta es la clave del método, usar una escala de comparación por pares, puesto que el cerebro humano está especialmente bien diseñado para comparar dos criterios o alternativas entre sí, pero menos cuando tiene que hacer comparaciones conjuntas. En efecto, la Ley de Weber-Fechner establece que el menor cambio discernible en la magnitud de un estímulo es proporcional a la magnitud de dicho estímulo. Como la relación entre el estímulo y la percepción corresponde a una escala logarítmica, si un estímulo crece en progresión geométrica, la percepción evolucionará como una progresión aritmética. Es por ello que AHP utiliza una escala fundamental del 1 al 9 que ha sido satisfactoria en comprobaciones empíricas realizadas en situaciones reales muy diversas.

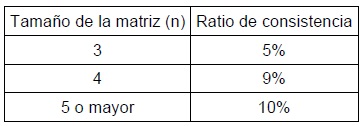
La comparación de las diferentes alternativas respecto al criterio del nivel inferior de la estructura jerárquica, como la comparación de los diferentes criterios de un mismo nivel jerárquico dan lugar a una matriz cuadrada denominada matriz de decisión. Esta matriz cumple con las propiedades de reciprocidad (si aij=x, entonces aji=1/x), homogeneidad (si i y j son igualmente importantes, aij=aji=1, y además, aii= 1 para todo i), y consistencia (la matriz no debe contener contradicciones en la valoración realizada). La consistencia se obtiene mediante el índice de consistencia (Consistency Index, CI) donde λmax es el máximo autovalor y n es la dimensión de la matriz de decisión. Un índice de consistencia igual a cero significa que la consistencia es completa. Una vez obtenido CI, se obtiene la proporción de consistencia (Consistency Ratio, CR) siendo aceptado siempre que no supere los valores indicados en la Tabla 3. Si en una matriz se supera el CR máximo, hay que revisar las ponderaciones.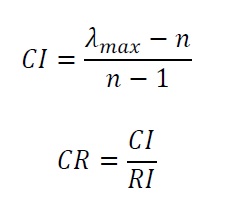
Donde RI es el índice aleatorio, que indica la consistencia de una matriz aleatoria (Tabla 2):

Una vez verificada la consistencia, se obtienen los pesos, que representan la importancia relativa de cada criterio o las prioridades de las diferentes alternativas respecto a un determinado criterio. Para ello, el AHP original utiliza el método de los autovalores, donde hay que resolver la siguiente ecuación:
donde A representa la matriz de comparación, w el autovector o vector de preferencia, y λmax el autovalor.
A continuación os dejo algunos vídeos de interés donde se explica el método AHP y sus aplicaciones. Espero que os sean de utilidad.
Referencias:
Saaty, T.L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.