Jorge Luis Borges imaginó una vez un imperio en el que el arte de la cartografía alcanzó tal perfección que el mapa de una sola provincia ocupaba toda una ciudad. Finalmente, los cartógrafos trazaron un mapa del imperio que tenía el mismo tamaño que este y coincidía punto por punto con él. Por supuesto, aquel mapa era inútil.
En ciencia sucede algo similar: medir no es replicar la realidad, sino crear un mapa de ella. Estamos obsesionados con la exactitud, pero en el laboratorio pronto aprendemos que la «medida exacta» es una quimera. Medir no consiste en capturar una verdad absoluta, sino en gestionar con elegancia la incertidumbre. Un dato sin su margen de error no es una medida, sino una simple expresión de deseos.
1. La ilusión de la exactitud: el error es inevitable.
En metrología, la humildad es una competencia técnica. Debemos aceptar que nuestros sentidos y nuestros instrumentos están limitados por definición. La teoría de los errores nos enseña que el «valor verdadero» es un ideal matemático al que solo podemos aproximarnos. El error no es una equivocación del científico, sino una propiedad inherente al acto de medir.
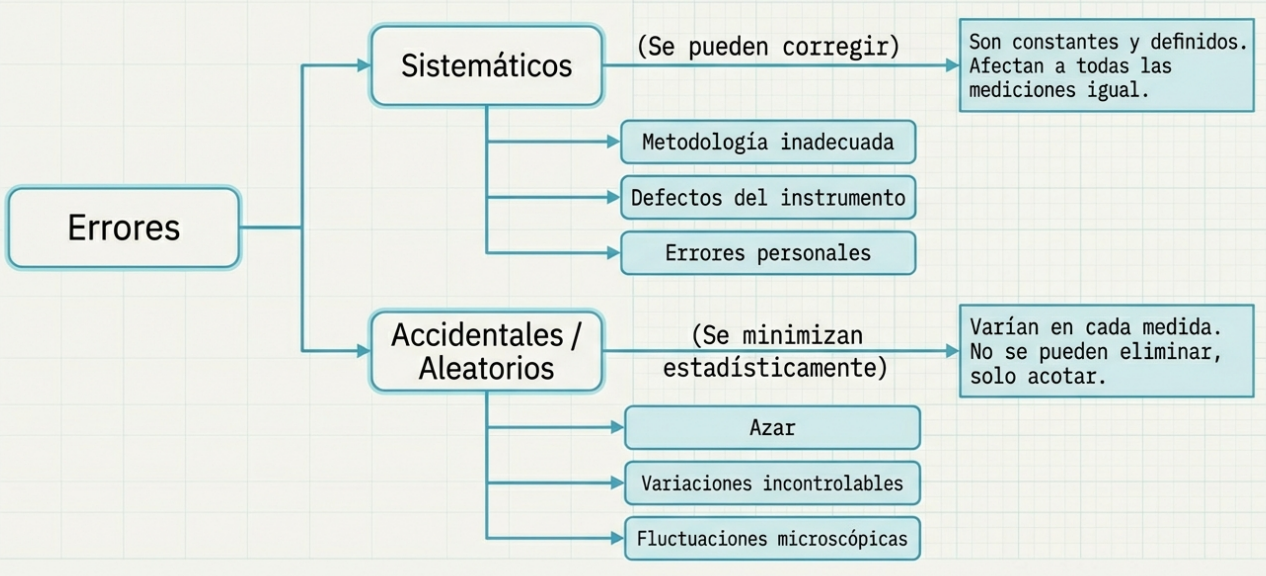
Existen dos fuerzas que distorsionan nuestro «mapa» de la realidad:
- El error sistemático es un sesgo constante. Aparece cuando la metodología es inadecuada, los instrumentos están mal calibrados o los patrones de medición son dudosos. Se trata de un error predecible que desplaza todas nuestras mediciones en la misma dirección, alejándolas de la realidad.
- El error accidental o aleatorio es el «ruido» del universo. Se debe al azar, a variaciones microscópicas y a factores incontrolables. Se manifiestan como pequeñas fluctuaciones al repetir una medición y, aunque no pueden eliminarse, la estadística es nuestra herramienta para controlarlas.
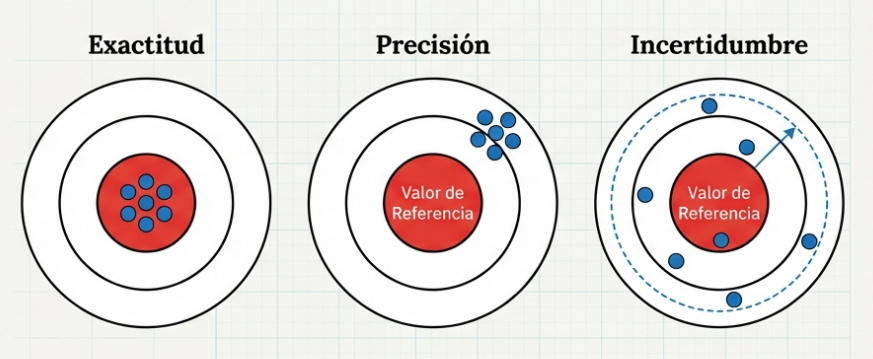
Para navegar por esta complejidad, distinguimos entre exactitud (cuán cerca está nuestra flecha del centro de la diana) y precisión (cuán cerca están las flechas entre sí, independientemente de dónde hayan caído).
«El error se define como la diferencia entre el valor verdadero y el obtenido experimentalmente».
2. El drama de los ceros: el límite de nuestro conocimiento.
En el lenguaje técnico, los números no solo indican cantidades, sino que también expresan confianza. No es lo mismo informar de un peso de «1,5 g» que de uno de «1,500 g». Las cifras significativas son los dígitos que realmente aportan información sobre la precisión de nuestra medición.
Para entenderlas, seguimos unas reglas claras:
- Cualquier dígito distinto de cero es significativo.
- Los ceros situados entre dígitos significativos (por ejemplo, 2,054) siempre cuentan.
- Los ceros a la izquierda (por ejemplo, 0,076) son solo marcadores de posición decimal.
- Los ceros situados a la derecha del punto decimal (por ejemplo, 0,0540) son fundamentales, ya que indican que el instrumento fue capaz de medir esa posición.
El número «1500» es el ejemplo clásico de ambigüedad: ¿es una aproximación a la centena o una medida exacta en gramos? La notación científica resuelve el misterio: 1,5 × 10^(3) indica dos cifras significativas, mientras que 1,500 × 10^(3) indica cuatro. Aquí reside una reflexión profunda: la última cifra significativa siempre es incierta. Es el límite de nuestra visión, el punto en el que nuestra capacidad de observación se desvanece en la duda.
3. La paradoja de la resta: el «caso más desfavorable».
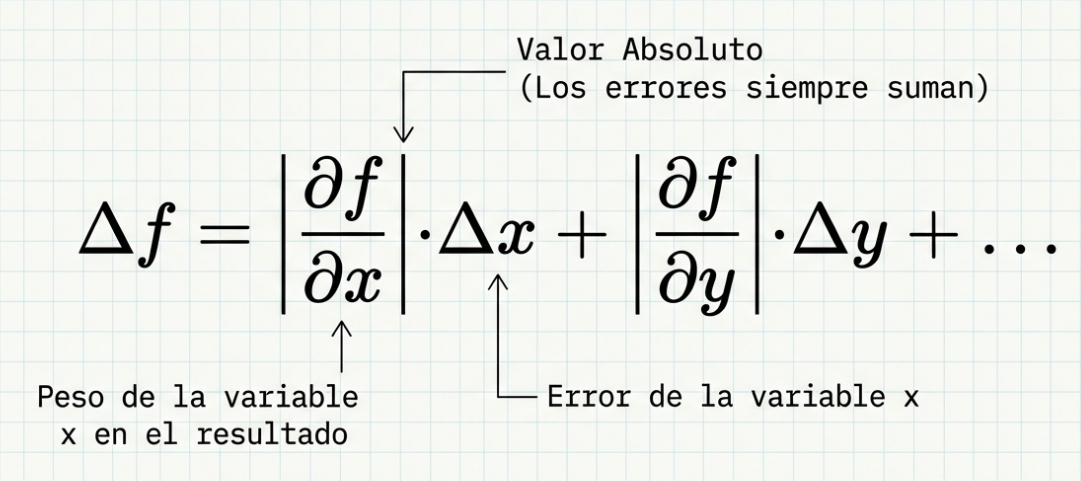
Uno de los conceptos más fascinantes y contraintuitivos es la propagación de errores. Imaginemos que pesamos una tetera colocando pesas en un platillo. Si la masa de la tetera se obtiene restando la masa del plato de la masa total, podrías pensar que los errores también se restan. Sin embargo, la ciencia es conservadora por necesidad.
En metrología, trabajamos bajo la filosofía del caso más desfavorable. Si la medida A presenta un error por exceso y la medida B, por defecto, al restarlas (A – B) el error total resultante no disminuye, sino que aumenta. Las incertidumbres nunca se anulan; siempre se acumulan.
- En sumas y restas, las cotas de error absoluto se suman.
- En multiplicaciones y divisiones, lo que sumamos son los errores relativos.
Cuando multiplicamos, no solo añadimos «milímetros» de duda, sino que también multiplicamos la incertidumbre de la proporción misma, lo que amplía el margen de error de nuestro mapa original.
4. La regla de oro: la estética del rigor.
La honestidad metrológica tiene una regla estética: el error absoluto generalmente se expresa con una sola cifra significativa. No tiene sentido decir que una montaña mide 2000,432 metros, con un error de 12,45 metros. La duda en las decenas anula cualquier certeza en los milímetros.
Sin embargo, existen dos excepciones en las que se permiten dos cifras significativas en el error:
- Si la primera cifra es un 1.
- Si la primera cifra es un 2 seguido de una cifra menor que 5 (es decir, hasta 24).
La regla del redondeo es estricta: se redondea por exceso en una unidad si la segunda cifra es 5 o superior. Finalmente, el valor y su error deben tener el mismo número de decimales.
Corrección de estilo metrológico
5. El criterio de dispersión: ¿cuándo es suficiente?
¿Cuántas mediciones necesitamos para que nuestra media sea fiable? Si solo realizamos una medición, el error dependerá directamente del instrumento.
- En los instrumentos digitales, el error se expresa como la sensibilidad (S).
- En los instrumentos analógicos, el error es la mitad de la sensibilidad (S/2).
Pero cuando la precisión es crítica, recurrimos a la estadística. El proceso siempre comienza con 3 medidas iniciales para calcular el criterio de dispersión (T):
Para series largas (N ≥ 15), utilizamos el error cuadrático medio (ECM). Este cálculo parte de la suposición de que nuestros datos siguen una distribución gaussiana (la famosa campana de Gauss), según la cual el 68,3 % de las medidas se encontrarán dentro de un margen de error cuadrático medio respecto a la media. Es el reconocimiento matemático de que el azar tiene una estructura.
Conclusión: la honestidad de la incertidumbre.
La ciencia no es el dominio de las verdades absolutas, sino el territorio de la incertidumbre controlada. Aceptar el error, nombrarlo y calcularlo no es una debilidad, sino la máxima expresión de la integridad técnica. Al acotar lo que no sabemos, protegemos la validez de lo que sí sabemos.
¿Cómo cambiaría nuestra percepción del mundo si aceptáramos que cada «dato real» que consumimos, desde las estadísticas económicas hasta los resultados de un análisis clínico, viene acompañado de un margen de error invisible? Quizás dejaríamos de buscar certezas absolutas y empezaríamos a valorar la honestidad de la duda bien calculada.
En esta conversación puedes escuchar las ideas más interesantes de este artículo.
Aquí tienes un resumen en formato de vídeo sobre los aspectos clave de la medición.
Por último, creo que este resumen puede resultar de interés.
[gview file=»https://victoryepes.blogs.upv.es/wp-content/uploads/2026/02/Medicion_y_error_La_guia_maestra.pdf»]
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.