1. Introducción: ¿estás escuchando lo que tus datos te dicen?
1. Introducción: ¿estás escuchando lo que tus datos te dicen?
Vivimos en un mundo saturado de información. Gráficos, porcentajes y hojas de cálculo nos rodean prometiendo respuestas. Sin embargo, a menudo nos quedamos en la superficie, sin saber cómo interpretar el verdadero mensaje que se esconde tras los números. ¿Qué pasaría si pudieras «escuchar» las historias que tus datos ansían contar?
Aquí es donde entra en juego el análisis exploratorio de datos (AED). Más que una ciencia rígida, es el arte de la investigación, un trabajo de detective que nos permite dialogar con la información. Se trata de buscar patrones, descubrir anomalías y formular preguntas sin la presión de obtener una respuesta definitiva.
En este artículo, descubriremos cuatro de las ideas más impactantes y, en ocasiones, contraintuitivas que revela este enfoque. Para ello, seguiremos un proceso de cuatro pasos para pensar como un detective de datos: primero, adoptaremos la mentalidad adecuada; segundo, conoceremos la «personalidad» de nuestros datos; tercero, aprenderemos a distinguir lo normal de lo anómalo, y, por último, descubriremos una ley casi mágica que hace posibles las predicciones.
2. El análisis es un diálogo informal, no un veredicto final.
A diferencia de la percepción popular de la estadística como un campo de verdades absolutas y reglas inflexibles, el análisis exploratorio de datos se basa en la exploración sin restricciones. Su objetivo principal no es emitir un juicio final e irrefutable, sino buscar regularidades interesantes y pistas que requieran una investigación más profunda.
Es crucial entender que las conclusiones extraídas en esta fase son informales y se aplican de manera muy específica. Como señala uno de sus principios fundamentales: «Las conclusiones solo se aplican a los individuos y a las circunstancias para las que se obtuvieron los datos». No se trata de generalizar a toda una población, sino de comprender en profundidad la muestra que tenemos delante.
Las conclusiones son informales y se basan en lo que vemos en los datos.
Esta idea resulta increíblemente liberadora. Nos permite ser curiosos, seguir nuestra intuición y buscar patrones sin la presión de «demostrar» formalmente una hipótesis desde el primer momento. Es el primer paso para alcanzar una comprensión genuina, un diálogo abierto con la información antes de emitir un veredicto. Con esta mentalidad, ya estamos listos para conocer a nuestro «sospechoso»: el conjunto de datos.
3. La «forma» de tus datos tiene personalidad propia.
Un conjunto de datos no es solo una lista de números, sino que tiene una forma visual que revela su carácter. Entender esta forma es uno de los primeros y más importantes pasos, ya que nos indica cómo se agrupan los valores y dónde se concentran. Los dos rasgos principales de esta personalidad son la asimetría y la curtosis.
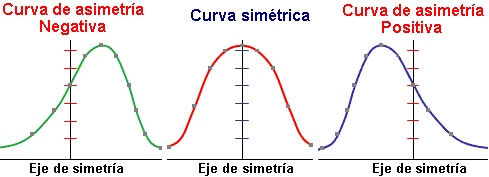
La asimetría nos indica si los datos están sesgados y la relación entre la media, la mediana y la moda lo revela todo. En una distribución simétrica, los tres valores coinciden. Sin embargo, cuando hay asimetría, se separan. Imagina los salarios en una empresa: la mayoría de los empleados cobra un sueldo similar (la moda), pero el altísimo salario del director ejecutivo (un valor atípico) hace que la media se desplace hacia la derecha. La mediana, que es el valor central, se ve menos afectada. Por eso, en una distribución asimétrica a la derecha (positiva), la media es mayor que la mediana. Este sesgo indica la presencia de valores extremos.
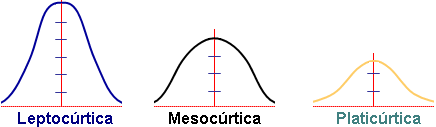
Por otro lado, la curtosis describe hasta qué punto la distribución es «puntiaguda» o «plana». Una distribución leptocúrtica (muy puntiaguda) indica que hay muy poca variación y que la mayoría de los valores se asemejan mucho a la media. Esto puede ser bueno si fabricas tornillos y buscas consistencia, pero malo si analizas los retornos de una inversión, ya que podría indicar un riesgo oculto de un evento extremo. Una distribución platicúrtica (aplanada) indica una gran dispersión de los datos.
Ahora que conocemos la «personalidad» de nuestros datos, podemos utilizar una de las herramientas más comunes para entender su comportamiento: la distribución normal.
4. La regla 68-95-99,7: un atajo mental para entender la normalidad.
La distribución normal, también conocida como «curva de campana», es uno de los patrones más frecuentes en la naturaleza y en el análisis de datos. Desde la altura de las personas hasta los errores de medición, este patrón se repite una y otra vez. Para comprenderla rápidamente, existe una herramienta sumamente útil: la regla empírica 68-95-99,7.
Esta regla nos ofrece un atajo mental para saber cómo se distribuyen los datos alrededor de la media en una distribución normal (las cifras exactas son 68,3 %, 95,4 % y 99,7 %):
- Aproximadamente el 68 % de los datos se encuentran a 1 desviación estándar de la media.
- Aproximadamente el 95 % de los datos se encuentran a 2 desviaciones estándar de la media.
- Aproximadamente el 99,7 % de los datos se encuentran a 3 desviaciones estándar de la media.
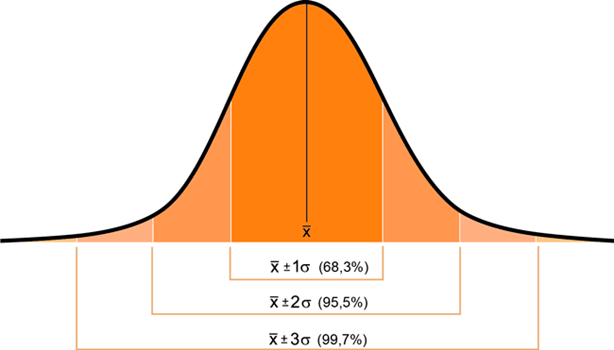
Esta regla es poderosa por su simplicidad. Sin necesidad de realizar cálculos complejos, nos permite estimar con rapidez dónde se encuentran la mayoría de los valores de nuestro conjunto de datos e identificar fácilmente aquellas observaciones que se alejan mucho de la media y, por tanto, podrían ser atípicas.
5. El teorema del límite central: el «milagro» estadístico que lo ordena todo.
Si hay una idea en estadística que parece casi mágica, esa es el teorema del límite central (TLC). Es uno de los conceptos más fundamentales y sorprendentes y la razón por la que podemos hacer inferencias fiables sobre una población entera a partir de una muestra.
La idea sorprendente es la siguiente: da igual lo extraña, sesgada o anormal que sea la distribución de una población original. Si se toman muestras suficientemente grandes de esa población y se calcula la media de cada una, la distribución de esas medias muestrales tiende a ser normal perfecta. Observe la imagen del Teorema del Límite Central en el documento de referencia. Da igual el punto de partida: una distribución uniforme y plana, como en la Población I; una distribución en forma de V, como en la Población II; o una distribución con un gran sesgo, como en la Población III. El resultado es el mismo. Al tomar muestras pequeñas (n = 2 o n = 5), las medias empiezan a agruparse en torno al centro. Cuando el tamaño de la muestra alcanza 30 (n = 30), las tres distribuciones de medias muestrales se asemejan prácticamente a una curva de campana perfecta.
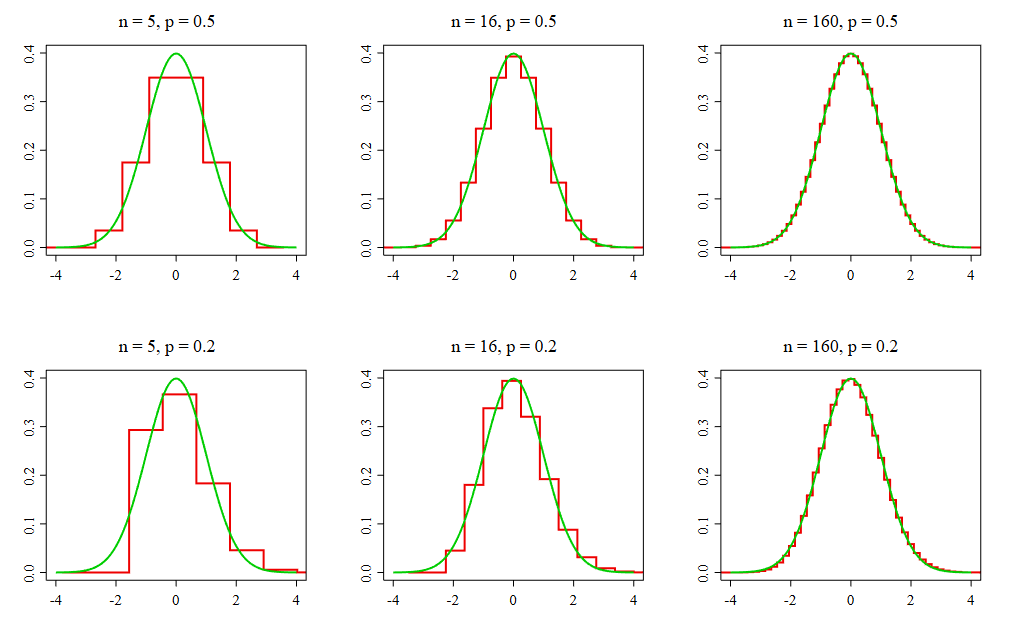
Este fenómeno es asombroso. Es como si un principio de orden universal actuara sobre el caos, lo que nos permite utilizar las propiedades de la distribución normal para hacer predicciones precisas, incluso cuando la fuente de nuestros datos es completamente anárquica. Este teorema es el pilar sobre el que se construye gran parte de la estadística inferencial.
6. Conclusión: de los datos a la sabiduría.
El análisis de datos es mucho más que aplicar fórmulas. Se trata de un proceso de descubrimiento que se apoya en herramientas conceptuales poderosas, accesibles y, a menudo, sorprendentes. Desde comprender que el análisis es una exploración informal hasta apreciar el «milagro» del Teorema del Límite Central, estos conceptos nos capacitan para ir más allá de los números y comenzar a extraer conocimiento real.
La próxima vez que te enfrentes a un conjunto de datos, no te limites a calcular promedios. Míralos con curiosidad, busca su forma, comprende su distribución y escucha atentamente.
¿Qué historia inesperada podrían contarte tus propios datos si te detuvieras a escucharlos?
En esta conversación se presentan las ideas más interesantes sobre este tema.
El siguiente vídeo resume bien la información sobre el análisis exploratorio de datos.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.