proceso analítico jerárquico – El blog de Víctor Yepes

Mejora de la evaluación de la sostenibilidad de puentes en entornos agresivos mediante la decisión grupal multicriterio

Acaban de publicarnos en DYNA, revista indexada en el JCR, un artículo sobre la mejora de la evaluación de la sostenibilidad de puentes en entornos agresivos mediante la decisión grupal multicriterio. Aborda el desafío de combinar las dimensiones económica, ambiental y social en un único indicador holístico para la toma de decisiones en el diseño de infraestructuras. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València.

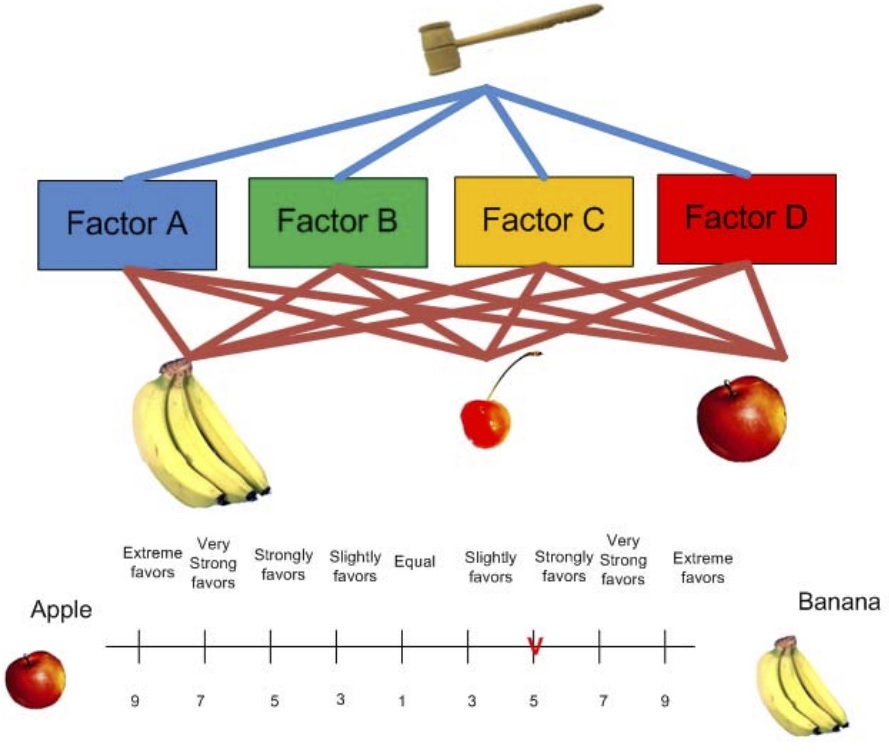
El artículo contribuye al campo de la evaluación de la sostenibilidad de los puentes en entornos agresivos mediante la aplicación de técnicas de toma de decisiones grupales en el ámbito de los criterios múltiples. Aborda el desafío de combinar las dimensiones económica, ambiental y social en un único indicador holístico para la toma de decisiones en el diseño de infraestructuras.
El estudio evalúa cinco alternativas de diseño diferentes para un puente de hormigón expuesto a un entorno costero utilizando cuatro técnicas de toma de decisiones (ANP, TOPSIS, COPRAS y VIKOR). Los resultados indican que los hormigones que contienen pequeñas cantidades de humo de sílice funcionan mejor a lo largo de su ciclo de vida que otras soluciones que suelen aumentar la durabilidad.
La investigación contribuye al desarrollo de herramientas y métodos para evaluar la sostenibilidad de las infraestructuras y guiar las futuras acciones de diseño en diversas estructuras. Se alinea con el enfoque en promover las iniciativas de economía circular y el cumplimiento de los requisitos ambientales y sociales específicos en las licitaciones de proyectos públicos

Abstract:

The construction industry is increasingly recognized as critical in achieving Sustainable Development Goals. Construction activities and infrastructure have both beneficial and non-beneficial impacts, making infrastructure design a focal point of current research investigating how best to contribute to sustainability as society demands. Although methods exist to assess infrastructures’ economic, environmental, and social life cycle, the challenge remains in combining these dimensions into a single holistic indicator to facilitate decision-making. This study applies four decision-making techniques (ANP, TOPSIS, COPRAS, and VIKOR) to evaluate five different design alternatives for a concrete bridge exposed to a coastal environment. The results indicate that concretes containing even small amounts of silica fume perform better over their life cycle than other solutions usually considered to increase durability, such as water/cement ratio reduction or concrete cover increase.

Keywords:

Sustainable design, bridges, life cycle assessment, Analytic Network Process, TOPSIS, VIKOR, COPRAS, Multi-criteria decision-making

Reference:

NAVARRO, I.J.; MARTÍ, J.V.; YEPES, V. (2023). Enhancing sustainability assessment of bridges in aggressive environments through multi-criteria group decision-making. DYNA, 98(5):477-483. DOI:10.6036/10816

Os paso el artículo en abierto, tanto en inglés como en español.

Descargar (PDF, 520KB)

Descargar (PDF, 390KB)

Evaluación de la capacidad de pensamiento crítico de los estudiantes universitarios en materia de sostenibilidad

Recientemente, hemos tenido el honor de que se publique nuestro artículo en el International Journal of Engineering Education, una revista indexada en el JCR. Nuestro estudio se enfoca en la evaluación de la capacidad de pensamiento crítico de los estudiantes universitarios en relación con la sostenibilidad. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal.

El artículo propone una metodología para evaluar objetivamente las habilidades de pensamiento crítico de los estudiantes universitarios en materia de sostenibilidad a través de estudios de casos que utilizan la técnica del Proceso de Jerarquía Analítica (AHP). La herramienta propuesta permite a los profesores identificar las áreas en las que los estudiantes carecen de una visión clara del problema y adaptar sus planes de estudio en consecuencia. El documento tiene como objetivo cerrar las brechas de conocimiento existentes en la evaluación de las competencias transversales que conducen a perfiles impulsores de los Objetivos de Desarrollo Sostenible (ODS).

Las implicaciones prácticas de este trabajo son las siguientes:

Los profesores pueden emplear la metodología propuesta para evaluar las habilidades de pensamiento crítico de sus alumnos en cursos relacionados con la sostenibilidad.
La herramienta puede ayudar a los profesores a identificar las áreas en las que los estudiantes carecen de una visión clara del problema y a adaptar sus planes de estudio en consecuencia.
La metodología propuesta se puede personalizar para cada disciplina universitaria para motivar a los estudiantes a través de estudios de casos reales y fomentar el pensamiento crítico y las habilidades analíticas desde el punto de vista de la sostenibilidad.
La metodología propuesta puede ayudar a cerrar las brechas de conocimiento existentes en la evaluación de las competencias transversales que conducen a perfiles impulsores de los Objetivos de Desarrollo Sostenible (ODS).

El artículo presenta los resultados de una encuesta realizada utilizando la metodología propuesta para evaluar las habilidades de pensamiento crítico de los estudiantes universitarios en materia de sostenibilidad a través de estudios de casos que utilizan la técnica del Proceso de Jerarquía Analítica (AHP). Se muestra la caracterización estadística de las respuestas dadas por los estudiantes, proporcionando el valor medio, la desviación estándar y los percentiles 5 y 95 de los juicios, medidos en términos de la escala fundamental extendida de Saaty. También se muestra la relevancia promedio asignada a cada criterio debido a esta encuesta. Estos valores de relevancia se obtienen de la metodología de toma de decisiones descrita anteriormente.

El artículo propone una metodología novedosa para evaluar la adquisición de habilidades de pensamiento crítico en materia de sostenibilidad por parte de los estudiantes universitarios. La metodología propuesta se basa en estudios de casos prácticos personalizados para cada disciplina universitaria, con el objetivo de motivar a los estudiantes a través de estudios de casos reales, así como fomentar el pensamiento crítico y las habilidades analíticas, todo ello desde el punto de vista de la sostenibilidad. La herramienta propuesta permite saber, a través de la coherencia de las respuestas de los estudiantes, en qué medida el estudiante ha desarrollado su capacidad de pensamiento crítico para enfrentar problemas de diseño sostenible. El artículo concluye que la metodología propuesta es útil para que los profesores adapten eficazmente sus planes de estudio de acuerdo con los conocimientos de sus alumnos.

ABSTRACT:

Construction-related enterprises are acknowledged as one of the key actors responsible for shifting society toward the sustainable future claimed by the recently established Sustainable Development Goals. However, university curricula need to emphasize guaranteeing the acquisition of transversal competencies that are essential for the future management professionals required by this new challenge. Consistent and critical thinking is considered a fundamental skill for education in sustainability. To date, no studies have presented an objective measure of the level of acquisition of such transverse skills in university curricula. This study provides an analytical tool to that end, based on the multi-criteria decision-making technique Analytic Hierarchy Process (AHP). Through sustainability-oriented case studies, students are faced with real managerial decision-making problems. The proposed method allows for the analytic quantification of the consistency of their responses. Such consistency is representative of their critical thinking skills. The proposed tool allows teachers not only to find the consistency of their students’ responses but also to understand in which areas of sustainability students lack a clear vision of the problem. This tool is therefore useful for teachers to effectively adapt their syllabi according to their students’ knowledge.

KEYWORDS:

Sustainable education; transversal competence; critical thinking; management; consistency

REFERENCE:

NAVARRO, I.J.; MARTÍ, J.V.; YEPES, V. (2023). Evaluation of Higher Education Students’ Critical Thinking Skills on Sustainability. International Journal of Engineering Education, 39(3):592-603.

Os paso el artículo, que está publicado en abierto. Espero que os sea de interés.

Descargar (PDF, 1.61MB)

Estudio de soluciones para el proyecto de una pasarela basado en un proceso analítico jerárquico

Durante los días 5-8 de julio de 2022 se celebró en Terrasa (Spain) el 26th International Congress on Project Management and Engineering AEIPRO 2022. Fue una buena oportunidad para debatir y conocer propuestas sobre dirección e ingeniería de proyectos. Nuestro grupo de investigación, dentro del proyecto de investigación HYDELIFE, presentó varias comunicaciones.

A continuación os paso una relacionada con el estudio de soluciones para el proyecto de una pasarela basado en un proceso analítico jerárquico (AHP).

Referencia:

YEPES-BELLVER, V.J.; ALCALÁ, J.; YEPES, V. (2022). Study of solutions for the design of a footbridge based on a hierarchical analytical process. 26th International Congress on Project Management and Engineering, AEIPRO, 5-8 de julio, Terrassa (Spain), pp. 512-524.

Os dejo un vídeo de la presentación realizada y la comunicación completa. Espero que os sean de interés.

Descargar (PDF, 1.16MB)

Ciclo de vida de puentes de hormigón en regiones costeras basada en el proceso analítico en red (ANP)

Acaban de publicarnos un artículo en Sustainability, revista indexada en el segundo cuartil del JCR. Se trata de aplicar la técnica de toma de decisiones en red ANP para evaluar la sostenibilidad del ciclo de vida de los puentes de hormigón en las regiones costeras. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València.

Desde que se establecieron los Objetivos de Desarrollo Sostenible en 2015, la evaluación de la sostenibilidad de las infraestructuras ha estado en el punto de mira de la comunidad científica. Esto se debe a que el sector de la construcción es esencial para promover el bienestar social y el desarrollo económico de los países, pero también es uno de los principales factores de estrés ambiental. Sin embargo, la evaluación de la sostenibilidad de las infraestructuras a lo largo de su ciclo de vida sigue siendo un reto importante, pues los criterios que intervienen en el diseño sostenible suelen ser complejos y contradictorios. El Proceso Analítico en Red (ANP) es una poderosa herramienta de toma de decisiones para modelar tales problemas. En este caso, se evalúa la sostenibilidad del ciclo de vida de diferentes alternativas de puentes de hormigón en ambiente costero utilizando el ANP. Los resultados obtenidos se comparan con los obtenidos mediante el Proceso Analítico Jerárquico (AHP) convencional. Los resultados obtenidos mediante ANP son más fiables que los derivados del AHP en términos de consistencia de los expertos y del número de comparaciones realizadas.

Abstract:

Since establishing the Sustainable Development Goals in 2015, the assessment of the sustainability performance of existing and future infrastructures has been in the spotlight of the scientific community. This is because the construction sector is essential for promoting the social welfare and economic development of countries, but is also one of the main environmental stressors existing to date. However, assessing infrastructure sustainability throughout its life cycle remains a significant challenge, as the criteria involved in sustainable design are often complex and conflicting. The Analytic Network Process (ANP) is recognized as a powerful decision-making tool to model such problems. Here, the life cycle sustainability performance of different design alternatives for a concrete bridge near the shore is evaluated using ANP. The obtained results are compared with those obtained using the conventional Analytical Hierarchy Process (AHP). The results obtained using ANP are more reliable than those derived from the conventional AHP in terms of the expert’s consistency and the number of comparisons made.

Keywords:

Sustainability; Analytic Network Process; bridge design; life cycle assessment; TOPSIS; multi-criteria decision making

Reference:

NAVARRO, I.J.; MARTÍ, J.V.; YEPES, V. (2022). Analytic Network Process-based sustainability life cycle assessment of concrete bridges in coastal regions. Sustainability, 14(17):10688. DOI:10.3390/su141710688

Como el artículo está publicado en abierto, os lo podéis descargar aquí mismo:

Descargar (PDF, 2.07MB)

Cálculo de la consistencia y el vector propio en AHP

En varios artículos de este blog hemos descrito distintos aspectos del Proceso Analítico Jerárquico (Analytic Hierarchy Process, AHP). Se trata de una técnica de decisión Multicriterio propuesta por T.L. Saaty que combina aspectos tangibles e intangibles para obtener, en una escala de razón, las prioridades asociadas con las alternativas del problema. No obstante, AHP presenta limitaciones que debemos conocer antes de utilizar este método.

Pues bien, una de las ventajas de AHP es que permite medir la consistencia del decisor al emitir sus juicios. Este aspecto es muy relevante, puesto que si decimos que A>B y que B>C, no podemos decir que A<C. Este aspecto es de gran interés cuando consultamos a expertos en una materia para comprobar que la información que nos facilita es correcta. Si la consistencia es aceptable, se puede continuar con el proceso de decisión. Pero si no lo es, entonces el que toma las decisiones debe replantearse sus juicios sobre las comparaciones pareadas antes de continuar con el análisis.

Saaty sugiere para el método AHP convencional (en el que se utiliza el método del autovector principal para obtener las prioridades), que la inconsistencia sea capturada mediante un único valor denominado índice de consistencia (Consistency Index, CI) donde λmax es el máximo autovalor y n es la dimensión de la matriz de decisión. Un índice de consistencia igual a cero significa que la consistencia es completa. Como esta medida depende del orden de la matriz (n), Saaty propone la utilización de la Razón de Consistencia (CR) que se obtiene dividiendo CI por su valor esperado RI, calculado a partir de un gran número de matrices recíprocas positivas de orden n generadas aleatoriamente (Tabla 1). Por tanto, una vez la matriz es consistente siempre y cuando CR no supere los valores indicados en la Tabla 2. Si en una matriz se supera el CR máximo, hay que revisar las ponderaciones.

Donde RI es el índice aleatorio, que indica la consistencia de una matriz aleatoria (Tabla 1):

Tabla 2. Porcentajes máximos del ratio de consistencia CR

Una vez verificada la consistencia, se obtienen los pesos, que representan la importancia relativa de cada criterio o las prioridades de las diferentes alternativas respecto a un determinado criterio. Para ello, el AHP original utiliza el método del autovector principal por la derecha, basado en el teorema de Perron-Frobenius, donde hay que resolver la siguiente ecuación:

donde A representa la matriz de comparación, w el autovector o vector de preferencia, y λmax el autovalor.

En la práctica, el vector de los pesos w=(w₁, w₂,…, w_n) se obtiene (método de las potencias) elevando la matriz de juicios a una potencia suficientemente grande, sumando por filas y normalizando estos valores mediante la división de la suma de cada fila por la suma total. El proceso concluye cuando la diferencia entre dos potencias consecutivas sea pequeña.

Sin embargo, este vector de los pesos de cada alternativa también se pueden calcular por el método de la media geométrica por filas (Crawford y Williams, 1985). En este caso, el peso de cada prioridad se calcula como la media geométrica por filas normalizado a la suma de las medias geométricas de todas las filas. Este método se está utilizando ampliamente en los últimos años por sus propiedades matemáticas y sociológicas. Los resultados de este método, comparados con el cálculo del autovector, son parecidos, aunque su cálculo es más sencillo.

De todas formas, os dejo un vídeo del profesor Aznar donde se explica con cierto detalle cómo calcular la consistencia y el autovector. Espero que os sea de utilidad.

Referencias:

AZNAR, J.; GUIJARRO, F. (2012). Nuevos métodos de valoración: modelos multicriterio. Editorial Universitat Politècnica de València.

CRAWFORD, G.; WILLIAMS, C. (1985). A note on the analysis of subjective judgement matrices. Journal of Mathematical Psychology, 29:387-405.

SAATY, T.L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Comparación pareada como método de evaluación de competencias transversales en materia de sostenibilidad

La evaluación de las competencias transversales adquiridas a lo largo de la formación universitaria es un objetivo fundamental para garantizar la adecuada formación de los alumnos. Con los recientemente establecidos Objetivos de Desarrollo Sostenible, la demanda de competencias transversales orientadas a tal fin es cada vez mayor y, su desarrollo y evaluación, más urgente. En el contexto de la sostenibilidad, resulta particularmente relevante la capacidad de pensamiento crítico de los estudiantes. Ante la falta de consenso en cuanto a cómo determinar el grado de adquisición de las competencias transversales, se propone un procedimiento objetivo orientado a la evaluación del pensamiento crítico basado en la resolución de casos de estudio, combinados con la aplicación del Proceso Analítico Jerárquico de decisión multicriterio. La aplicación de este proceso permite determinar, de forma objetiva, la coherencia implícita de los alumnos en sus juicios y ofrece, por lo tanto, una herramienta valiosa para evaluar su capacidad de pensamiento crítico y la claridad con la que perciben la sostenibilidad y sus implicaciones en el desarrollo de su futura práctica profesional.

Referencias:

NAVARRO, I.J.; YEPES, V.; MARTÍ, J.V. (2020). Comparación pareada como método de evaluación de competencias transversales en materia de sostenibilidad. VI Congreso de Innovación Educativa y Docencia en Red. IN-RED 2020, 16 y 17 de julio de 2020. Doi: http://dx.doi.org/10.4995/INRED2020.2020.12000

Descargar (PDF, 1.34MB)

Lógica neutrosófica aplicada al análisis de la sostenibilidad de puentes en ambientes marinos

Acaban de publicarnos un artículo en la revista Structure and Infrastructure Engineering (revista indexada en el JCR) sobre la aplicación de la lógica neutrosófica (una generalización de la lógica difusa y la lógica intuicionista) al diseño y mantenimiento de puentes en ambiente marino. El trabajo se enmarca dentro del proyecto de investigación DIMALIFE que dirijo como investigador principal en la Universitat Politècnica de València.

La metodología propuesta utiliza la lógica neutrosófica para obtener los pesos en un Proceso Analítico Jerárquico (AHP) que considerar la subjetividad de los expertos en el proceso de toma de decisión. Se ha aplicado al diseño sostenible de puentes y su mantenimiento considerando simultáneamente las tres dimensiones de la sostenibilidad.

El artículo se puede descargar gratuitamente en el siguiente enlace:

https://www.tandfonline.com/eprint/2KZDAHNK4BPJKPSY4XSF/full?target=10.1080/15732479.2019.1676791

ABSTRACT:

Essential infrastructures such as bridges are designed to provide a long-lasting and intergenerational functionality. In those cases, sustainability becomes of paramount importance when the infrastructure is exposed to aggressive environments, which can jeopardise their durability and lead to significant maintenance demands. The assessment of sustainability is however often complex and uncertain. The present study assesses the sustainability performance of 16 alternative designs of a concrete bridge deck in a coastal environment on the basis of a neutrosophic group analytic hierarchy process (AHP). The use of neutrosophic logic in the field of multi-criteria decision-making, as a generalisation of the widely used fuzzy logic, allows for a proper capture of the vagueness and uncertainties of the judgements emitted by the decision-makers. TOPSIS technique is then used to aggregate the different sustainability criteria. From the results, it is derived that only the simultaneous consideration of the economic, environmental and social life cycle impacts of a design shall lead to adequate sustainable designs. Choices made based on the optimality of a design in only some of the sustainability pillars will lead to erroneous conclusions. The use of concrete with silica fume has resulted in a sustainability performance of 46.3% better than conventional concrete designs.

Keywords: Sustainable design, chloride corrosion, neutrosophic sets theory, analytic hierarchy process, preventive maintenance, multi-criteria decision-making, life cycle assessment

REFERENCIA:

NAVARRO, I.J.; YEPES, V.; MARTÍ, J.V. (2020). Sustainability assessment of concrete bridge deck designs in coastal environments using neutrosophic criteria weights. Structure and Infrastructure Engineering, 16(7): 949-967. DOI:10.1080/15732479.2019.1676791

Proceso Analítico Jerárquico (Analytic Hierarchy Process, AHP)

En numerosas ocasiones contamos con muy poca información o tenemos que tomar una decisión teniendo en cuenta aspectos cualitativos que son difíciles de valorar. Para solucionar este tipo de problemas, muy habituales en situaciones reales, el profesor Thomas L. Saaty propuso en la década de los 70 un método denominado Analytic Hierarchy Process (AHP), que se ha traducido al español como Proceso Analítico Jerárquico. Este método multiatributo, nacido como respuesta a problemas concretos de toma de decisiones en el Departamento de Defensa de los Estados Unidos, hoy día se aplica habitualmente a casi todos los ámbitos de la empresa, la economía o la investigación de operaciones, entre otros muchos.

En apretada síntesis, AHP es un método que selecciona alternativas en función de una serie de criterios o variables, normalmente jerarquizados, los cuales suelen entrar en conflicto. En esta estructura jerárquica, el objetivo final se encuentra en el nivel más elevado, y los criterios y subcriterios en los niveles inferiores, tal y como se muestra en la Figura 2. Para que el método sea eficaz, es fundamental elegir bien los criterios y subcriterios, los cuales deben estar muy bien definidos, ser relevantes y mutuamente excluyentes (independencia entre ellos). Es importante que el número de criterios y subcriterios en cada nivel no sea superior a 7, para evitar excesivas comparaciones a pares.

Figura 2. Ejemplo de estructura jerárquica AHP

Una vez definida la estructura jerárquica, se comparan los criterios de cada grupo del mismo nivel jerárquico y la comparación directa por pares de las alternativas respecto a los criterios del nivel inferior. Para ello se utilizan matrices de comparación pareadas usando una Escala Fundamental (Tabla 1). Esta es la clave del método, usar una escala de comparación por pares, puesto que el cerebro humano está especialmente bien diseñado para comparar dos criterios o alternativas entre sí, pero menos cuando tiene que hacer comparaciones conjuntas. En efecto, la Ley de Weber-Fechner establece que el menor cambio discernible en la magnitud de un estímulo es proporcional a la magnitud de dicho estímulo. Como la relación entre el estímulo y la percepción corresponde a una escala logarítmica, si un estímulo crece en progresión geométrica, la percepción evolucionará como una progresión aritmética. Es por ello que AHP utiliza una escala fundamental del 1 al 9 que ha sido satisfactoria en comprobaciones empíricas realizadas en situaciones reales muy diversas.

Tabla 1. Escala fundamental de comparación por pares (Saaty, 1980)

La comparación de las diferentes alternativas respecto al criterio del nivel inferior de la estructura jerárquica, como la comparación de los diferentes criterios de un mismo nivel jerárquico dan lugar a una matriz cuadrada denominada matriz de decisión. Esta matriz cumple con las propiedades de reciprocidad (si aij=x, entonces aji=1/x), homogeneidad (si i y j son igualmente importantes, aij=aji=1, y además, aii= 1 para todo i), y consistencia (la matriz no debe contener contradicciones en la valoración realizada). La consistencia se obtiene mediante el índice de consistencia (Consistency Index, CI) donde λmax es el máximo autovalor y n es la dimensión de la matriz de decisión. Un índice de consistencia igual a cero significa que la consistencia es completa. Una vez obtenido CI, se obtiene la proporción de consistencia (Consistency Ratio, CR) siendo aceptado siempre que no supere los valores indicados en la Tabla 3. Si en una matriz se supera el CR máximo, hay que revisar las ponderaciones.

Donde RI es el índice aleatorio, que indica la consistencia de una matriz aleatoria (Tabla 2):

Tabla 3. Porcentajes máximos del ratio de consistencia CR

Una vez verificada la consistencia, se obtienen los pesos, que representan la importancia relativa de cada criterio o las prioridades de las diferentes alternativas respecto a un determinado criterio. Para ello, el AHP original utiliza el método de los autovalores, donde hay que resolver la siguiente ecuación:

donde A representa la matriz de comparación, w el autovector o vector de preferencia, y λmax el autovalor.

A continuación os dejo algunos vídeos de interés donde se explica el método AHP y sus aplicaciones. Espero que os sean de utilidad.

Referencias:

Saaty, T.L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation, McGraw-Hill.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Introducción a la toma de decisiones

Figura 1. De Lou Sander – Trabajo propio, Dominio público, https://commons.wikimedia.org/w/index.php?curid=8040446

Con esta entrada voy a iniciar una serie relacionada con la toma de decisiones. Todos tomamos decisiones a cada momento. Qué hago este fin de semana, si voy a ir al gimnasio dos o tres veces a la semana, a qué hora pongo el despertador, etc. Pues este tipo de decisiones no solo son individuales, sino que las empresas, los políticos o cualquier tipo de organización la deben tomar a cada momento. En la Figura 1 tenemos un ejemplo habitual: seleccionar un líder entre tres candidatos, tomando como criterios, por ejemplo, la edad, la experiencia, la educación o el carisma. Y muchas influyen significativamente en nuestra calidad de vida, en nuestras finanzas o en nuestro futuro. Es por esto, que la toma de decisiones se ha convertido en un proceso de gran importancia al que hay que prestar atención cuando se va a realizar la elección de una solución o alternativa.

Por cierto, si alguno está interesado en este tema y quiere participar en un número especial de la revista “Mathematics” sobre “Optimization for Decision Making” que estoy coordinando junto con el profesor José María Moreno, podéis acudir al siguiente enlace: http://victoryepes.blogs.upv.es/2018/10/11/special-issue-optimization-for-decision-making/?fbclid=IwAR3im1Wk2al8T6Rxstl6yWjOIaZvRtOpyIlQiYlT-Mr6ykF3QAXR5hVNbSI

Gran parte de las decisiones que tomamos en la vida diaria la realizamos intuitivamente. Sin embargo, cuando se presenta un problema de mayor importancia y se quiere convertir la toma de decisiones en un problema racional aparece el proceso de toma de decisiones (Figura 2), el cual está comprendido por 5 fases: (1) definición del problema, (2) identificación de las alternativas, (3) determinación de los criterios, (4) evaluación de las alternativas, y (5) elección de una opción.

Cuando la toma de una decisión depende de únicamente un único criterio, la solución óptima es aquella que optimiza dicho criterio. Este tipo de problema ofrece una visión parcial de la realidad, pues normalmente en la solución a un problema influyen numerosos aspectos que pueden ser contradictorios y entrar en conflicto entre sí. Aquí es donde entran en escena los problemas de decisión que tienen en cuenta dos o más criterios.

La toma de decisiones multicriterio constituye el proceso o acción que se utiliza para resolver un problema cuando son diferentes los criterios que deben considerarse. Por lo tanto, su objetivo principal es la evaluación de una serie de soluciones o alternativas Aj (i=1,2,…,n) a un problema basadas en las puntuaciones rij en relación a una serie de criterios Ci (j=1,2,…,m). La interacción entre los dos conjuntos de elementos se suele expresar como la matriz de toma de decisiones Mmn:

Las puntuaciones rij varían dependiendo de si el criterio evaluado es cuantitativo o cualitativo. Los criterios cuantitativos son criterios objetivos que se evalúan numéricamente, pero al tratar de realizar el mismo tipo de evaluación frente a criterios subjetivos, como son los cualitativos, la confusión aflora y se vuelve difícil asignar un valor numérico a un criterio cualitativo. Teniendo presente lo dicho, es más sencillo crear una escala de evaluación mediante términos lingüísticos que posteriormente sean asociados a valores numéricos. Un ejemplo será la utilización del Proceso Analítico Jerárquico (AHP), del cual hablaremos en su momento.

Por tanto, los criterios a evaluar pueden ser cuantitativos y cualitativos, y además dentro de cada grupo las unidades de medida pueden ser diferentes. Es por esto, que es necesario normalizar la matriz de toma de decisiones antes de evaluar las alternativas, de forma que las puntuaciones rij se conviertan en puntuaciones r’ij normalizadas. Paralelamente a la normalización de la matriz de toma de decisiones se deben obtener los pesos wi de cada criterio Ci en función de su importancia en la obtención de la meta final. Por lo tanto, la matriz de decisiones previa a la evaluación, se convierte en una matriz donde las puntuaciones rij se convierten en puntuaciones normalizadas con pesos asociados vij:

Los pesos asociados a cada criterio expresan la importancia relativa de cada uno de estos criterios, que sirven para alcanzar la valoración final de cada alternativa. La asignación de los pesos a cada criterio es un punto muy importante en la toma de decisiones, pues una pequeña variación de los mismos puede provocar que en un mismo problema, la solución final se decante por una u otra alternativa. Existe una gran variedad de métodos de asignación de pesos, que pueden considerarse objetivos o subjetivos. Pero eso lo dejamos para una entrada posterior.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.