El programa de la asignatura “Modelos Predictivos y de Optimización de Estructuras de Hormigón” se ha diseñado basándose en el programa presentado en el departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil por parte de la unidad docente de “Procedimientos de Construcción y Gestión de Obras”, al que está adscrita en la actualidad la asignatura, y aprobado por el Consejo del Departamento. Las líneas maestras de los contenidos se definieron previamente en la Memoria de Verificación del título oficial de “Máster Universitario en Ingeniería del Hormigón por la Universitat Politècnica de València”. Se trata de una de las asignaturas de la materia “Análisis de estructuras de hormigón”, siendo obligatoria para todos los alumnos de esta titulación y se imparte en el primer cuatrimestre del primer curso. La asignación de créditos ECTS es de 5,0, repartidos en 3,0 créditos de teoría y 2,0 de prácticas, de acuerdo con el Plan de Estudios actualmente en vigor en el Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil.
El programa de la asignatura “Modelos Predictivos y de Optimización de Estructuras de Hormigón” se ha diseñado basándose en el programa presentado en el departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil por parte de la unidad docente de “Procedimientos de Construcción y Gestión de Obras”, al que está adscrita en la actualidad la asignatura, y aprobado por el Consejo del Departamento. Las líneas maestras de los contenidos se definieron previamente en la Memoria de Verificación del título oficial de “Máster Universitario en Ingeniería del Hormigón por la Universitat Politècnica de València”. Se trata de una de las asignaturas de la materia “Análisis de estructuras de hormigón”, siendo obligatoria para todos los alumnos de esta titulación y se imparte en el primer cuatrimestre del primer curso. La asignación de créditos ECTS es de 5,0, repartidos en 3,0 créditos de teoría y 2,0 de prácticas, de acuerdo con el Plan de Estudios actualmente en vigor en el Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil.
Resultados de aprendizaje
Los resultados de aprendizaje de la asignatura se definen a partir de las competencias y de los contenidos (Yepes, 2017). Como resultado de aprendizaje general, al terminar con éxito esta asignatura, los estudiantes serán capaces de “comprender los diferentes métodos predictivos y procedimientos de optimización de estructuras de hormigón de modo que dispongan de las herramientas necesarias para la toma de decisiones en el ámbito del proyecto, construcción y mantenimiento de estas estructuras considerando los aspectos de sostenibilidad económica, social y ambiental”.
En relación con los resultados específicos de aprendizaje de la asignatura, tenemos los siguientes:
- RA1 Seleccionar y aplicar las distintas técnicas procedentes de la estadística, de la investigación operativa y de la minería de datos en la toma de decisiones en el ámbito del hormigón
- RA2 Modelizar un problema de optimización de una estructura de hormigón y resolverlo mediante algoritmos heurísticos secuenciales y poblacionales
- RA3 Aplicar la inferencia estadística multidimensional para interpretar el comportamiento de las variables cualitativas y cuantitativas en el ámbito del hormigón
- RA4 Formular modelos lineales de regresión múltiple e interpretar su validez límites predictivos
- RA5 Emplear técnicas de diseño de experimentos para conocer los efectos principales y las interacciones entre los distintos factores que afectan a una variable de respuesta en el ámbito del hormigón
- RA6 Optimizar el comportamiento de una estructura de hormigón utilizando la metodología de la superficie de respuesta
- RA7 Aplicar redes neuronales artificiales en la predicción de sistemas altamente no lineales en el ámbito del hormigón
- RA8 Aplicar técnicas de decisión multicriterio en la selección de la mejor tipología estructural considerando aspectos económicos, ambientales y sociales
- RA9 Elegir la mejor opción de una frontera de Pareto tras aplicar técnicas de decisión multicriterio
- RA10 Aplicar programas estadísticos avanzados, tales como SPSS o Minitab, y otros como Matlab, Sap y Excel en la predicción de variables de respuesta y en problemas de optimización en el ámbito del hormigón
Conocimientos previos
Los alumnos que cursan esta asignatura, tienen diversas procedencias: Ingeniería de Caminos, Canales y Puertos, Ingeniería Industrial, Arquitectura, Ingeniería Agronómica, Licenciado en Químicas, Ingeniería Geológica, Ingeniería Técnica de Obras Públicas, Ingeniería Técnica Industrial, o los actuales grados en ingeniería civil, de obras públicas o máster en ingeniería de caminos, canales y puertos, entre otros. Además los alumnos, en un porcentaje significativo, proceden de universidades latinoamericanas o europeas. Como es fácil de comprender, los alumnos tienen formaciones muy diferentes, habiendo estudiado las asignaturas relacionadas con el hormigón, con los métodos numéricos o la estadística de forma muy diversa, con niveles de adquisición de conocimientos descompensados. Esta situación implica cierta nivelación en cada uno de los temas, de forma que se adquieran los niveles básicos de comprensión de los contenidos de forma progresiva con el objetivo que todos los alumnos adquieran las competencias y los resultados de aprendizaje previstos.
Según la Guía Docente de la asignatura, los conocimientos recomendados versarían sobre estadística y sobre lenguajes de programación (MATLAB, SPSS, MINITAB, SAP, etc.), aunque no son imprescindibles. Además, resultan necesarios unos conocimientos básicos sobre el hormigón y su análisis como material estructural. Ello obliga al profesor a sintetizar el contenido previo para la correcta comprensión de la asignatura.
Programa resumido de la asignatura
La asignatura se desarrolla siguiendo un programa que tiene en cuenta los resultados de aprendizaje antes definidos, las actividades formativas y el sistema propuesto para la evaluación. Ello permite organizar la asignatura en 25 temas y sus prácticas de informática asociadas.
- Tema 1. La investigación operativa y la toma de decisiones
- Tema 2. La modelización de un problema estructural de hormigón
- Tema 3. Algoritmos y problemas de decisión
- Tema 4. Optimización y programación matemática
- Tema 5. Optimización combinatoria y algoritmos heurísticos
- Tema 6. Clasificación y uso de heurísticas y metaheurísticas
- Tema 7. Búsqueda local de máximo gradiente
- Tema 8. Recocido simulado, aceptación por umbrales y búsqueda tabú
- Tema 9. Sistemas de inteligencia de enjambre
- Tema 10. Programación evolutiva y estrategias evolutivas
- Tema 11. Algoritmos genéticos y meméticos
- Tema 12. GRASP, búsqueda dispersa y búsqueda de la armonía
- Tema 13. Heurísticas de optimización multiobjetivo
- Tema 14. Inferencia estadística bidimensional
- Tema 15. Inferencia estadística multidimensional
- Tema 16. Modelos lineales de regresión múltiple
- Tema 17. Modelos de ecuaciones estructurales
- Tema 18. Diseño de experimentos
- Tema 19. Optimización mediante la metodología de superficie de respuesta
- Tema 20. Modelos Kriging y diseños robustos
- Tema 21. Redes neuronales artificiales
- Tema 22. Programación genética y lógica difusa
- Tema 23. La toma de decisiones en el ciclo de vida de una estructura de hormigón
- Tema 24. Técnicas de decisión multicriterio continua
- Tema 25. Técnicas de decisión multicriterio discreta
Los 25 temas se encuentran agrupados en 4 bloques temáticos. El primero de los bloques es introductorio. Consta de 5 temas que presentan al alumno la aplicación de las técnicas de la investigación científica en el ámbito de la toma de decisiones en las empresas a través de lo que se conoce como investigación operativa. Se introduce al alumno en la forma de abordar los problemas reales en el ámbito de las estructuras de hormigón a través de modelos de distinto tipo. Se describen los componentes básicos de un problema de optimización: función objetivo, variables de decisión, parámetros y restricciones. A continuación se describe el concepto de algoritmo y complejidad algorítmica para explicar las limitaciones de la programación matemática en la resolución de problemas reales, lo cual da paso a la introducción de los algoritmos heurísticos como aproximaciones en la búsqueda de óptimos locales de calidad en tiempos de cálculo razonables.
El segundo de los bloques se centra en la descripción y aplicación de la optimización heurística en las estructuras de hormigón. Se describe paso a paso tanto las técnicas de búsqueda secuencial de máximo gradiente y de “hill-climbing” como otras técnicas poblacionales basadas en los algoritmos genéticos o en la inteligencia de partículas. Este bloque termina con una explicación de la optimización multiobjetivo y la construcción de fronteras de Pareto de calidad en el caso de confluencia de funciones objetivo contrapuestas.
El bloque tercero se centra específicamente en los modelos predictivos de las estructuras de hormigón. Se hace un repaso de las técnicas de inferencia bidimensional y multidimensional para pasar a los modelos predictivos lineales, tanto los basados en regresiones múltiples como en los modelos de ecuaciones estructurales. Posteriormente se aborda el diseño de experimentos como técnicas estadísticas básicas en la predicción de los efectos principales y las interacciones de los distintos factores que afectan a un problema de hormigón. El estudio de los diseños factoriales lleva directamente al planteamiento de la metodología de la superficie de respuesta, que permite realizar la optimización de la respuesta. Tanto la metodología de la superficie de respuesta como los modelos Kriging o las redes neuronales, constituyen metamodelos que se explican como herramientas muy útiles para simplificar el espacio de soluciones de los problemas reales del hormigón estructural. En particular, los modelos Kriging permiten el diseño robusto óptimo, es decir, aquel que se comporta bien incluso ante cambios en las variables o en las condiciones de contorno. Para los sistemas altamente complejos, se explican las redes neuronales artificiales que, además, permiten su uso como metamodelos o como parte de un algoritmo heurístico de optimización. La programación genética y la lógica difusa también se explican en una lección como herramientas posibles en el ámbito de los modelos predictivos y cuando los parámetros o restricciones del problema no son determinísticos.
El cuarto bloque se dedica a la toma de decisión multicriterio en las estructuras de hormigón. A los alumnos se les explica cómo, antes de realizar una optimización multiobjetivo, es necesario seleccionar la mejor tipología estructural con base en criterios que no siempre son objetivos: economía, plazo, estética, medioambiente, aspectos sociales, durabilidad, etc. Se introducen las distintas técnicas de toma de decisión multicriterio y se comentan su empleo, incluso, para la obtención de pesos objetivos de criterios que pueden ser incluso subjetivo, o bien para la selección de la mejor opción dentro de una frontera de Pareto tras una optimización multiobjetivo.
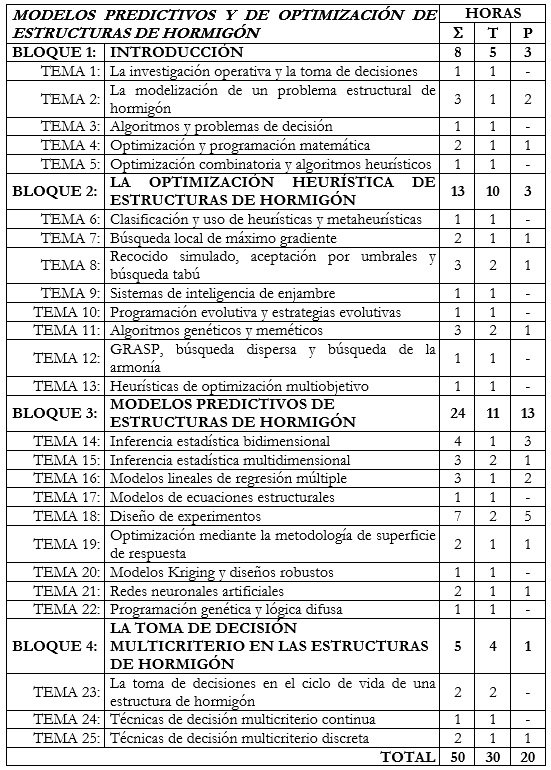
En la Tabla siguiente se muestra el programa resumido de la asignatura “Modelos Predictivos y de Optimización de Estructuras de Hormigón” (T, Teoría; P, Prácticas informáticas), indicándose el número de horas asignadas a cada tema.
Referencias:
YEPES, V. (2017). Proyecto docente. Concurso de Acceso al Cuerpo de Catedráticos de Universidad. Universitat Politècnica de València, 642 pp.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.