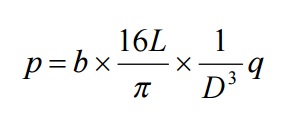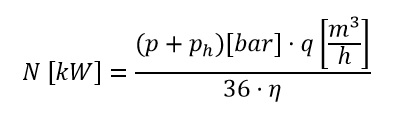bombeo del hormigón – El blog de Víctor Yepes

Maquinaria de bombeo de hormigón

Figura 1. Bomba sobre camión hormigonera Putzmeister.

En artículos anteriores ya comentamos aspectos sobre la colocación del hormigón mediante bombeo, así como del cálculo de la presión y potencia de bombeo. Ahora se trata de describir, muy brevemente, las máquinas de bombeo, impulsión y protección, que permiten colocar el hormigón en cualquier punto de la estructura, incluso en áreas difíciles o casi inaccesibles. Según su movilidad, se clasifican en estacionarias y móviles, y dentro de estas categorías, existen variantes según su uso.

Equipos estacionarios: Estas bombas se colocan al pie de obra y distribuyen el hormigón a través de tuberías presurizadas con aire comprimido y equipadas con cuatro gatos hidráulicos de estabilización que se fijan en el terreno. Su pluma de distribución es análoga a los móviles. Están montadas sobre un chasis de dos ruedas para facilitar su instalación y funcionamiento, y se fijan en su eje o sobre una bancada durante la operación. Además de bombear hormigón estructural, pueden utilizarse para proyectar enfoscados y hormigón de segunda capa, entre otros. Para usos temporales y cortos, suelen ser remolcadas. En este caso, se montan sobre un chasis de uno o dos ejes e incluyen pies estabilizadores.

Figura 2. Bomba estacionaria, con estabilizadores. https://www.maquinariacarran.cl/bomba-de-hormigon-cifa-pc307d/

Figura 3. Bomba estacionaria remolcada. https://www.sanyglobal.com/es_ar/bomba-estacionaria/HBT6006A-5.html

Equipos móviles o autobombas: Son bombas instaladas sobre el chasis de un camión, ya sea directamente mediante un bastidor que soporta todos los componentes necesarios para el bombeo, o a través de un semirremolque donde se monta dicho bastidor. Este bastidor incluye los elementos principales, como el grupo de bombeo, la pluma de distribución y los componentes auxiliares para su manejo: válvulas de seguridad, cuadro de control, palancas de accionamiento, telemando para controlar la pluma y zapatas estabilizadoras hidráulicas (4 o 6 unidades, en 2 o 3 ejes). También cuenta con un castillete giratorio que permite soportar y mover la pluma. Además, incorpora una tolva de recepción para recibir el hormigón que se va a bombear. Existen dos opciones para montar la autobomba: sobre un camión convencional o sobre un camión hormigonera. En este último caso, los componentes de la autobomba se adaptan al chasis del camión hormigonera y la tolva de recepción desaparece, ya que el grupo de bombeo toma el hormigón directamente de la cuba. Además, pueden bombear volúmenes de hasta 200 m³/h, aunque la capacidad promedio suele estar entre 40 y 60 m³/h. En el extremo del brazo se conecta una manguera flexible o con secciones troncocónicas conocidas como «trompa de elefante» que ayudan a mezclar nuevamente el hormigón fresco al pasar y evitan su segregación. Estas mangueras, fabricadas en PVC, permiten un vertido preciso, ya que son manejadas manualmente por el operario.

Los equipos de bombeo estacionarios, donde la mayoría son remolcados, poseen mayor potencia y presión máxima que las autobombas. A continuación, se puede ver un cuadro comparativo orientativo.

Tabla 1. Cuadro comparativo de distintos equipos de bombeo

Equipo de bombeo	Capacidad máxima (m³/h)	Presión de funcionamiento (kPa)
Móvil sobre hormigonera	60	6900
Móvil sobre camión	200	19500
Estacionario	200	24500

Tanto en los equipos móviles como en los estacionarios, la estructura presenta características similares, diferenciándose únicamente en su sistema de soporte. En los equipos móviles, esta estructura está montada sobre un camión, mientras que en los equipos estacionarios se utiliza principalmente una grúa torre o una columna tubular.

La estructura de los equipos, tanto móviles como estacionarios, se compone de tres o más brazos plegables hidráulicamente en el plano vertical, apoyados sobre un castillete cuya base incluye una corona de rodamientos de gran diámetro que permite el giro de la pluma en cualquier dirección mediante un motor hidráulico compensado. La altura de la pluma puede alcanzar hasta 60 m, siendo comúnmente de entre 20 y 35 m. En los equipos móviles, el castillete se ancla al bastidor auxiliar del chasis del camión, mientras que en los equipos estacionarios se emplean principalmente una torre o una columna tubular, esta última equipada con un sistema hidráulico que facilita el ascenso y el movimiento vertical de la pluma. En un artículo anterior se describió con mayor detalle las torres distribuidoras de hormigón (placing boom).

Figura 4. Características de una autobomba.

Os dejo a continuación una explicación al respecto de la UPV que espero que os sea de interés.

Os dejo algunos otros vídeos al respecto.

Referencias:

ACI COMMITTEE 304. Guide for Measuring, Mixing, Transporting, and Placing Concrete. ACI 304R-00.

BUSTILLO, M. (2008). Hormigones y morteros. Fueyo Editores, Madrid, 721 pp.

CALAVERA, J.et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

CORMON, P. (1979). Fabricación del hormigón. Editores Técnicos Asociados, Barcelona, 232 pp.

FERNÁNDEZ CÁNOVAS, M. (2004). Hormigón. 7ª edición, Colegio de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones, Madrid, 663 pp.

GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València.

MONTERO, E. (2006). Puesta en obra del hormigón. Exigencias básicas. Consejo General de la Arquitectura Técnica de España, Madrid, 750 pp.

MORILLA, I. (1992). Plantas de fabricación de hormigón y grava-cemento. Monografías de maquinaria. Asociación Española de la Carretera, Madrid.

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Cursos:

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Torres distribuidoras de hormigón: placing boom

Figura 1. Torre distribuidora de hormigón. https://socomaq.com/?product=placing-boom-truemax

Las torres distribuidoras de hormigón (TDH) o plumas de colocación estacionarias, también conocidas como placing boom, son brazos hidráulicos que complementan las bombas estacionarias, permitiendo una distribución eficiente del hormigón en elementos como losas, pilares o muros de edificios. Estas torres son un recurso clave para agilizar los procesos de hormigonado, ya que permiten distribuir el hormigón de manera independiente, tanto en elementos horizontales como verticales, sin depender de otros recursos esenciales en la obra, como la grúa pluma.

Los modelos más demandados cuentan con brazos de 28 y 32 m de longitud, lo que les permite colocar hormigón en superficies de 2810 y 3215 m², respectivamente, imitando de manera precisa el movimiento de una mano. Estas torres ahorran tiempo y dinero gracias a su fácil y rápida conversión de camión a torre, además de mejorar la seguridad en el trabajo y brindar mayor flexibilidad al contratista.

Entre sus principales ventajas se encuentran la velocidad de cobertura programable y la alta precisión en la colocación del hormigón, lo que reduce la necesidad de limpiar los encofrados y contribuye a prolongar su vida útil.

Estos equipos están formados por una columna que puede ascender a través de la estructura de hormigón armado mediante un sistema hidráulico de izaje autotrepatante. En la parte superior, el brazo articulado contiene una tubería interna que transporta el hormigón bombeado desde el nivel inferior hasta el distribuidor de hormigón.

Esta tecnología, combinada con una bomba de alimentación adecuada ubicada en la base del edificio, se presenta como una solución constructiva altamente eficiente. Permite la colocación de grandes volúmenes de hormigón, respondiendo de manera segura y rentable a las crecientes demandas de estructuras de gran altura, cada vez más complejas e innovadoras.

Figura 2. Placing boom. https://hormigonaldia.ich.cl/maquinarias/torres-de-distribucion-de-hormigon-rapidez-y-eficiencia-en-altura/

Os dejo algunos vídeos al respecto de este tipo de maquinaria de colocación del hormigón. Espero que os sean de interés.

Referencias:

ACI COMMITTEE 304. Guide for Measuring, Mixing, Transporting, and Placing Concrete. ACI 304R-00.

BUSTILLO, M. (2008). Hormigones y morteros. Fueyo Editores, Madrid, 721 pp.

CALAVERA, J.et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

CORMON, P. (1979). Fabricación del hormigón. Editores Técnicos Asociados, Barcelona, 232 pp.

FERNÁNDEZ CÁNOVAS, M. (2004). Hormigón. 7ª edición, Colegio de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones, Madrid, 663 pp.

GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón.Apuntes de la Universitat Politècnica de València.

MONTERO, E. (2006). Puesta en obra del hormigón. Exigencias básicas. Consejo General de la Arquitectura Técnica de España, Madrid, 750 pp.

MORILLA, I. (1992). Plantas de fabricación de hormigón y grava-cemento. Monografías de maquinaria. Asociación Española de la Carretera, Madrid.

Cursos:

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Nomogramas para el bombeo de hormigón

Roermond, the Netherlands, – August 08, 2019. Construction of a new highway tunnel in the center of the city.

En un artículo anterior explicamos cómo se podía calcular la presión y la potencia para el bombeo del hormigón. Aquí vamos a presentar un par de nomogramas que hemos desarrollado junto a los profesores Pedro Martínez Pagán y Daniel Boulet. Además, se incluye la resolución completa de un problema utilizando estos nomogramas.

Para los que estéis interesados en ampliar conocimientos, os recomiendo un libro de 300 problemas resueltos de Maquinaria y Procedimientos de Construcción. El libro ofrece una completa colección de 300 problemas resueltos, abarcando aspectos relacionados con la maquinaria, medios auxiliares y procedimientos de construcción. Su contenido se enfoca en la mecanización de las obras, costos, disponibilidad, fiabilidad y mantenimiento de equipos, estudio del trabajo, producción de maquinaria, sondeos y perforaciones, técnicas de mejora del terreno, control y abatimiento del nivel freático, movimiento de tierras, equipos de dragado, explosivos y voladuras, excavación de túneles, instalaciones de tratamiento de áridos, compactación de suelos, ejecución de firmes, maquinaria auxiliar como bombas, compresores o ventiladores, cables y equipos de elevación, cimentaciones y vaciados, encofrados y cimbras, fabricación y puesta en obra del hormigón, organización y planificación de obras. Es un libro, por tanto, muy enfocado a los ámbitos de la ingeniería de la construcción, tanto en el ámbito de la edificación, de la minería o de la ingeniería civil. Además, se incluyen 26 nomogramas originales y 19 apéndices para apoyar tanto a estudiantes de ingeniería o arquitectura, como a profesionales que enfrentan desafíos similares en su práctica diaria en obra o proyecto. La colección se complementa con un listado de referencias bibliográficas que respaldan los aspectos teóricos y prácticos abordados en los problemas. Estos problemas son similares a los tratados durante las clases de resolución de casos prácticos en la asignatura de Procedimientos de Construcción del Grado en Ingeniería Civil de la Universitat Politècnica de València (España). Por tanto, el libro resulta adecuado tanto para estudiantes de grado como para cursos de máster relacionados con la ingeniería civil, la edificación y las obras públicas.

Podéis conseguir el libro en el siguiente enlace: https://www.lalibreria.upv.es/portalEd/UpvGEStore/products/p_376-7-1

A continuación facilitamos un nomograma propio para el cálculo, que he elaborado junto con los profesores Martínez-Pagán y Boulet.

Os dejo un problema resuelto con estos nomogramas.

Descargar (PDF, 640KB)

Referencias:

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València.

RODRÍGUEZ-LÓPEZ, A.J. (2015). Determinación automática de la eficiencia volumétrica y otros parámetros de operación de bombas alternativas de hormigón mediante análisis de los pulsos de presión en su salida. Tesis doctoral. Universidad Politécnica de Madrid.

Cursos:

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Colocación del hormigón mediante bombeo

Figura 1. Bombeo de hormigón. https://www.balcellsintegralservice.com/bombeo-hormigon-barcelona-autobomba-sobre-camion.html

El bombeo del hormigón depende de la capacidad del equipo utilizado, del control y la homogeneidad de todos los ingredientes de la mezcla, de la dosificación y el mezclado, así como de los conocimientos y la experiencia del personal involucrado. La selección de equipos para el bombeo en condiciones óptimas depende de diversos factores específicos de cada obra. Para obtener información más detallada y concreta, se puede consultar la documentación técnica proporcionada por los fabricantes de bombas y las referencias bibliográficas disponibles. Se recomienda ponerse en contacto con el fabricante para determinar el tipo de bomba adecuado, pues los precios de alquiler aumentan en función de la capacidad del equipo. Es importante buscar una solución que sea razonable y eficiente.

Para que una operación de bombeo sea satisfactoria, es necesario un suministro constante de hormigón con las características adecuadas. Al igual que el hormigón convencional, requiere un buen control de calidad, una distribución homogénea de áridos, una granulometría adecuada y materiales dosificados y mezclados de manera uniforme. A continuación, se ofrecen algunas pautas generales sobre el proceso de bombeo de hormigón.

El proceso de colocación de hormigón por bombeo se basa en la bomba, la tubería y, en su caso, el sistema de distribución a la salida. La bomba debe estar diseñada para aspirar y empujar el volumen de hormigón requerido a través de la tubería hasta el punto de colocación. El tamaño máximo del árido viene determinado por los diámetros de los orificios de aspiración y de los cilindros de bombeo. Se recomienda que el diámetro del canal de aspiración sea al menos tres veces mayor que el tamaño máximo del árido.

Figura 2. Bomba de hormigón. https://ittcanarias.com/bombas-de-hormigon-putzmeister/

El tamaño máximo del árido grueso de forma angular se limita a un tercio del diámetro interior más pequeño de la tubería y, en el caso de áridos bien redondeados, debe ser inferior a dos quintos de este diámetro. El tamaño máximo del árido (TMA) influye significativamente en el volumen o cantidad de árido que puede utilizarse de manera eficiente. La cantidad de árido grueso debe reducirse considerablemente a medida que disminuye el TMA, pues la mayor superficie del árido de menor diámetro requiere más pasta para cubrir todas las superficies, lo que reduce la cantidad de pasta disponible para lubricar la línea de la tubería. Los áridos finos o arenas juegan un papel mucho más importante en la proporción de las mezclas bombeables que los áridos gruesos. Junto con el cemento y el agua, proporcionan el mortero que conduce en suspensión los sólidos o áridos gruesos, permitiendo así que una mezcla sea bombeable.

El uso de una autobomba suele estar limitado por una longitud máxima equivalente (L), calculada con la fórmula L = H + 3·V + 10·C₁ + 5·C₂, donde L debe ser menor o igual a 350 mm. En esta fórmula, H representa la distancia horizontal, V el desnivel vertical, C₁ el número de codos a 90º y C₂ el número de codos a 135º.

En el proceso de impulsión del hormigón, el parámetro principal es la máxima presión que puede generar la bomba. Generalmente, las autobombas utilizan una tubería corta que coincide con la longitud de la pluma de distribución, lo que implica que requieren una presión de bombeo menor en comparación con las bombas estacionarias. Estas últimas pueden bombear a distancias mayores con rendimientos similares. Por ejemplo, una presión de 7 MPa puede ser suficiente para las autobombas, incluso en casos de grandes caudales. Sin embargo, las bombas estacionarias necesitan alcanzar presiones de hasta 20 MPa para distancias horizontales de 1000 m o verticales de 500 m, lo que ilustra la diferencia en los requerimientos de presión entre ambos tipos de bombas.

La presión requerida para el bombeo varía en función de diversos factores, como la longitud, el diámetro y la cantidad de codos en la tubería, el caudal, la consistencia del hormigón y la altura. Los fabricantes de los equipos suelen proporcionar nomogramas que permiten estimar la presión necesaria para un caudal específico. En este enlace tenéis cómo realizar el cálculo de la presión y del caudal de bombeo.

Figura 3. Nomograma presión hormigón-rendimiento. Fuente: Bombas de hormigón estacionarias, Putzmeister

Durante el proceso de bombeo, el hormigón se transporta a través de tuberías metálicas de diversos espesores, diámetros, longitudes y sistemas de acoplamiento. Los diámetros de estas tuberías suelen oscilar entre 80 mm y 150 mm, con espesores habituales de entre 4 mm y 7 mm. La selección de estas variables está directamente relacionada con la presión de bombeo. Además, las longitudes típicas de los tramos individuales de tubería varían entre 1 m y 3 m.

La definición de los distintos aspectos geométricos de la tubería, junto con las características de su diseño en planta y alzado, es crítica para el proceso de bombeo. Además, el sentido del bombeo, ya sea ascendente o descendente, también es fundamental. Los sistemas de acoplamiento entre tramos individuales de tubería dependen de estas características geométricas del diseño.

Se recomienda ubicar la bomba lo más cerca posible de la zona de colocación del hormigón, utilizando una manguera flexible o un dispositivo articulado. En caso de emplear una tubería fija, se aconseja iniciar el hormigonado desde el punto más alejado de la bomba. Esto permite lubricar toda la tubería al principio y luego ir desmontando secciones de tubo y conectar la manguera de descarga en la parte final. Para este procedimiento, es necesario limpiar la tubería del hormigón utilizando agua o aire a presión.

Al poner en marcha los trabajos, se recomienda lubricar el interior de la tubería con una mezcla de mortero de cemento y arena. Una proporción de una parte de cemento por dos partes de arena es suficiente para lograr una consistencia fluida. Este mortero no solo lubrica la tubería, sino que también rellena posibles cavidades en las juntas del empalme. Aunque el método de lubricación con agua seguida por el paso de hormigón puede funcionar con dosificaciones especialmente diseñadas para el bombeo, existe el riesgo de obstrucciones en la tubería. En función de la naturaleza del material utilizado para la lubricación, este podrá emplearse o no en la colocación. Una vez que el flujo de hormigón comience a través de la tubería, la lubricación se mantendrá mientras el bombeo continúe con un diseño de mezcla adecuado y consistente.

Un problema habitual en el proceso de bombeo es la obstrucción del hormigón en la tubería. Por lo general, el operador de la bomba detecta la obstrucción al observar un aumento de la presión indicada. Los bloqueos pueden resolverse mediante ciclos que alteran la dirección de la presión, especialmente eficaces en conductos verticales. Sin embargo, este procedimiento no debe repetirse más de tres o cuatro veces. Si el bombeo no vuelve a la normalidad, es crucial identificar y eliminar la obstrucción en el punto donde se produjo.

Los atascos suelen ocurrir en el reductor a la salida de las válvulas y pueden detectarse cuando el manómetro registra una subida rápida de la presión. Cuando esto ocurre, es necesario desmontar y limpiar el reductor. No se debe forzar nunca la bomba y, si es preciso, se debe desmontar el tramo de conducción afectado. Si la presión no experimenta un aumento tan repentino, la obstrucción puede estar en el codo, el reductor o la manguera de descarga. Al observar la tubería e invertir la presión, se puede identificar la ubicación del atasco por las vibraciones que se producen. Normalmente, estos tapones no superan los 30 cm de longitud y se pueden desatascar desmontando un tramo de tubería.

Tabla 1. Localización de la obstrucción de una bomba

Subida de presión	Localización de la obstrucción
Brusca	Bomba o principio de la tubería
Lenta	Más alejado de la zona anterior (en la propia tubería)

Los conductos deben limpiarse al finalizar el trabajo o si hay una interrupción importante. El tiempo de espera no debe exceder media hora en climas cálidos y 1 hora en condiciones normales. La limpieza puede realizarse drenando el hormigón con agua o aire y, a continuación, bombeando una esponja húmeda en dirección opuesta para crear un vacío. Para limpiar las tuberías, existen dispositivos de limpieza de diversas rigideces que deben utilizarse con cuidado para evitar accidentes.

Al realizar un pedido de hormigón preparado a un proveedor y solicitar que sea bombeado, se debe proporcionar la siguiente información, además de la resistencia característica o la consistencia: especificar que el hormigón debe ser apto para el bombeo y las condiciones de especificación en la puesta en obra. También se debe informar sobre la cantidad y el caudal a bombear, la distancia en horizontal y vertical, el tiempo de funcionamiento de la bomba y los posibles tiempos de espera. Además, es importante indicar si se dispondrá de personal para ayudar en las operaciones de lubricación y limpieza de las tuberías.

Aquí tenéis algún vídeo ilustrativo del bombeo del hormigón.
https://www.youtube.com/watch?v=_VGtI5yHnx8https://www.youtube.com/watch?v=P3TLyBiuzcM

Os dejo un catálogo de bombas de hormigón estacionarias de la marca Liebherr, por si os resulta de interés.

Descargar (PDF, 3.64MB)

Y otro de la casa Putzmeister.

Descargar (PDF, 1.89MB)

Referencias:

AA. VV. (2002). Hormigones de ejecución especial (seis tipos). Colegio de Ingenieros de Caminos, Madrid, 114 pp.

ACI COMMITTEE 304. Placing Concrete by Pumping Methods (ACI 304.2R-17). American Concrete Institute.

CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València.

Cursos:

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Encofrados para hormigón autocompactante

Figura 1. Encofrado y colocación de hormigón autocompactante mediante bombeo tradicional. Fuente: https://www.ieca.es/wp-content/uploads/2017/10/Buron%20-%20Fernandez-Gomez%20-Garrido%20-%20autocompactante.pdf

El hormigón autocompactante (HCA) es aquel que se vierte en encofrados y se compacta únicamente por la acción de la gravedad, gracias a su capacidad innata de fluir. Esta técnica, lograda mediante una dosificación cuidadosa y el uso de aditivos superplastificantes específicos, permite que el hormigón se compacte uniformemente, eliminando huecos sin necesidad de vibración u otros métodos de compactación adicionales. Este enfoque mejora de manera notable la calidad, la durabilidad y la vida útil de las estructuras construidas con este material.

Sin embargo, para lograr los resultados deseados, es importante destacar que se requiere un encofrado robusto y perfectamente sellado para garantizar la estanqueidad del hormigón. Además, el encofrado debe estar dimensionado de acuerdo con las características del producto final, ya que el hormigón ejerce una presión hidrostática con un peso específico de 24 kN/m³.

El hormigón autocompactante fue concebido por Okamura en 1986 en Japón. Surgió con el objetivo de aumentar la productividad al reducir los tiempos de trabajo, de mejorar las condiciones ambientales en la obra y de superar desafíos estructurales emergentes, como la creación de formas y estructuras en las que la densidad de las armaduras dificulta el uso de métodos convencionales de compactación. Además, se buscaba mejorar las propiedades del producto final en términos de resistencia y durabilidad. Estas investigaciones condujeron al desarrollo del primer diseño de hormigón autocompactante en 1988.

En la actualidad, los fabricantes de encofrados han desarrollado elementos especiales para el hormigón autocompactante que incluyen una conexión para el conducto de la bomba y una trampilla de cierre. Estos elementos pueden instalarse tanto en el muro como en la parte frontal del elemento de encofrado, lo que garantiza un encofrado seguro en la parte inferior (Figura 2). Este procedimiento, en elementos de gran altura, evita la formación de burbujas de aire atrapadas entre la pared del encofrado y la masa de hormigón. Aunque, en todo caso, la formación de estas burbujas es mínima al emplear el desencofrante adecuado, es aún más reducida que en el caso del hormigón convencional. Se recomienda utilizar encofrados con cara metálica o superficies plastificadas no absorbentes para lograr texturas superficiales uniformes y minimizar la retención de burbujas de aire.

Figura 2. Conexión de la tubería de hormigonado por la parte inferior del encofrado. Fuente: https://www.proyectosyobrasmetrocubico.com/hormigon-autocompactante/

Dado que el hormigón se bombea desde la parte inferior del encofrado, se requieren pocos andamios, principalmente para controlar el proceso. Esta técnica de vertido garantiza que el encofrado permanezca limpio, tanto en su exterior como en las áreas no hormigonadas, lo que permite verter el hormigón incluso cuando la armadura es densa. Al bombear el hormigón desde abajo, no hay que preocuparse por la altura de caída libre del material. Sin embargo, si se optara por verter el hormigón directamente, es crucial evitar que caiga desde alturas superiores a los 2 m.

Dejo a continuación unos vídeos donde se realizan algunas consideraciones sobre los encofrados empleados en los hormigones autocompactantes. Espero que os sean de interés.

Dejo también un artículo sobre este tipo de hormigón, con sus características y puesta en obra.

Descargar (PDF, 2.42MB)

Referencias:

AFECI (2021). Guía sobre encofrados y cimbras. 3ª edición, Asociación de fabricantes de encofrados y cimbras, 76 pp.

ANDECE (2020). Guía técnica. Elementos prefabricados de hormigón para obras de ingeniería civil, 86 pp.

CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

PEURIFOY, R.L. (1967). Encofrados para estructuras de hormigón. McGraw-Hill y Ediciones Castillo, Madrid, 344 pp.

RICOUARD, M.J. (1980). Encofrados. Cálculo y aplicaciones en edificación y obras civiles. Editores Técnicos Asociados, S.A. Barcelona, 312 pp.

YEPES, V. (2024). Estructuras auxiliares en la construcción: Andamios, apeos, entibaciones, encofrados y cimbras. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 408 pp. Ref. 477. ISBN: 978-84-1396-238-2

Cursos:

Curso de estructuras auxiliares en la construcción: andamios, apeos, entibaciones, encofrados y cimbras.

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Cálculo de la presión y la potencia de bombeo del hormigón

https://pixabay.com/es/bomba-hormig%C3%B3n-m%C3%A1quina-construir-1902158/

La pérdida de carga en un circuito de transporte de hormigón (igual a la presión necesaria a la salida de la bomba) depende de una combinación de factores como son las propiedades del hormigón, el desnivel a salvar, la longitud del circuito, el caudal necesario, los diámetros de tubería y el material en que están construidas. El objetivo es encontrar una solución óptima, de modo que, por ejemplo, un menor diámetro equivale a un menor coste y menos desperdicio de mezcla durante la limpieza, pero requiere una presión de bombeo superior que, en algunos casos, puede ser inaceptable.

El hormigón fresco se comporta esencialmente como un fluido de Bingham y, por tanto, su flujo en tubería sigue la ley de Buckingham. Sin embargo, normalmente se acepta que existe una relación lineal entre la pérdida de carga y el caudal, en lugar de la relación cuadrática que establece la ecuación empírica de Darcy-Weisbach. Esta simplificación en el cálculo la asume el ACI (ACI 304.2r-96) y algunos fabricantes de bombas de hormigón (Putzmeister) al utilizar una fórmula empírica que indica que la relación presión-caudal (p–q) durante el bombeo es lineal, siendo el coeficiente de la ecuación que las vincula igual a una constante que depende de la geometría del circuito (cuantificada por su longitud L y diámetro D) y de las propiedades de la mezcla, expresadas en función de su asentamiento medido mediante el cono de Abrams a través del parámetro b.

Con las siguientes unidades: q (m³/h), L (m), D (m) y b (10^-6·bar·h/m), entonces p (bar). Además, b se puede obtener de la tabla siguiente en función del cono de Abrams:

Esta fórmula se ha utilizado ampliamente en la generación de ábacos o programas de cálculo de pérdidas de carga. Sin embargo, Putzmeister solo tabula el coeficiente b para valores de asentamiento menores de 12 cm, es decir, para hormigones relativamente consistentes, lo que deja fuera de su campo de aplicación a los hormigones fluidos. Si observamos, la pérdida de carga no depende de la presión existente en la tubería, hipótesis que algunos autores han comprobado. Esta aproximación empírica es útil desde el punto de vista práctico, pero no es satisfactoria desde un punto de vista teórico. Si bien proporciona buenos resultados en mezclas tradicionales, no resulta tan adecuada para los nuevos hormigones más fluidos como los autocompactantes o los de alta resistencia (Rodríguez López, 2015).

Para calcular la potencia de la bomba debemos considerar la presión originada por la pérdida de carga, más la presión necesaria para subir el hormigón a cierta altura. Dicha presión total se multiplicará por el caudal y se dividirá por el rendimiento η de la bomba para obtener la potencia N necesaria. La fórmula que hay que emplear es la siguiente:La presión en la conducción y la potencia de bombeo necesaria para transportar un determinado caudal de hormigón, puede calcularse por medio de ábacos como el de la figura en el que estos parámetros se relacionan con las características de la tubería y del hormigón de la siguiente forma: La escala vertical y horizontal del ábaco representa respectivamente en el caudal (m³/h) y la presión (bar) (en bombeo con altura de elevación, la presión total añadiendo a la presión indicada en el ábaco la presión en altura de la columna de hormigón). Además, en cada cuadrante figura el diámetro de la tubería, la longitud equivalente (longitud real + longitud añadida por pérdidas), la consistencia del hormigón y la potencia necesaria de la bomba. El resultado es aproximado y para un hormigón de buena dosificación. En este tipo de nomogramas se obtiene la potencia necesaria de la bomba, suponiendo un rendimiento de η=0,7. Este rendimiento puede caer a η=0,6 al sobrepasar los 50 bar.

Ejemplo: 40 m³/h de hormigón con un cono de Abrams de 60 mm deben bombearse a través de una tubería de 125 mm de diámetro a una distancia horizontal de 220 m y vertical de 73 m. Con el uso del nomograma de la Figura es fácil deducir la presión del hormigón y el rendimiento.

Fuente: Bombas de hormigón estacionarias, Putzmeister

Para elegir bien el equipo, debemos tener en cuenta algunos aspectos:

En primer lugar, debemos elegir el caudal de hormigón que vamos a bombear. Para ello, se parte del volumen de hormigón que se debe colocar y del tiempo del que se dispone. Además, hay que tener en cuenta que la bomba tiene tiempos muertos, por lo que es habitual suponer un rendimiento de 45 minutos por cada hora.
Para un caudal determinado, el diámetro de la tubería debe ser un compromiso entre los menores rozamientos, menor velocidad y mayor presión de los diámetros grandes, frente a la facilidad de montaje y de operaciones de bombeo de los diámetros menores.
Hay que calcular las pérdidas en la tubería que se añaden a la longitud real para calcular la longitud equivalente. Los codos de 30º, 60º y 90º equivalen a 1, 2 y 3 m de tubería. Si la manguera es flexible, la longitud hay que multiplicarla por 2. El conducto en vertical hay que multiplicarlo por 1,1.
No hay que olvidarse de sumar la presión necesaria para el bombeo en altura. En el caso de un peso específico del hormigón de 25 kN/m³, supone añadir 1 bar por cada 4 m de altura.

Descargar (PDF, 71KB)

Referencias:

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.