Este artículo describe la impartición de un curso de posgrado en el diseño automatizado y optimización económica de estructuras de hormigón. El contenido forma parte de un Máster en Ingeniería de Hormigón que comenzó en octubre de 2007. El curso aplica los algoritmos heurísticos al diseño práctico de estructuras reales de hormigón, tales como muros, pórticos y marcos de pasos inferiores de carreteras, pórticos de edificación, bóvedas, pilas, estribos y tableros de puentes. Se presentan como casos prácticos dos tableros de puente de hormigón pretensado usados en la obra pública de construcción de carreteras. En primer lugar, se aplica SA a un tablero de un puente peatonal de viga artesa de hormigón prefabricado. El segundo ejemplo aplica TA a un tablero de losa continua de hormigón postesado. Los casos estudiados indican que la optimización heurística es una buena opción para diseñar estructuras de hormigón pretensado reduciendo los costes.
Etiqueta: algoritmo
Optimización y programación matemática
Optimizar significa buscar la mejor manera de realizar una actividad, y en términos matemáticos, hallar el máximo o mínimo de una cierta función, definida en algún dominio. La optimización constituye un proceso para encontrar la mejor solución de un problema donde “lo mejor” se concilia con criterios establecidos previamente.
La programación matemática constituye un campo amplio de estudio que se ocupa de la teoría, aplicaciones y métodos computacionales para resolver los problemas de optimización condicionada. En estos modelos se busca el extremo de una función objetivo sometida a un conjunto de restricciones que deben cumplirse necesariamente. Las situaciones que pueden afrontarse con la programación matemática se suelen presentar en ingeniería, empresas comerciales y en ciencias sociales y físicas.
Con carácter general, un programa matemático (ver Minoux, 1986) consiste en un problema de optimización sujeto a restricciones en de la forma:
Teoría del valor extremo y optimización estructural
A continuación dejo una presentación que hicimos para el VII Congreso Español sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados MAEB 2010, que se celebró en Valencia del 8 al 10 de septiembre de 2010.
El artículo, denominado “Teoría del valor extremo como criterio de parada en la optimización heurística de bóvedas de hormigón estructural” establece un criterio de parada para un algoritmo multiarranque de búsqueda exhaustiva de máximo gradiente basado en una codificación Gray aplicado a la optimización de bóvedas de hormigón. Para ello se ha comprobado que los óptimos locales encontrados constituyen valores extremos que ajustan a una función Weibull de tres parámetros, siendo el de posición, γ, una estimación del óptimo global que puede alcanzar el algoritmo. Se puede estimar un intervalo de confianza para γ ajustando una distribución Weibull a muestras de óptimos locales extraídas mediante una técnica bootstrap de los óptimos disponibles. El algoritmo multiarranque se detendrá cuando se acote el intervalo de confianza y la diferencia entre el menor coste encontrado y el teórico ajustado a dicha función Weibull.
Referencia:
YEPES, V.; CARBONELL, A.; GONZÁLEZ-VIDOSA, F. (2010). Teoría del valor extremo como criterio de parada en la optimización heurística de bóvedas de hormigón estructural. Actas del VII Congreso Español sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados MAEB 2010, Valencia, 8-10 septiembre, pp. 553-560. Garceta Grupo Editorial. ISBN: 978-84-92812-58-5.
¿Cómo decidir cuando tenemos un dilema? El óptimo de Pareto
Los problemas de decisión están presentes en todos los ámbitos del ser humano: finanzas, empresa, ingeniería, salud, etc. Una de las grandes dificultades al tomar una decisión ocurre cuando queremos conseguir varios objetivos distintos, muchos de ellos incompatibles o contradictorios. Por ejemplo, si queremos un vehículo que sea muy veloz, debería tener un perfil aerodinámico que a veces es incompatible con la comodidad de los usuarios; si queremos hacer un negocio con grandes beneficios, a veces tenemos que asumir ciertos riesgos, etc. Una herramienta que permite afrontar este tipo de problemas de decisión es el denominado “óptimo de Pareto“. A continuación os paso un vídeo explicativo de este tema. Espero que os guste.
Introducción a la optimización heurística en ingeniería
Este pasado mes de octubre, estando como profesor visitante en la Universidad Católica de Chile, tuve la oportunidad de impartir un seminario introductorio a la optimización heurística en ingeniería. A continuación os paso la presentación. Espero que os guste.
¿Qué son las metaheurísticas?
¿Cómo se podrían optimizar en tiempos de cálculo razonable problemas complejos de redes de transporte, estructuras de hormigón (puentes, pórticos de edificación, túneles, etc.) y otro tipo de problemas de decisión empresarial cuando la dimensión del problema es de tal calibre que es imposible hacerlo con métodos matemáticos exactos? La respuesta son los métodos aproximados, también denominados heurísticas. Este artículo divulgativo trata de ampliar otros anteriores donde ya hablamos de los algoritmos, de la optimización combinatoria, de los modelos matemáticos y otros temas similares. Para más adelante explicaremos otros temas relacionados específicamente con aplicaciones a problemas reales. Aunque para los más curiosos, os paso en abierto, una publicación donde se han optimizado con éxito algunas estructuras de hormigón como muros, pórticos o marcos de carretera: (González et al, 2008).
Desde los primeros años de la década de los 80, la investigación de los problemas de optimización combinatoria se centra en el diseño de estrategias generales que sirvan para guiar a las heurísticas. Se les ha llamado metaheurísticas. Se trata de combinar inteligentemente diversas técnicas para explorar el espacio de soluciones. Osman y Kelly (1996) nos aportan la siguiente definición: “Los procedimientos metaheurísticos son una clase de métodos aproximados que están diseñados para resolver problemas difíciles de optimización combinatoria, en los que los heurísticos clásicos no son ni efectivos ni eficientes. Los metaheurísticos proporcionan un marco general para crear nuevos algoritmos híbridos combinando diferentes conceptos derivados de la inteligencia artificial, la evolución biológica y la mecánica estadística”.
Aunque existen diferencias apreciables entre los distintos métodos desarrollados hasta el momento, todos ellos tratan de conjugar en mayor o menor medida la intensificación en la búsqueda –seleccionando movimientos que mejoren la valoración de la función objetivo-, y la diversificación –aceptando aquellas otras soluciones que, aun siendo peores, permiten la evasión de los óptimos locales-.
Las metaheurísticas son susceptibles de agruparse de varias formas. Algunas clasificaciones recurren a cambios sucesivos de una solución a otra en la búsqueda del óptimo, mientras otras se sirven de los movimientos aplicados a toda una población de soluciones. El empleo, en su caso, de memoria que guíe de la exploración del espacio de elecciones posibles permite otro tipo de agrupamiento. En otras circunstancias se emplean perturbaciones de las opciones, de la topología del espacio de soluciones, o de la función objetivo. En la Figura se recoge una propuesta de clasificación de las heurísticas y metaheurísticas empleadas en la optimización combinatoria (Yepes, 2002), teniendo en común todas ellas la necesidad de contar con soluciones iniciales que permitan cambios para alcanzar otras mejores. Es evidente que existen en este momento muchas más técnicas de optimización, pero puede ser dicha clasificación un punto de partida para una mejor taxonomía de las mismas.
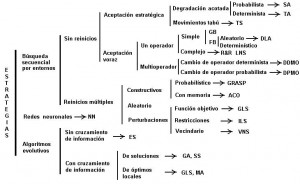
Las metaheurísticas empleadas en la optimización combinatoria en podrían clasificarse en tres grandes conjuntos. Las primeras generalizan la búsqueda secuencial por entornos de modo que, una vez se ha emprendido el proceso, se recorre una trayectoria de una solución a otra vecina hasta que éste concluye. En el segundo grupo se incluyen los procedimientos que actúan sobre poblaciones de soluciones, evolucionando hacia generaciones de mayor calidad. El tercero lo constituyen las redes neuronales artificiales. Esta clasificación sería insuficiente para aquellas metaheurísticas híbridas que emplean, en mayor o menor medida, estrategias de unos grupos y otros. Esta eventualidad genera un enriquecimiento deseable de posibilidades adaptables, en su caso, a los diferentes problemas de optimización combinatoria.
Referencias
GONZÁLEZ-VIDOSA-VIDOSA, F.; YEPES, V.; ALCALÁ, J.; CARRERA, M.; PEREA, C.; PAYÁ-ZAFORTEZA, I. (2008) Optimization of Reinforced Concrete Structures by Simulated Annealing. TAN, C.M. (ed): Simulated Annealing. I-Tech Education and Publishing, Vienna, pp. 307-320. (link)
OSMAN, I.H.; KELLY, J.P. (Eds.) (1996). Meta-Heuristics: Theory & Applications. Kluwer Academic Publishers.
YEPES, V. (2002). Optimización heurística económica aplicada a las redes de transporte del tipo VRPTW. Tesis Doctoral. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Universitat Politècnica de València. 352 pp. ISBN: 0-493-91360-2. (pdf)
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
Automatic design of concrete vaults using iterated local search and extreme value estimation
La optimización de estructuras reales de hormigón armado constituye un campo de gran interés no sólo en la investigación, sino en la aplicación real en obra. Os paso un artículo reciente donde se explica una forma de optimizar bóvedas de hormigón empleadas habitualmente en pasos inferiores como falsos túneles. Los ahorros que se pueden conseguir, en este caso, han sido de un 7% respecto a un diseño tradicional. En el caso de obras lineales de gran longitud, los ahorros pueden ser nada despreciables. La revista Latin American Journal of Solids and Structures es una revista en abierto, de donde podéis descargaros éste y otros artículos de interés.
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.
¿Qué es un algoritmo?
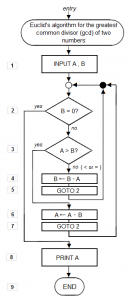
Un algoritmo es un conjunto prescrito de reglas o instrucciones bien definidas para la resolución de un problema. En general, se trata de encontrar el método más “eficiente”, no siendo baladí el modo de medir dicha eficiencia. Para resolver esta circunstancia, en la década de los 70 numerosos científicos se interesaron por la complejidad computacional de los problemas y los algoritmos. En muchos casos se asimila el rendimiento algorítmico a la medida del tiempo medio de ejecución empleado por un procedimiento para completar su operación con un conjunto de datos. Además, es posible relacionar el esfuerzo de cálculo con la dimensión del problema a resolver.
Un algoritmo muestra una complejidad polinómica si necesita un tiempo O(nk), donde n muestra la dimensión de entrada y k es una constante independiente de n. Si la función que denota la complejidad no está acotada por un polinomio, el algoritmo presenta una complejidad en tiempo exponencial.
Un problema de decisión es aquel que puede ser contestado con una afirmación o una negación. Llamemos P a la clase de problemas de decisión que pueden ser resueltos en tiempo cálculo que crece de forma polinomial ante incrementos lineales del número de elementos que intervienen, y NP aquellos solubles en un tiempo polinomial indeterminado, es decir, que se puede resolver en tiempo polinomial con una máquina Turing no determinística (ordenador). Un ordenador no determinístico puede ser contemplado como un autómata capaz de ejecutar un número ilimitado (pero finito) de ejecuciones en paralelo. Sólo los problemas en P son resolubles eficientemente mediante algoritmos, no conociéndose un procedimiento polinomial de resolución para los NP, siendo obvio que P pertenezca NP. Si lo contrario también ocurriera, P pertenecería a NP, querría decir que para la mayoría de los problemas de interés existen algoritmos eficientes que los resolvieran. Sin embargo, no se conoce la forma de demostrar que la igualdad P=NP sea cierta, ni tampoco que haya problemas en NP que no estén en P, es decir, la existencia de algún problema en NP que no se pueda resolver en tiempo polinómico (ver Díaz et al., 1996).
Un problema X se dice que es NP-completo (NPC) si cualquier problema en NP se puede transformar en X en tiempo polinomial. En este sentido, los NPC son una clase de problemas en NP muy difíciles. Si un solo problema en NPC se resolviera en tiempo polinomial, entonces todos los problemas NP también lo harían, lo cual no está demostrado a fecha de hoy. Sin embargo, no es necesario demostrar que un problema pertenece a NP para ofrecer evidencias de que es imposible resolverlo eficientemente. Sea Y un problema de decisión que no se conoce si es NP. Si un problema en NP-completo puede transformarse en Y, entonces Y no puede resolverse en tiempo polinomial (salvo que se demuestre que P=NP). Este problema Y sería como mínimo tan difícil como los NPC, llamándose NP-hard (NPH). Es decir, pueden existir problemas NPH que no sean NPC. A efectos prácticos únicamente nos interesa confirmar la NP-dificultad de un problema.
En la vida real existen numerosos problemas prácticos para los cuales se desconocen algoritmos eficientes (Yepes, 2002), pero cuya dificultad intrínseca no ha conseguido demostrar nadie. Es posible que existan realmente algoritmos eficientes, aunque también puede ocurrir que estos problemas sean intrínsecamente difíciles; no obstante, se carecen de las técnicas necesarias para demostrarlo. La importancia práctica de estos problemas ha asegurado que cada uno de ellos por separado haya sido objeto de esfuerzos sostenidos para hallar un método de solución eficiente. Por este motivo, se cree que no existen tales algoritmos. Como nadie, de momento, ha encontrado algoritmos eficientes para los problemas NP-completos, en cuanto se demuestra que un problema pertenece a esta clase, muchos investigadores tienden a pensar que no merece la pena buscar algoritmos eficientes para ellos. Lamentablemente, muchos de los problemas importantes que aparecen en Investigación Operativa son NP-completos. En Garey y Johnson (1979) se encuentra una visión más completa de la complejidad computacional.
REFERENCIAS
DÍAZ, A.; GLOVER, F.; GHAZIRI, H.M.; GONZÁLEZ, J.L.; LAGUNA, M.; MOSCATO, P.; TSENG, F.T. (1996). Optimización Heurística y Redes Neuronales en Dirección de Operaciones e Ingeniería. Paraninfo, Madrid. 235 pp.
GAREY, M.R.; JOHNSON, D.S. (1979). Computers and Intractability – A Guide to the Theory of NP-Completeness. W. H. Freeman and Company.
YEPES, V. (2002). Optimización heurística económica aplicada a las redes de transporte del tipo VRPTW. Tesis Doctoral. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos. Universitat Politècnica de València. 352 pp. ISBN: 0-493-91360-2. (pdf)
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.