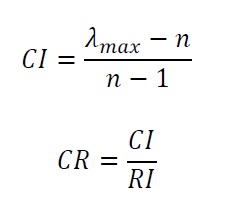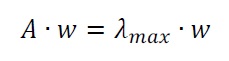AHP – El blog de Víctor Yepes

Métodos multicriterio: la clave para rehabilitar edificios vulnerables en zonas sísmicas

Un equipo de investigadores de la Universitat Politècnica de València y la Universidad Central del Ecuador ha llevado a cabo un análisis exhaustivo sobre los métodos de toma de decisiones multicriterio (MCDM) aplicados a la evaluación, selección y rehabilitación de edificios. Publicado en la prestigiosa revista Journal of Civil Engineering and Management, este artículo aborda una problemática clave en la ingeniería civil actual: cómo hacer frente al envejecimiento del parque de edificios, muchos de los cuales se construyeron siguiendo normativas de seguridad y sostenibilidad ya obsoletas.

La necesidad de abordar esta cuestión es urgente, dado que muchos edificios existentes no cumplen con los estándares actuales de seguridad, en particular respecto a su vulnerabilidad sísmica. Este factor es especialmente relevante en países con un alto riesgo, donde recientes terremotos han demostrado la fragilidad de las infraestructuras más antiguas. Además de las posibles pérdidas humanas, el impacto económico y social de estos eventos puede ser devastador.

Esta investigación es el resultado de una colaboración internacional realizada en el marco de los proyectos HYDELIFE y RESILIFE, cuyo investigador principal es Víctor Yepes, y es fruto de una colaboración internacional entre investigadores de Ecuador y España.

Contexto de la investigación

El envejecimiento del parque de edificios es un problema global que afecta tanto a países desarrollados como en vías de desarrollo. Muchos edificios antiguos se construyeron siguiendo normativas obsoletas que no tenían en cuenta los estándares de seguridad modernos, especialmente en lo que respecta al riesgo sísmico. A esto se suma la necesidad de hacer frente a desafíos medioambientales, como el impacto de la construcción en el consumo energético y las emisiones de CO₂. Ante esta situación, surge la necesidad de adoptar estrategias de rehabilitación que combinen la seguridad estructural con la sostenibilidad. La integración de factores sociales, económicos y ambientales en la toma de decisiones sobre la rehabilitación de edificios es fundamental para avanzar hacia un entorno construido más seguro y sostenible.

Metodología

La investigación se basa en una revisión bibliométrica de la literatura sobre los métodos MCDM aplicados a la evaluación y rehabilitación de edificios. Se analizaron 91 artículos publicados entre 2008 y 2023, utilizando bases de datos especializadas como Web of Science y SCOPUS. Los estudios seleccionados abordan tanto la evaluación de la vulnerabilidad de los edificios como la selección de estrategias de rehabilitación, con un enfoque particular en edificios escolares y patrimoniales, que suelen estar más expuestos a riesgos debido a su antigüedad o importancia cultural.

Se evaluaron las tendencias en el uso de los métodos MCDM y se identificaron investigaciones clave que han logrado evaluar de manera conjunta el consumo energético y la vulnerabilidad sísmica. Estas investigaciones destacan la necesidad de contar con metodologías que permitan evaluar múltiples factores de manera simultánea y en contextos de incertidumbre, especialmente cuando se trata de estructuras vulnerables, como las escuelas y los edificios patrimoniales, que requieren un enfoque especializado tanto por su valor cultural como por su complejidad estructural. Los investigadores clasificaron los diferentes métodos MCDM más utilizados, como el Proceso de Análisis Jerárquico (AHP), el Simple Additive Weighting (SAW) y el TOPSIS. Cada método se evaluó en función de su capacidad para integrar criterios contradictorios, como la seguridad estructural, el impacto económico, social y ambiental.

Resultados

El estudio revela la prevalencia de ciertos métodos clásicos en la investigación científica, como el ya mencionado AHP, que se ha combinado en muchos estudios con TOPSIS, un enfoque que permite identificar soluciones óptimas al considerar tanto la distancia a una solución ideal como a una no ideal. Este enfoque se ha aplicado tanto a la selección de edificios que requieren intervenciones urgentes como a la identificación de estrategias de rehabilitación más eficaces. Estos métodos permiten ponderar diversos criterios y encontrar soluciones que maximicen la seguridad y la sostenibilidad. Entre los principales hallazgos destacan:

Evaluación de la vulnerabilidad: Se ha aplicado MCDM para evaluar la vulnerabilidad de los edificios en zonas urbanas, con un enfoque particular en las escuelas y los edificios patrimoniales. En muchos casos, los estudios integraron criterios de vulnerabilidad sísmica con aspectos socioeconómicos y ambientales.
Selección de estrategias de rehabilitación: El estudio identificó tres enfoques principales en la rehabilitación de edificios: la intervención en componentes individuales, la adición de elementos de resistencia y la reducción de demandas estructurales mediante dispositivos suplementarios. La combinación de sostenibilidad y seguridad ha sido un aspecto clave en estos estudios.
Sostenibilidad: Si bien muchos estudios ya integran criterios de sostenibilidad, solo un porcentaje menor (15 %) incorpora análisis del ciclo de vida (LCA), una herramienta crucial para medir el impacto ambiental de las intervenciones a largo plazo.

Implicaciones

Las conclusiones de este trabajo tiene importantes implicaciones tanto para la práctica de la ingeniería civil como para las políticas públicas. La aplicación de métodos MCDM permite a los ingenieros y a los responsables de la toma de decisiones considerar una variedad de factores antes de seleccionar una estrategia de rehabilitación para un edificio. Esto es particularmente relevante en áreas con alto riesgo sísmico, donde la rehabilitación de edificios vulnerables puede salvar vidas y reducir las pérdidas económicas.

Además, la integración de criterios de sostenibilidad subraya la importancia de las políticas que promuevan rehabilitaciones que no solo refuercen la seguridad, sino que también reduzcan el impacto ambiental. Los resultados del estudio sugieren que las futuras investigaciones deberían centrarse en la creación de metodologías más avanzadas que manejen mejor la incertidumbre y que logren una verdadera integración de los pilares de sostenibilidad (económico, social y ambiental) con los criterios de seguridad estructural.

En resumen, este estudio ofrece una perspectiva innovadora sobre la forma en que los métodos MCDM pueden ayudar a afrontar los retos actuales en la rehabilitación de edificios. Su aplicación no solo mejora la seguridad de las infraestructuras, sino que también permite avanzar hacia un modelo de construcción más sostenible y eficiente. Sus recomendaciones son claras: es necesario seguir investigando para mejorar las soluciones de toma de decisiones que integren de manera efectiva la seguridad estructural y la sostenibilidad. Esto es fundamental no solo para garantizar la seguridad de los edificios, sino también para asegurar que las futuras generaciones puedan disfrutar de un entorno construido que sea resiliente, seguro y sostenible.

Referencia:

VILLALBA, P.; SÁNCHEZ-GARRIDO, A.; YEPES, V. (2024). A review of multi-criteria decision-making methods for building assessment, selection, and retrofit. Journal of Civil Engineering and Management, 30(5):465-480. DOI:10.3846/jcem.2024.21621

Este artículo está publicado en abierto, por lo que puedes descargar aquí mismo:

Descargar (PDF, 1.66MB)

Coste del ciclo de vida de las baterías de NiZn mediante Optimización Multiobjetivo por Enjambre de Partículas

Acaban de publicarnos un artículo en la revista Sustainability, revista indexada en el JCR. El artículo de investigación se centra en la optimización de las funciones de coste del ciclo de vida (LCC) e impacto ambiental (LCA) de las baterías de níquel-zinc (NiZn) mediante el algoritmo de optimización por enjambres de partículas multiobjetivo (MOPSO). El proceso de optimización se centra en las fases de adquisición de materias primas y de fin de vida útil de las baterías de NiZn para mejorar sus indicadores clave de rendimiento (KPI) de sostenibilidad. La metodología, implementada en MATLAB, utiliza un modelo de formulación de LCC y LCA ambiental, e incorpora datos de la base de datos Ecoinvent, el software OpenLCA y otras bases de datos públicas. Los resultados obtenidos gracias a la optimización proporcionan información sobre las combinaciones de países más eficaces para obtener materias primas para la producción de baterías de NiZn y gestionar los residuos de las baterías que no se pueden reciclar. Los KPI de sostenibilidad, como el impacto del calentamiento global y los costes de capital, se vinculan automáticamente a los resultados, lo que garantiza su reproducibilidad en caso de actualizaciones de datos o cambios en las ubicaciones de producción y reciclaje establecidas inicialmente en París (Francia) y Krefeld (Alemania). El proceso de validación implica un análisis de sensibilidad para garantizar la solidez de los parámetros matemáticos y tener en cuenta las futuras variaciones del mercado, junto con el uso del proceso jerárquico analítico (AHP) para validar los resultados con interacciones humanas. En el futuro, se sugiere incluir las fases de fabricación y uso en el modelo de optimización para mejorar aún más la sostenibilidad y la eficiencia de las baterías de NiZn.

Como conclusiones más importantes de este trabajo, se pueden señalar las siguientes:

El estudio optimizó el ciclo de vida, el impacto ambiental y el costr de las baterías de NiZn, utilizando los datos más recientes disponibles de los principales productores y centros de tratamiento de residuos.
La optimización por enjambres de partículas multiobjetivo (MOPSO) se consideró más adecuada que el algoritmo genético (GA) para la optimización multiobjetivo, debido a su eficiencia y eficacia.
El análisis tuvo en cuenta 14 flujos de materiales, una línea de eliminación de residuos y varias ubicaciones del mundo con diferentes costes e impactos ambientales, lo que puso de relieve la complejidad del proceso de optimización.
Mediante el MOPSO, se identificaron las ubicaciones óptimas de los proveedores de materias primas con un coste e impacto medioambiental mínimos, así como las ubicaciones de eliminación de residuos de materiales no reciclables.
Se recomendaron países proveedores óptimos específicos para los diferentes materiales, haciendo hincapié en la importancia de tomar decisiones estratégicas de abastecimiento para reducir el impacto ambiental y los costes.
El modelo de IA demostró su solidez al alinearse con los resultados del proceso jerárquico analítico (AHP) y mostrar su resiliencia a las fluctuaciones del mercado en el análisis de sensibilidad.
El estudio hizo hincapié en la necesidad de contar con módulos de programación dinámicos para estimar los indicadores clave de rendimiento (KPI) de sostenibilidad y validar los resultados de la optimización, especialmente en las fases de adquisición de materias primas y eliminación de residuos.
La validación mediante el AHP reveló similitudes y diferencias entre la IA y los resultados de las encuestas de un panel de expertos, lo que puso de manifiesto la eficacia del modelo de IA en la toma de decisiones estratégicas para el abastecimiento y la gestión de residuos.
El documento concluyó destacando la importancia de incorporar las fases de fabricación y uso en los futuros modelos de optimización para mejorar aún más la sostenibilidad y la eficiencia de las baterías de NiZn.

Abstract:

This study aims to optimize the Environmental Life Cycle Assessment (LCA) and Life Cycle Cost (LCC) of NiZn batteries using Pareto Optimization (PO) and Multi-objective Particle Swarm Optimization (MOPSO), which combine Pareto optimization and genetic algorithms (GA). The optimization focuses on the raw material acquisition and end-of-life phases of NiZn batteries to improve their sustainability Key Performance Indicators (KPIs). The optimization methodology, programmed in MATLAB, is based on a formulation model of LCC and the environmental LCA, using data from the Ecoinvent database, the OpenLCA software (V1.11.0), and other public databases. Results provide insights about the best combination of countries for acquiring raw materials to manufacture NiZn and for disposing of the waste of NiZn batteries that cannot be recycled. These results were automatically linked to some sustainability KPIs, such as global warming and capital costs, being replicable in case of data updates or changes in production or recycling locations, which were initially considered at Paris (France) and Krefeld (Germany), respectively. These results provided by an AI model were validated by using a sensitivity analysis and the Analytical Hierarchy Process (AHP) through an expert panel. The sensitivity analysis ensures the robustness of mathematical parameters and future variations in the market; on the other hand, the AHP validates the Artificial Intelligence (AI) results with interactions of human factors. Further developments should also consider the manufacturing and use phases in the optimization model.

Keywords:

LCCA; LCA; MOPSO; genetic algorithms; AHP; sustainability KPIs; AI; NiZn batteries

Reference:

MALVIYA, A.K.; ZAREHPARAST MALEKZADEH, M.; SANTARREMIGIA, F.E.; MOLERO, G.D.; VILLALBA-SANCHIS, I.; MARTÍNEZ-FERNÁNDEZ, P.; YEPES, V. (2024). Optimization of the Life cycle cost and environmental impact functions of NiZn batteries by using Multi-Objective Particle Swarm Optimization (MOPSO). Sustainability, 16(15):6425. DOI:10.3390/su16156425

Descargar (PDF, 2.03MB)

Evaluación de la capacidad de pensamiento crítico de los estudiantes universitarios en materia de sostenibilidad

Recientemente, hemos tenido el honor de que se publique nuestro artículo en el International Journal of Engineering Education, una revista indexada en el JCR. Nuestro estudio se enfoca en la evaluación de la capacidad de pensamiento crítico de los estudiantes universitarios en relación con la sostenibilidad. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal.

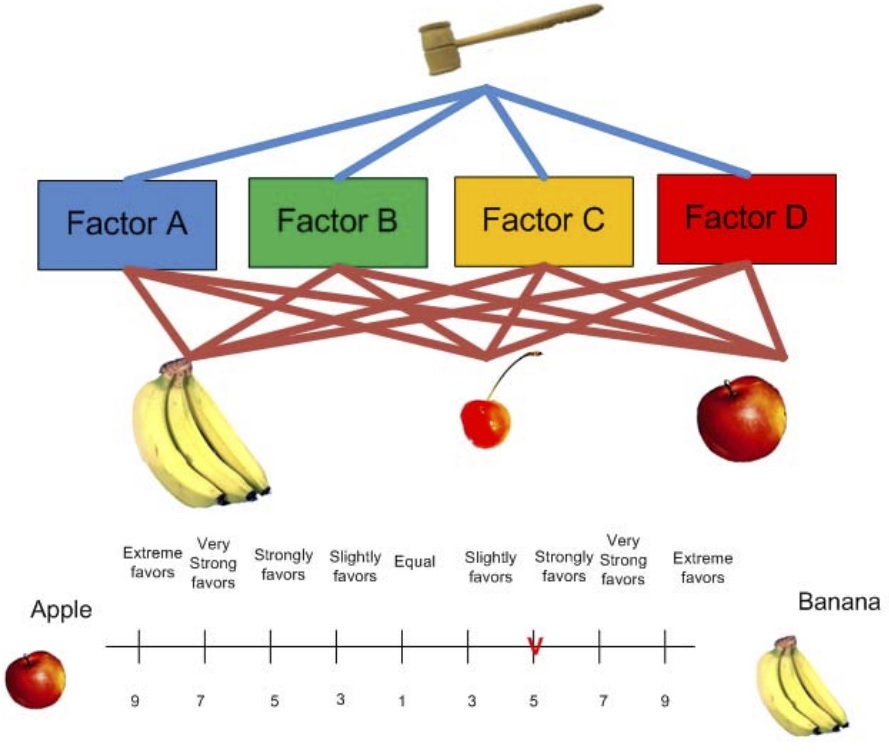
El artículo propone una metodología para evaluar objetivamente las habilidades de pensamiento crítico de los estudiantes universitarios en materia de sostenibilidad a través de estudios de casos que utilizan la técnica del Proceso de Jerarquía Analítica (AHP). La herramienta propuesta permite a los profesores identificar las áreas en las que los estudiantes carecen de una visión clara del problema y adaptar sus planes de estudio en consecuencia. El documento tiene como objetivo cerrar las brechas de conocimiento existentes en la evaluación de las competencias transversales que conducen a perfiles impulsores de los Objetivos de Desarrollo Sostenible (ODS).

Las implicaciones prácticas de este trabajo son las siguientes:

Los profesores pueden emplear la metodología propuesta para evaluar las habilidades de pensamiento crítico de sus alumnos en cursos relacionados con la sostenibilidad.
La herramienta puede ayudar a los profesores a identificar las áreas en las que los estudiantes carecen de una visión clara del problema y a adaptar sus planes de estudio en consecuencia.
La metodología propuesta se puede personalizar para cada disciplina universitaria para motivar a los estudiantes a través de estudios de casos reales y fomentar el pensamiento crítico y las habilidades analíticas desde el punto de vista de la sostenibilidad.
La metodología propuesta puede ayudar a cerrar las brechas de conocimiento existentes en la evaluación de las competencias transversales que conducen a perfiles impulsores de los Objetivos de Desarrollo Sostenible (ODS).

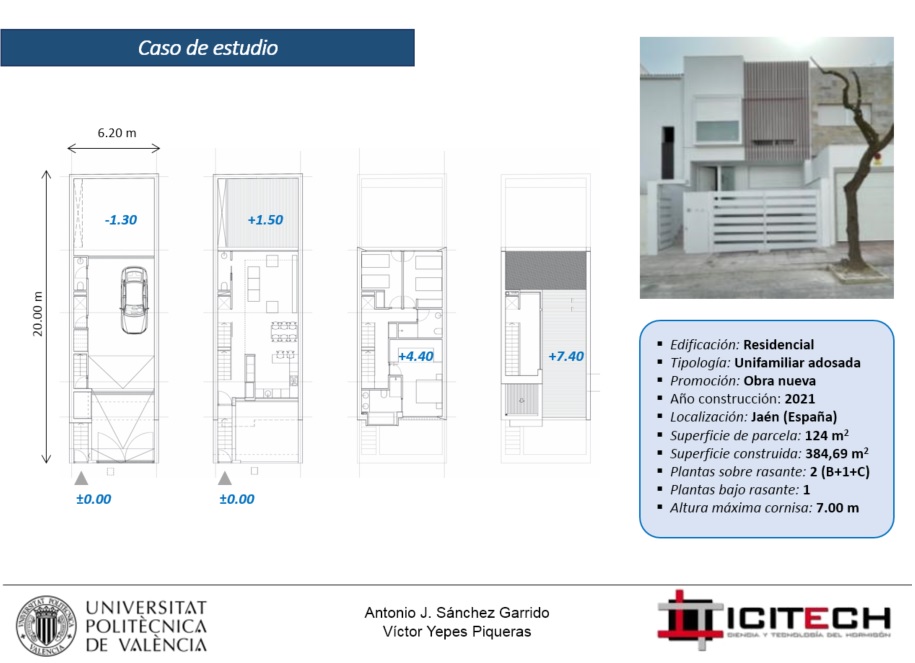
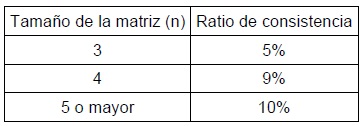
El artículo presenta los resultados de una encuesta realizada utilizando la metodología propuesta para evaluar las habilidades de pensamiento crítico de los estudiantes universitarios en materia de sostenibilidad a través de estudios de casos que utilizan la técnica del Proceso de Jerarquía Analítica (AHP). Se muestra la caracterización estadística de las respuestas dadas por los estudiantes, proporcionando el valor medio, la desviación estándar y los percentiles 5 y 95 de los juicios, medidos en términos de la escala fundamental extendida de Saaty. También se muestra la relevancia promedio asignada a cada criterio debido a esta encuesta. Estos valores de relevancia se obtienen de la metodología de toma de decisiones descrita anteriormente.

El artículo propone una metodología novedosa para evaluar la adquisición de habilidades de pensamiento crítico en materia de sostenibilidad por parte de los estudiantes universitarios. La metodología propuesta se basa en estudios de casos prácticos personalizados para cada disciplina universitaria, con el objetivo de motivar a los estudiantes a través de estudios de casos reales, así como fomentar el pensamiento crítico y las habilidades analíticas, todo ello desde el punto de vista de la sostenibilidad. La herramienta propuesta permite saber, a través de la coherencia de las respuestas de los estudiantes, en qué medida el estudiante ha desarrollado su capacidad de pensamiento crítico para enfrentar problemas de diseño sostenible. El artículo concluye que la metodología propuesta es útil para que los profesores adapten eficazmente sus planes de estudio de acuerdo con los conocimientos de sus alumnos.

ABSTRACT:

Construction-related enterprises are acknowledged as one of the key actors responsible for shifting society toward the sustainable future claimed by the recently established Sustainable Development Goals. However, university curricula need to emphasize guaranteeing the acquisition of transversal competencies that are essential for the future management professionals required by this new challenge. Consistent and critical thinking is considered a fundamental skill for education in sustainability. To date, no studies have presented an objective measure of the level of acquisition of such transverse skills in university curricula. This study provides an analytical tool to that end, based on the multi-criteria decision-making technique Analytic Hierarchy Process (AHP). Through sustainability-oriented case studies, students are faced with real managerial decision-making problems. The proposed method allows for the analytic quantification of the consistency of their responses. Such consistency is representative of their critical thinking skills. The proposed tool allows teachers not only to find the consistency of their students’ responses but also to understand in which areas of sustainability students lack a clear vision of the problem. This tool is therefore useful for teachers to effectively adapt their syllabi according to their students’ knowledge.

KEYWORDS:

Sustainable education; transversal competence; critical thinking; management; consistency

REFERENCE:

NAVARRO, I.J.; MARTÍ, J.V.; YEPES, V. (2023). Evaluation of Higher Education Students’ Critical Thinking Skills on Sustainability. International Journal of Engineering Education, 39(3):592-603.

Os paso el artículo, que está publicado en abierto. Espero que os sea de interés.

Descargar (PDF, 1.61MB)

Estudio de soluciones para el proyecto de una pasarela basado en un proceso analítico jerárquico

Durante los días 5-8 de julio de 2022 se celebró en Terrasa (Spain) el 26th International Congress on Project Management and Engineering AEIPRO 2022. Fue una buena oportunidad para debatir y conocer propuestas sobre dirección e ingeniería de proyectos. Nuestro grupo de investigación, dentro del proyecto de investigación HYDELIFE, presentó varias comunicaciones.

A continuación os paso una relacionada con el estudio de soluciones para el proyecto de una pasarela basado en un proceso analítico jerárquico (AHP).

Referencia:

YEPES-BELLVER, V.J.; ALCALÁ, J.; YEPES, V. (2022). Study of solutions for the design of a footbridge based on a hierarchical analytical process. 26th International Congress on Project Management and Engineering, AEIPRO, 5-8 de julio, Terrassa (Spain), pp. 512-524.

Os dejo un vídeo de la presentación realizada y la comunicación completa. Espero que os sean de interés.

Descargar (PDF, 1.16MB)

Ciclo de vida de puentes de hormigón en regiones costeras basada en el proceso analítico en red (ANP)

Acaban de publicarnos un artículo en Sustainability, revista indexada en el segundo cuartil del JCR. Se trata de aplicar la técnica de toma de decisiones en red ANP para evaluar la sostenibilidad del ciclo de vida de los puentes de hormigón en las regiones costeras. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València.

Desde que se establecieron los Objetivos de Desarrollo Sostenible en 2015, la evaluación de la sostenibilidad de las infraestructuras ha estado en el punto de mira de la comunidad científica. Esto se debe a que el sector de la construcción es esencial para promover el bienestar social y el desarrollo económico de los países, pero también es uno de los principales factores de estrés ambiental. Sin embargo, la evaluación de la sostenibilidad de las infraestructuras a lo largo de su ciclo de vida sigue siendo un reto importante, pues los criterios que intervienen en el diseño sostenible suelen ser complejos y contradictorios. El Proceso Analítico en Red (ANP) es una poderosa herramienta de toma de decisiones para modelar tales problemas. En este caso, se evalúa la sostenibilidad del ciclo de vida de diferentes alternativas de puentes de hormigón en ambiente costero utilizando el ANP. Los resultados obtenidos se comparan con los obtenidos mediante el Proceso Analítico Jerárquico (AHP) convencional. Los resultados obtenidos mediante ANP son más fiables que los derivados del AHP en términos de consistencia de los expertos y del número de comparaciones realizadas.

Abstract:

Since establishing the Sustainable Development Goals in 2015, the assessment of the sustainability performance of existing and future infrastructures has been in the spotlight of the scientific community. This is because the construction sector is essential for promoting the social welfare and economic development of countries, but is also one of the main environmental stressors existing to date. However, assessing infrastructure sustainability throughout its life cycle remains a significant challenge, as the criteria involved in sustainable design are often complex and conflicting. The Analytic Network Process (ANP) is recognized as a powerful decision-making tool to model such problems. Here, the life cycle sustainability performance of different design alternatives for a concrete bridge near the shore is evaluated using ANP. The obtained results are compared with those obtained using the conventional Analytical Hierarchy Process (AHP). The results obtained using ANP are more reliable than those derived from the conventional AHP in terms of the expert’s consistency and the number of comparisons made.

Keywords:

Sustainability; Analytic Network Process; bridge design; life cycle assessment; TOPSIS; multi-criteria decision making

Reference:

NAVARRO, I.J.; MARTÍ, J.V.; YEPES, V. (2022). Analytic Network Process-based sustainability life cycle assessment of concrete bridges in coastal regions. Sustainability, 14(17):10688. DOI:10.3390/su141710688

Como el artículo está publicado en abierto, os lo podéis descargar aquí mismo:

Descargar (PDF, 2.07MB)

Valoración económica del paisaje en los puertos deportivos: Aplicación a un puerto deportivo de la costa sur del Mediterráneo español (Granada, España)

Acaban de publicarnos un artículo en la revista Land, revista indexada en el JCR. En este caso se ha analizado la influencia mutua del paisaje y la gestión de los puertos deportivos. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València.

La asignación de un valor monetario a un bien inmaterial como es un paisaje permite valorar su verdadera importancia. Ayuda a darse cuenta de la magnitud de los beneficios que se pueden obtener y representa la base para aplicar políticas de protección y mejora. Como caso de estudio, consideramos Marina del Este, situada en la costa mediterránea meridional española, caracterizada por la presencia de espacios naturales protegidos de gran valor y un litoral abrupto de gran belleza para los navegantes. Este estudio aplica el método de valoración analítica multicriterio (AMUVAN) para estimar la contribución económica del paisaje. Este método combina el proceso de jerarquía analítica y el análisis de flujo de caja con descuento monetario. Se tuvo en cuenta a un total de 16 participantes, todos ellos con conocimientos sobre el puerto deportivo, entre los que se encontraban expertos en gestión del puerto deportivo, organizaciones de gestión con competencias en su entorno, explotación comercial y profesores universitarios. Se ponderó la importancia del paisaje en relación con el resto de las actividades del puerto deportivo, los valores de uso frente a los de no uso, y los componentes del valor económico total (VET) del paisaje dentro de los puertos deportivos como activo natural. Los resultados muestran que el paisaje, en este caso, puede alcanzar un valor de unos 16,3 millones de euros. Representa más del 3000% del valor de la cuenta de resultados del puerto deportivo. El análisis detallado de los componentes del VET permite proponer estrategias para mejorar el valor económico del paisaje.

ABSTRACT

Assigning a monetary value to a landscape improves its importance. It helps to realize the magnitude of the benefits that can be obtained and represents the basis for applying protection and improvement policies. As a case study, we considered Marina del Este, located on the Spanish Southern Mediterranean coast, characterized by the presence of protected natural areas of great value and a rugged coastline beautiful to sailors. This study applies the analytic multicriteria valuation method (AMUVAN) to estimate the landscape’s economic contribution. This method combines the analytic hierarchy process and discounted cash-flow analysis. A total of 16 participants were considered, all with knowledge about the marina, which included areas of the marina management, management organizations with competencies in the marina environment, commercial operation, and university professors. They weighted the importance of landscape concerning the rest of the marina activities, use versus non-use values, and the components of the total economic value (TEV) of the landscape within marinas as a natural asset. Results expressed that the landscape may reach a value of around 16.3 million euros. It represents more than 3000% of the value of the marina’s profit and loss account. A detailed analysis of the components of the TEV makes it possible to propose strategies to improve the economic value of the landscape.

Keywords:

Landscape; marinas; AHP; AMUVAN; economic value; management

Reference:

MARTÍN, R., YEPES, V. (2022). Economic valuation of landscape in marinas: Application to a marina in Spanish Southern Mediterranean coast (Granada, Spain). Land, 11(9):1400. DOI:10.3390/land11091400

Descargar (PDF, 875KB)

Valoración de activos por métodos multicriterio

Ya hemos escrito en este blog varios artículos sobre las técnicas de decisión multicriterio como AHP, ANP y DEMATEL. Estos métodos, que están pensados para tomar decisiones teniendo en cuenta varios criterios, tanto cuantitativos como cualitativos, se aprovechan de la capacidad del ser humano a la hora de realizar comparaciones uno a uno para un criterio, integrando y generalizando múltiples valoraciones pareadas. Sin embargo, resulta de interés conocer que se pueden aplicar estas herramientas a valoración de activos.

En efecto, estos métodos son útiles para valorar múltiples activos, tanto tangibles (inmuebles, fincas agrarias, bienes de mercado, empresas) como intangibles (fondos de comercio, marcas, patentes, recursos ambientales, obras de arte, daño moral). Consideran tanto las variables cuantitativas como las cualitativas, aquellas que no tienen medición directa y cuya valoración depende de la experiencia del tasador.

Son métodos que vienen a incorporarse a los métodos tradicionales de valoración de activos para ofrecerle al tasador más herramientas a la hora de efectuar valoraciones de activos cada vez más diversos.

A continuación os dejo un vídeo explicativo del profesor Jerónimo Aznar. También os recomiendo un curso gratuito sobre estos temas que puedes localizar en el siguiente enlace: https://www.edx.org/es/course/valoracion-de-activos-por-metodos-multicriterio

Referencias:

AZNAR, J. (2020). Curso de valoración de activos por métodos multicriterio AHP, ANP y CRITIC. Editorial Universitat Politècnica de València. Ref. 264.

AZNAR, J.; GUIJARRO, F. (2012). Nuevos métodos de valoración: modelos multicriterio. Editorial Universitat Politècnica de València.

SAATY, T.L., VARGAS, L. G. (2013). Decision making with the analytic network process: economic, political, social and technological applications with benefits, opportunities, costs and risks (Vol. 195). Springer Science & Business Media

ZHU, Q., DOU, Y., SARKIS, J. (2010). A portfolio-based analysis for green supplier management using the analytical network process. Supply Chain Management: An International Journal, 15(4), 306-319. https://doi.org/10.1108/13598541011054670

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Comunicaciones presentadas al 26th International Congress on Project Management and Engineering AEIPRO 2022

Durante los días 5-8 de julio de 2022 tendrá lugar en Terrasa (Spain) el 26th International Congress on Project Management and Engineering AEIPRO 2022. Es una buena oportunidad para debatir y conocer propuestas sobre dirección e ingeniería de proyectos. Nuestro grupo de investigación, dentro del proyecto de investigación HYDELIFE, presenta varias comunicaciones. A continuación os paso los resúmenes.

NAVARRO, I.J.; MARTÍ, J.V.; YEPES, V. (2022). ANP-based sustainability-oriented indicator for bridges in aggressive environments. 26th International Congress on Project Management and Engineering, AEIPRO, 5-8 de julio, Terrassa (Spain).

La presente comunicación presenta un indicador de sostenibilidad para la evaluación de las infraestructuras de puentes basado en el uso del Proceso Analítico en Red (ANP). Se presenta un análisis de sensibilidad sobre los resultados, discutiendo la aplicación del AHP convencional y de los procedimientos ANP más generales. Formulando el problema de decisión de forma cuantitativa, el método ANP ha arrojado resultados con una consistencia de más del doble que la obtenida mediante la técnica AHP frente al mismo problema de decisión, resultando ser más fiable al simplificar las comparaciones pareadas del experto.

NAVARRO, I.J.; VILLALBA, I.; YEPES, V. (2022). Development of social criteria for the social life cycle assessment of railway infrastructures. 26th International Congress on Project Management and Engineering, AEIPRO, 5-8 de julio, Terrassa (Spain).

El diseño sostenible de las infraestructuras requiere la consideración de los impactos económicos, ambientales y sociales. Desde la firma del Acuerdo de París, se han hecho grandes esfuerzos para desarrollar las metodologías orientadas a evaluar los impactos económicos y ambientales a lo largo del ciclo de vida de las infraestructuras. Sin embargo, la evaluación de la dimensión social en el diseño de las infraestructuras todavía requiere un desarrollo significativo. La presente comunicación propone un conjunto de indicadores sociales orientados a la evaluación del ciclo de vida de las infraestructuras ferroviarias. En particular, se presenta la evaluación de los impactos sociales de una vía férrea convencional con balasto. A continuación, se recomienda un indicador basado en la aplicación de procedimientos de toma de decisión multicriterio que ayudará en la elección del diseño de vía más ventajoso en términos sociales.

YEPES-BELLVER, V.J.; ALCALÁ, J.; YEPES, V. (2022). Study of solutions for the design of a footbridge based on a hierarchical analytical process. 26th International Congress on Project Management and Engineering, AEIPRO, 5-8 de julio, Terrassa (Spain).

El presente trabajo muestra la aplicación de la metodología AHP (Analytic Hierarchy Process) para realizar el estudio de soluciones necesario para el proyecto de una pasarela. Para ello se han planteado cuatro alternativas: viga de hormigón, hormigón ejecutado “in situ”, viga metálica y celosía metálica. Tras efectuar un estudio cualitativo de las ventajas e inconvenientes de las tipologías planteadas, se procede a establecer una jerarquía de criterios basados en la economía, la facilidad constructiva, la funcionalidad, la integración en el entorno, la estética y la durabilidad. A su vez, se han analizado once subcriterios dependientes de aquellos. Para evaluar las matrices de comparación pareada se ha procedido a una ronda de consultas a un grupo de cinco expertos que, por aproximaciones sucesivas, han acordado las valoraciones de comparación. Se ha comprobado, a su vez, la consistencia de todas las matrices de comparación utilizadas. Tras aplicar la metodología completa de toma de decisiones, la solución elegida, por su mayor valoración final, fue la pasarela en celosía.

Un nuevo modelo de toma de decisiones adaptativo basado en ANP y ELECTRE-IS aplicado a edificación

Acaban de publicarnos un artículo en Mathematics, revista indexada en el primer decil del JCR. Se trata de un nuevo modelo de toma de decisiones que utiliza variables cuantitativas y que se ha aplicado distintas estructuras de edificación. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València.

El proceso analítico en red (ANP) es un método discreto de toma de decisiones multicriterio (MCDM) concebido como una generalización del proceso analítico jerárquico (AHP) tradicional para abordar sus limitaciones. El ANP permite incorporar relaciones de interdependencia y retroalimentación entre los criterios y las alternativas que componen el sistema. Esto implica mucha más complejidad y tiempo de intervención, lo que reduce la capacidad del experto para emitir juicios precisos y coherentes. El presente trabajo aprovecha la utilidad de esta metodología formulando el modelo para variables exclusivamente cuantitativas, lo que simplifica el problema de decisión al dar lugar a un menor número de comparaciones pareadas. Se utilizan siete criterios relacionados con la sostenibilidad para determinar, entre cuatro alternativas de diseño para una estructura de edificio, cuál es la más sostenible a lo largo de su ciclo de vida. Los resultados revelan que el número de preguntas que requiere el AHP convencional se reduce en un 92%. Las ponderaciones obtenidas entre los grupos AHP y ANP muestran variaciones significativas de hasta el 71% en la desviación estándar relativa de algunos criterios. Esta sensibilidad a la subjetividad se ha llevado a cabo mediante la combinación de los métodos ANP-ELECTRE IS, permitiendo al experto reflejar la visión del problema de decisión con mayor flexibilidad y precisión. Tamién se ha analizado la sensibilidad de los resultados a los distintos métodos.

Abstract

The analytic network process (ANP) is a discrete multi-criteria decision-making (MCDM) method conceived as a generalization of the traditional analytic hierarchical process (AHP) to address its limitations. ANP allows the incorporation of interdependence and feedback relationships between the criteria and alternatives that make up the system. This implies much more complexity and intervention time, which reduces the expert’s ability to make accurate and consistent judgments. The present paper takes advantage of the usefulness of this methodology by formulating the model for exclusively quantitative variables, simplifying the decision problem by resulting in fewer paired comparisons. Seven sustainability-related criteria are used to determine, among four design alternatives for a building structure, which is the most sustainable over its life cycle. The results reveal that the number of questions required by the conventional AHP is reduced by 92%. The weights obtained between the AHP and ANP groups show significant variations of up to 71% in the relative standard deviation of some criteria. This sensitivity to subjectivity has been implemented by combining the ANP-ELECTRE IS methods, allowing the expert to reflect the view of the decision problem with greater flexibility and accuracy. The sensitivity of the results on different methods has been analyzed.

Keywords:

Multiple-criteria decision-making; sustainable design; analytic hierarchy process; analytic network process; ELECTRE IS; life cycle assessment; modern methods of construction

Reference:

SÁNCHEZ-GARRIDO, A.J.; NAVARRO, I.J.; GARCÍA, J.; YEPES, V. (2022). An Adaptive ANP & ELECTRE IS-based MCDM Model Using Quantitative Variables. Mathematics, 10(12):2009. DOI:10.3390/math10122009

Dejo a continuación el artículo, que se puede descargar y compartir, pues está publicado en abierto.

Descargar (PDF, 3.59MB)

Comparación de proyectos de vivienda de interés social considerando la sostenibilidad

Acaban de publicarnos un artículo en el International Journal of Environmental Research and Public Health, revista indexada en el JCR. Se trata de comparar distintas alternativas de viviendas sociales en Brasil, considerando la sostenibilidad. El trabajo se enmarca dentro del proyecto de investigación HYDELIFE que dirijo como investigador principal en la Universitat Politècnica de València y de la colaboración con el profesor Moacir Kripka.

Considerando la importancia del desarrollo de nuevos proyectos de vivienda, el propósito de esta investigación es proporcionar un modelo orientado a la identificación de la alternativa más sostenible en proyectos de vivienda unifamiliar de interés social desde la perspectiva del ciclo de vida y del proceso jerárquico analítico (AHP). Se evaluó un proyecto de mampostería cerámica y otro de mampostería de hormigón. En la dimensión ambiental, los resultados mostraron que el proyecto de albañilería cerámica tenía impactos ambientales más significativos y mayores daños a la salud humana y a la disponibilidad de recursos y ecosistemas. En la dimensión social, se comprobó que existen discrepancias entre los salarios de la cadena de suministro de la construcción y que el proyecto de mampostería de hormigón tenía mejores características sociales que el de mampostería cerámica. La dimensión económica reveló que el proyecto de mampostería de hormigón era más atractivo. Relacionando los resultados de las dimensiones ambiental, social y económica, se encontró que el proyecto de mampostería de hormigón presentaba una combinación de características más sostenibles que el proyecto de mampostería de cerámica en la mayoría de los resultados. Entre las implicaciones del estudio realizado aquí está el avance de la sostenibilidad aplicada al sector de la construcción.

Abstract:

Considering the importance of the development of new housing projects, the purpose of this research is to provide a model oriented to the identification of the most sustainable alternative in single-family housing projects of social interest from the perspective of life cycle thinking (LCT) and the analytical hierarchical process (AHP). A ceramic masonry project and a concrete masonry project were evaluated. In the environmental dimension, the results showed that the ceramic masonry project had more significant environmental impacts and greater damage to human health and the availability of resources and ecosystems. In the social dimension, it was found that there are discrepancies between the salaries in the construction supply chain and that the concrete masonry project had better social characteristics than the ceramic masonry project. The economic dimension revealed that the concrete masonry project was more attractive. Relating the environmental, social, and economic dimensions’ results, through the combination of LCT and AHP, it was found that the concrete masonry project presented a combination of more sustainable characteristics than the ceramic masonry project in the majority of the results. Among the implications of the study carried out here is the advancement of sustainability applied to the construction sector.

Keywords:

Social interest housing; life cycle thinking; analytic hierarchy process; sustainability

Reference:

VITORIO, P.C., Jr.; YEPES, V.; KRIPKA, M. (2022). Comparison of Brazilian Social Interest Housing Projects considering Sustainability. International Journal of Environmental Research and Public Health, 19(10):6213. DOI:10.3390/ijerph19106213 .

Descargar (PDF, 1.42MB)