transporte – El blog de Víctor Yepes

Transporte del hormigón en tiempo frío

El transporte del hormigón en tiempo frío debe realizarse con mayor cuidado para evitar interrupciones y retrasos en su puesta en obra. El calor generado en el interior de la cuba, si se trata de una amasadora, por el rozamiento del hormigón con las paredes y las palas, evita que el agua de amasado se congele, siempre y cuando el tiempo de permanencia no sea muy prolongado y las temperaturas ambientales no sean extremadamente frías. De lo contrario, sería necesario adoptar medidas especiales de aislamiento de las cubas. El suministro debe estar sincronizado con la puesta en obra para evitar esperas, tanto del hormigón ya colocado y desprotegido como de los camiones pendientes de descarga. Se recomienda que el tiempo de transporte desde la planta hasta la obra sea lo más breve posible.

Se pueden evaluar las pérdidas de temperatura del hormigón durante el transporte, expresadas en °C por cada hora, considerando el tiempo transcurrido entre el amasado y la colocación. Estas pérdidas se expresan como un porcentaje de la diferencia entre la temperatura prevista del hormigón en el momento de su colocación y la temperatura ambiente. El porcentaje de pérdida depende del tipo de transporte: 25 % en camiones hormigoneras, 20 % en camiones o recipientes abiertos, y 10 % en camiones o recipientes cubiertos.

Las bajas temperaturas ambientales en las que se va a transportar el hormigón afectan especialmente a los camiones hormigoneras. Estos vehículos, con su tambor metálico y su sistema de paletas, así como la canaleta, pueden estar extremadamente fríos, especialmente los primeros camiones de la mañana después de una noche de temperaturas gélidas y formación de hielo. En algunas regiones, se implementan medidas para contrarrestar estos efectos, como el uso de resistencias externas que generan calor en el tambor, el lavado con agua caliente o el estacionamiento de los camiones en espacios interiores.

En el caso del transporte por cinta, especialmente si es muy larga, se debe proteger el hormigón de la acción del viento para evitar su enfriamiento y desecación. Además, si se emplea una relación agua/cemento muy baja, también se debe proteger del secado.

En el caso del transporte por bombeo, si la tubería es muy larga, se recomienda aislarla para evitar el enfriamiento del hormigón.

Referencias:

AA. VV. (2002). Hormigones de ejecución especial (seis tipos). Colegio de Ingenieros de Caminos, Madrid, 114 pp.

ACI COMMITTEE 306. Cold wheather concreting (ACI 306R-16). American Concrete Institute.

AENOR (2022). UNE 83151-1 IN Hormigonado en condiciones climáticas especiales. Parte 1: Hormigonado en tiempo frío. Madrid, 27 pp.

CALAVERA, J. et al. (2004). Ejecución y control de estructuras de hormigón. Intemac, Madrid, 937 pp.

GALABRU, P. (1964). Tratado de procedimientos generales de construcción. Obras de fábrica y metálicas. Editorial Reverté, Barcelona, 610 pp.

MARTÍ, J.V.; YEPES, V.; GONZÁLEZ, F. (2014). Fabricación, transporte y colocación del hormigón. Apuntes de la Universitat Politècnica de València, 189 pp.

YEPES, V. (2020). Procedimientos de construcción de cimentaciones y estructuras de contención. Colección Manual de Referencia, 2ª edición. Editorial Universitat Politècnica de València, 480 pp. Ref. 328. ISBN: 978-84-9048-903-1.

YEPES, V. (2023). Maquinaria y procedimientos de construcción. Problemas resueltos. Colección Académica. Editorial Universitat Politècnica de València, 562 pp. Ref. 376. ISBN 978-84-1396-174-3

Cursos:

Curso de fabricación y puesta en obra del hormigón.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Maquinaria y procedimientos de construcción: Problemas resueltos

Os presento el libro que he publicado sobre maquinaria y procedimientos de construcción. Se trata de una completa colección de 300 problemas resueltos, abarcando aspectos relacionados con la maquinaria, medios auxiliares y procedimientos de construcción. Su contenido se enfoca en la mecanización de las obras, costos, disponibilidad, fiabilidad y mantenimiento de equipos, estudio del trabajo, producción de maquinaria, sondeos y perforaciones, técnicas de mejora del terreno, control y abatimiento del nivel freático, movimiento de tierras, equipos de dragado, explosivos y voladuras, excavación de túneles, instalaciones de tratamiento de áridos, compactación de suelos, ejecución de firmes, maquinaria auxiliar como bombas, compresores o ventiladores, cables y equipos de elevación, cimentaciones y vaciados, encofrados y cimbras, fabricación y puesta en obra del hormigón, organización y planificación de obras.

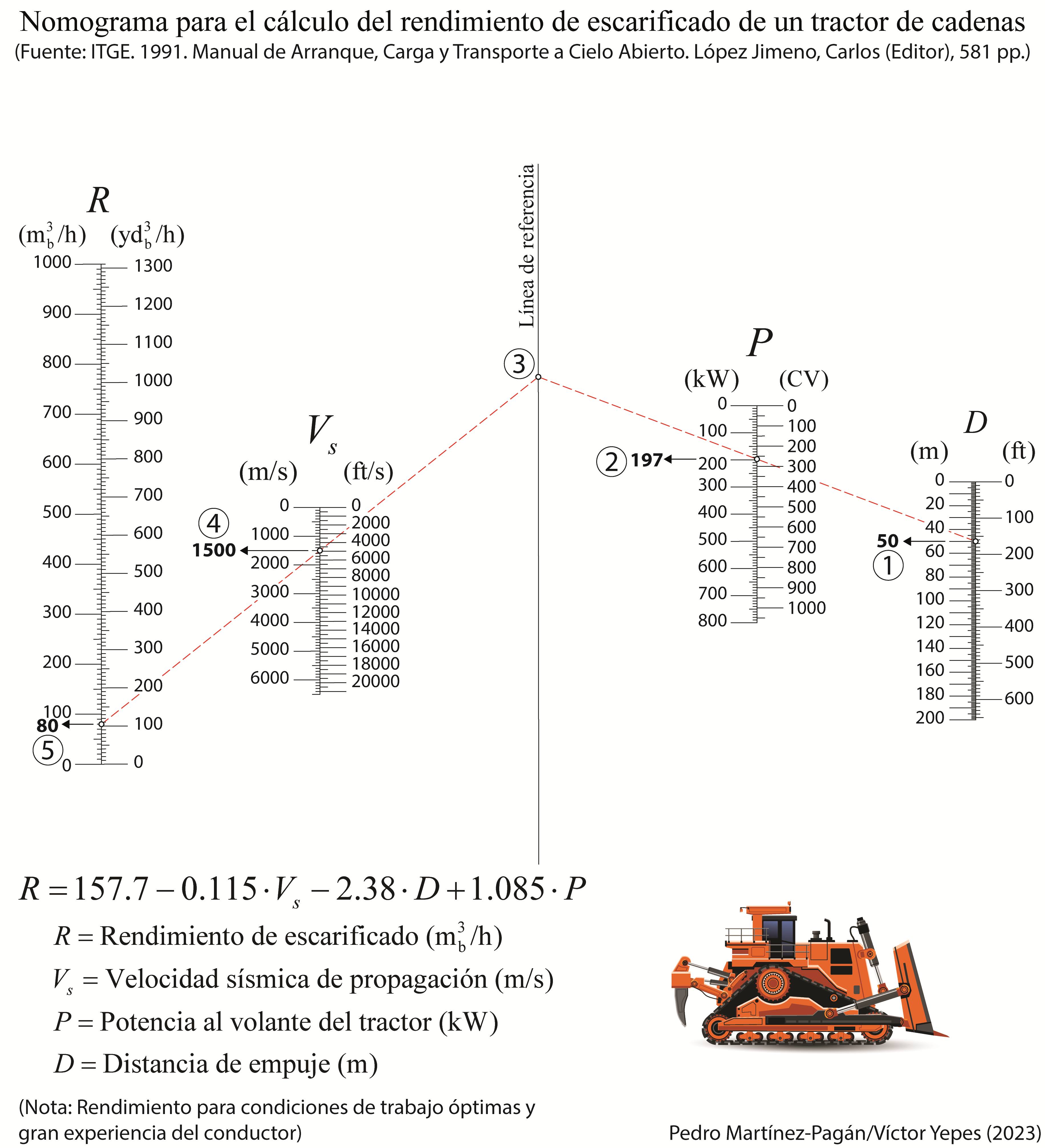
Es un libro, por tanto, muy enfocado a los ámbitos de la ingeniería de la construcción, tanto en el ámbito de la edificación, de la minería o de la ingeniería civil. Además, se incluyen 27 nomogramas originales y 19 apéndices para apoyar tanto a estudiantes de ingeniería o arquitectura, como a profesionales que enfrentan desafíos similares en su práctica diaria en obra o proyecto. La colección se complementa con un listado de referencias bibliográficas que respaldan los aspectos teóricos y prácticos abordados en los problemas. Estos problemas son similares a los tratados durante las clases de resolución de casos prácticos en la asignatura de Procedimientos de Construcción del Grado en Ingeniería Civil de la Universitat Politècnica de València (España). Por tanto, el libro resulta adecuado tanto para estudiantes de grado como para cursos de máster relacionados con la ingeniería civil y la edificación.

El libro tiene 562 páginas. Este libro lo podéis conseguir en la propia Universitat Politècnica de València o bien directamente por internet en esta dirección: https://www.lalibreria.upv.es/portalEd/UpvGEStore/products/p_376-7-1

Sobre el autor: Víctor Yepes Piqueras. Doctor Ingeniero de Caminos, Canales y Puertos. Catedrático de Universidad del Departamento de Ingeniería de la Construcción y Proyectos de Ingeniería Civil de la Universitat Politècnica de València. Número 1 de su promoción, ha desarrollado su vida profesional en empresas constructoras, en el sector público y en el ámbito universitario. Ha sido director académico del Máster Universitario en Ingeniería del Hormigón (acreditado con el sello EUR-ACE®), investigador del Instituto de Ciencia y Tecnología del Hormigón (ICITECH) y profesor visitante en la Pontificia Universidad Católica de Chile. Imparte docencia en asignaturas de grado y posgrado relacionadas con procedimientos de construcción y gestión de obras, calidad e innovación, modelos predictivos y optimización en la ingeniería. Sus líneas de investigación actuales se centran en la optimización multiobjetivo, la sostenibilidad y el análisis de ciclo de vida de puentes y estructuras de hormigón.

Referencia:

A continuación os paso las primeras páginas del libro, con el índice, para hacerse una idea del contenido desarrollado.

Descargar (PDF, 17.88MB)

Nomograma para el cálculo de la producción del ripado y transporte con un buldócer

Figura 1. Buldócer Cat D9T. https://commons.wikimedia.org/wiki/File:CatD9T.jpg

Uno de los ejemplos usuales es la producción de un buldócer (bulldozer, en inglés), que primero debe escarificar un terreno y luego debe empujarlo hasta una distancia de transporte determinada. En una entrada anterior dimos la resolución de la producción combinada de un buldócer.

Ahora os presentamos un nomograma elaborado junto con el profesor Pedro Martínez-Pagán sobre la producción del ripado y transporte con dicha máquina. Se han seguido las recomendaciones empíricas recogidas en el “Manual de arranque, carga y transporte en minería de cielo abierto” (Gómez de las Heras et al., 1995).

A continuación os voy a dar resuelto un problema de este tipo. Se trata de uno de los muchos casos que explicamos en el Curso de gestión de costes y producción de la maquinaria empleada en la construcción. Os animo a que, si estáis interesados, os informéis de este curso en línea.

Descargar (PDF, 1.17MB)

Referencias:

GÓMEZ DE LAS HERAS, J.; MANGLANO, S.; TOLEDO, J.; LÓPEZ-JIMENO, C.; LÓPEZ-JIMENO, E. (1995). Manual de arranque, carga y transporte en minería a cielo abierto. Instituto Geológico y Minero de España, Madrid, 604 pp.

YEPES, V. (1995). Maquinaria de movimiento de tierras. Servicio de Publicaciones de la Universidad Politécnica de Valencia. SP.UPV-264. 144 pp.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 256 pág. Depósito Legal: V-4598-1997. ISBN: 84-7721-551-0.

YEPES, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442. ISBN: 978-84-1396-046-3

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Ejercicios resueltos de sistemas de transporte continuo: bombas y cintas transportadoras

Tengo el placer de presentar un nuevo libro que acaba de salir de imprenta. Se trata de una colaboración con los profesores Pedro Martínez Pagán y Marcos A. Martínez Segura, de la Universidad Politécnica de Cartagena.

Es un libro que está editado en abierto, por lo que es posible su descarga gratuita. Se trata de un libro sobre ejercicios resueltos de sistemas de transporte continuo, centrado en bombas y cintas transportadoras.

Lo podéis descargar directamente en esta dirección del Repositorio Digital de la Universidad Politécnica de Cartagena: https://repositorio.upct.es/handle/10317/12154

Los problemas tipo que aquí se abordan son similares a los tratados durante las clases de resolución de problemas y casos prácticos que se imparten en la asignatura de Ingeniería Minera del Grado en Recursos Minerales y Energía (GIRME) de la Universidad Politécnica de Cartagena (España). De esta forma, el libro es apropiado para todos aquellos estudiantes de grado o cursos de máster relacionados con la industria mineral, de los áridos o de la obra civil; donde se presenta la necesidad de resolver problemas sobre bombeo de pulpas, elevación de agua, transporte de materias primas, etc.

Al final del texto se facilitan algunos libros y enlaces que los autores sugieren para completar o adquirir conocimientos que serían recomendables para la resolución de algunos de los problemas que aquí se presentan, así como las plantillas y ábacos utilizados en la resolución de los problemas. Los autores quieren agradecer las útiles sugerencias y aportaciones recibidas durante la elaboración de este trabajo por todos aquellos especialistas en esta materia, especialmente a D. Juan Luis Bouso Aragonés, presidente de Eral Chile, S.A.

También aquí, como en otros libros anteriores, esperamos y deseamos que su consulta sea útil y que el lector sepa disculpar posibles erratas que hayan podido producirse.

Resumen:

Este libro lo componen unos 40 problemas tipo totalmente resueltos, abordando la resolución de sistemas hidráulicos de bombeo para el transporte de aguas y pulpas y transporte de material sólido a granel por medio de cintas transportadoras, unidades imprescindibles encargadas de favorecer y mantener el flujo continuo entre unidades de procesos en la industria minera y civil. Por ello, estos equipos se encuentran instalados de una manera muy extendida en la industria: plantas de tratamiento de recursos minerales, petroquímicas, canteras para la fabricación de áridos, cementeras, obras civiles, etc. En definitiva, estos ejercicios resueltos pretenden ayudar a dimensionar y seleccionar adecuadamente estas unidades, siguiendo criterios internacionalmente establecidos, por lo que lo convierten en un libro de consulta idóneo para aquellos profesionales o especialistas relacionados con los procesos de minerales, las plantas de áridos, la construcción, la obra civil, etc.

Palabras clave:

Cintas transportadoras; bombas; transporte de graneles sólidos; transporte hidráulico de pulpas; sustancias minerales; mineralurgia; procesos minerales; materias primas

Referencia:

MARTÍNEZ-PAGÁN, P.; YEPES, V.; MARTÍNEZ-SEGURA, M.A. (2023). Ejercicios resueltos de sistemas de transporte continuo: bombas y cintas transportadoras. Ediciones UPCT. Universidad Politécnica de Cartagena, 284 pp.

También tenéis la opción de descargarlo aquí mismo:

Descargar (PDF, 16.1MB)

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Cálculo del transporte hidráulico de pulpas

Figura 1. Bomba horizontal de pulpas (Bouso y Martínez-Pagán, 2023)

Una pulpa es una mezcla líquida que contiene partículas sólidas en suspensión. Las características de la pulpa dependen de la naturaleza, tamaño, forma, densidad y cantidad de las partículas sólidas, así como de la naturaleza, densidad y viscosidad del líquido. El flujo de las pulpas es diferente al de los líquidos homogéneos, donde su naturaleza (laminar, transitorio o turbulento) se determina a partir de las propiedades físicas del líquido y su conductividad. Para calcular un sistema de transporte hidráulico de pulpa, compuesto por una bomba y una tubería, es esencial conocer previamente parámetros como la densidad de sólido y líquido, viscosidad, concentración de sólidos, tipo de tubería y topografía del terreno.

La caracterización de una pulpa es más compleja que la de un líquido debido a la presencia de partículas sólidas y su influencia en la mezcla. Es importante tener en cuenta que una pulpa no es una disolución, sino una suspensión de sólidos en líquidos donde cada componente está claramente definido. Debemos considerar el fenómeno de sedimentación de los sólidos en el líquido, especialmente cuando las turbulencias son bajas o no existen. Este fenómeno puede causar acumulaciones de sólidos y dificultar las operaciones de transporte o almacenamiento. En términos generales, las pulpas se pueden clasificar en dos grupos: pulpas sin sedimentación y pulpas con sedimentación.

Figura 2. Bomba de pulpas. https://www.mogroup.com/es/informacion/e-books/manual-de-bombas–para-pulpa/

Las pulpas sin sedimentación, también conocidas como pulpas homogéneas, están compuestas por partículas finas (menores de 50 mm) y forma una mezcla homogénea y estable. No causan desgaste significativo, pero requieren una atención especial en la selección y funcionamiento de las bombas debido a su aumento de viscosidad. Cuando el contenido de partículas es alto, su reología se asemeja a la de líquidos No-Newtonianos. Ejemplos de este tipo de pulpa incluyen lodos espesados de la extracción de áridos, lechadas de cemento y lodos de perforación.

Las pulpas con sedimentación están formadas por partículas gruesas que tienden a crear una mezcla inestable y se comportan como líquidos Newtonianos. Generalmente, causan un elevado desgaste y requieren una selección cuidadosa de las tuberías, debido a su tendencia a sedimentar y causar obstrucciones. Este tipo de pulpa es común en el transporte de pulpas y se conoce como pulpa heterogénea, ya que los sólidos no se distribuyen uniformemente en conducciones horizontales a lo largo de su eje vertical a altas velocidades. Las fases sólida y líquida mantienen su propia identidad y el aumento de viscosidad es generalmente de poca importancia. Las pulpas heterogéneas suelen ser de menor concentración de sólidos y con partículas de mayor diámetro que las pulpas homogéneas. Ejemplos incluyen pulpas en plantas de tratamiento de áridos y minerales, equipos de dragado, etc.

En el transporte de pulpas minerales por tubería, la naturaleza de las partículas y las velocidades de flujo determinan los regímenes de flujo, que pueden ser tanto turbulentos como laminares. Sin embargo, en la mayoría de las aplicaciones, el régimen turbulento, que se produce cuando las partículas son gruesas y tienden a sedimentar, es el más común. Este tipo de fluido se conoce como fluido newtoniano. En cambio, las pulpas con partículas finas y uniformes suelen producir regímenes de flujo laminar.

Os dejo a continuación un artículo, elaborado por Juan Luis Bouso y Pedro Martínez-Pagán, donde se presenta un ejemplo de cálculo para una operación de bombeo de pulpas. Se exploran las diferentes alternativas de cálculo, que pueden variar debido a las preferencias personales de los técnicos o a la adaptabilidad de un procedimiento específico a las características de la operación de bombeo. Al final del trabajo, se incluye un anexo con gráficos y cálculos, que pueden ser muy útiles. Espero que os sea de interés.

Descargar (PDF, 36.36MB)

Referencias:

ANDREA, E. (2014). Tecnología metalúrgica. Universidad de Cantabria. https://ocw.unican.es/course/view.php?id=261

BOUSO, J.L.; MARTÍNEZ-PAGÁN, P. (2023). Bombeo de pulpas minerales. Diferentes procedimientos de cálculo. Rocas y Minerales, 605:56-73.

LÓPEZ JIMENO, C. (ed.) (1998). Manual de áridos. Prospección, explotación y aplicaciones. 3ª edición, E.T.S. de Ingenieros de Minas de Madrid, 607 pp.

LÓPEZ JIMENO, C.; LUACES, C. (eds.) (2020). Manual de Áridos para el Siglo XXI. Asociación Nacional de Empresarios Fabricantes de Áridos— ANEFA, Madrid, 1328 pp.

MARTÍ, J.V.; GONZÁLEZ, F.; YEPES, V. (2005). Temas de procedimientos de construcción. Extracción y tratamiento de áridos. Editorial de la Universidad Politécnica de Valencia. Ref. 2005.165. Valencia, 74 pp.

MARTÍNEZ-PAGÁN, P.; PERALES, A. (2020). Tecnología metalúrgica, 2ª edición. Universidad Politécnica de Cartagena. https://ocw.bib.upct.es/course/view.php?id=178

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Costes de los neumáticos de la maquinaria de construcción

Figura 1. Neumáticos de dúmperes rígidos. Imagen: V. Yepes

Los costes de los neumáticos pueden representar en las grandes máquinas (tractores pesados, mototraíllas…) un tercio de su coste total. En algunos casos, los neumáticos se venden aparte, ajustándose al tipo de trabajo realizado por el equipo.

En condiciones ideales, la vida de servicio de unos neumáticos radiales es de unas 6.000 horas. Sin embargo, lo habitual son desgastes fuertes, por lo que se reponen, por término medio, entre las 2.500 a 4.000 horas de trabajo (de 30.000 a 50.000 km). En el caso de mototraíllas o palas cargadoras en condiciones de gran dureza, la vida se reduce a unas 1.000 horas.

Para comparar la vida de los neumáticos se puede utilizar el concepto de T.V.H. que representa el producto de las toneladas medias transportadas por la velocidad media y por las horas recorridas. A mayor T.V.H., mejor comportamiento del neumático.

Las condiciones que más inciden en la duración de los neumáticos son los impactos, que producen dobleces y descascarillados, la abrasión y otros factores que dependen de las condiciones naturales y del terreno, del tipo y hábitos del operador y del mantenimiento realizado. En la Tabla 1 se recoge la duración estimada, en función de las condiciones de trabajo, para los neumáticos de distintas máquinas.

Tabla 1. Duración típica de los neumáticos, en horas (Nunnally, 2001)

Tipo de equipo	Condiciones de trabajo
Tipo de equipo	Favorables	Medias	Desfavorables
Buldócer o cargadora	3.200	2.100	1.300
Motoniveladora	5.000	3.200	1.900
Mototraílla convencional	4.600	3.300	2.500
Mototraílla de doble tracción	4.000	3.000	2.300
Mototraílla push-pull y autocargable	3.600	2.700	2.100
Dúmper extravial y motovagón	3.500	2.100	1.100

En la Tabla 2 se indican los factores que habría que aplicar para calcular la longevidad de los neumáticos en el caso de equipos de acarreo para movimiento de tierras.

Tabla 2. Factores que reducen la longevidad de los neumáticos en vehículos de transporte de movimiento de tierras

Eje motriz	Tracción continua a 4 ruedas	0,9
	Tracción intermitente a 4 ruedas	0,8
	Eje de apoyo	1,0
Presión de inflado	Presión correcta	1,0
Presión de inflado	Presión de inflado un 10% inferior	0,9
Carga	Ninguna sobrecarga	1,0
	10% sobrecarga	0,9
	20% sobrecarga	0,8
Condiciones de la rodadura o ruta de transporte	Tierra blando con un poco de piedras	1,0
	Camino de grava bien mantenido	1,0
	Camino de grava mal mantenido	0,9
	Rocas dinamitadas	0,7
Mantenimiento del sitio de carga y descarga	Excelente	1,0
Mantenimiento del sitio de carga y descarga	Deficiente	0,9
Curvas	Ninguna o muy suaves	1,0
Curvas	Cerradas	0,9
Pendientes (solo para las ruedas motrices)	No pasan del 6%	1,0
Pendientes (solo para las ruedas motrices)	Superior al 6%	0,9
Velocidad media	16 km/h	1,0
Velocidad media	32 km/h	0,9
Experiencia del operador	Más de 6 meses	1,0
Experiencia del operador	Menos de 6 meses	0,9

Por ejemplo, la longevidad de los neumáticos radiales de un dúmper pasa de 6.000 horas a 3.540 horas al aplicar el producto de todos los coeficientes (0,59) en el caso siguiente: presión de inflado recomendada, sobrecarga del 10%, camino de transporte de grava deficientemente mantenido, mantenimiento-conducción, carga, descarga defectuoso, curvas suaves, pendientes que no sobrepasan el 6%, velocidad media aproximada de 32 km/h y operador con experiencia.

En la Tabla 3 se adjunta una tabla parecida donde se recogen los factores de reducción de la vida de los neumáticos (Solminihan y Thenoux, 2008).

Tabla 3. Factores de reducción de la vida de los neumáticos (Solminihan y Thenoux, 2008)

Condiciones de uso	Factor a aplicar
Condiciones de uso	1,0	0,9	0,8	0,7	0,6
Presión del neumático (kg/cm²), en comparación con la especificada	100%	90%	80%	75%	70%
Carga del neumático, en comparación con la especificada	100%	129%	139%	150%	—
Velocidad media (km/h)	16	24	32	40	48
Posición de la rueda	Traseras de arrastre	Frontales	De tracción en vagonetas de acarreo de materiales		Motora
Clase de superficie del recorrido	Tierra blanda, suave o suelta	Camino de grava, grava angulosa			Roca angulosa

Como la vida de los neumáticos es inferior a la de la máquina, los costes de propiedad y de operación de ambos se estudian por separado. Así, la amortización de este tipo de maquinaria se hará deduciendo el coste de las cámaras y neumáticos del de adquisición de aquella. Su coste horario se calcula como la relación entre el coste de las cámaras y de los neumáticos y las horas de vida útil, considerando un 10% sobre el costo por reparaciones: recauchutados, pinchazos, etc.

Referencias:

NUNNALLY, S.W. (2001). Construction Methods and Management. 5th edition, Prentice Hall, New Yersey, 549 pp.

SOLMINIHAC, H.; THENOUX, G. (2008). Procesos y técnicas de construcción. Quinta edición, Ediciones de la Universidad Católica de Chile, Santiago, Chile, 545 pp.

YEPES, V. (1997). Equipos de movimiento de tierras y compactación. Problemas resueltos. Colección Libro Docente n.º 97.439. Ed. Universitat Politècnica de València. 253 pág.

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Producción combinada de un equipo con varias tareas: el caso de un buldócer

Buldócer Caterpillar D9T. https://commons.wikimedia.org/wiki/File:CatD9T.jpg

Es habitual encontrarnos con equipos que, aunque trabajen de forma aislada, deban realizar varios tipos de trabajos consecutivos para acabar de terminar una tarea. Además, en cada uno de estos trabajos, su producción es diferente. El problema es calcular la producción combinada conjunta. Uno de los ejemplos usuales es la producción de un buldócer (bulldozer, en inglés), que primero debe escarificar un terreno y luego debe empujarlo hasta una distancia de transporte determinada.

Descargar (PDF, 258KB)

Referencias:

YEPES, V. (1995). Maquinaria de movimiento de tierras. Servicio de Publicaciones de la Universidad Politécnica de Valencia. SP.UPV-264. 144 pp.

Curso:

Curso de gestión de costes y producción de la maquinaria empleada en la construcción

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Problema resuelto sobre distancia crítica de transporte

En un artículo anterior definimos la distancia crítica de transporte en un movimiento de tierras como aquella distancia en la que el equipo de cargadoras y camiones está equilibrado. Es decir, ni sobran ni faltan camiones o cargadoras. O dicho de otra forma, es la distancia de transporte en la que no existen esperas en las máquinas. Esta es una distancia teórica, puesto que para calcularla debemos conocer todos los datos de antemano, y estos no son deterministas. Por otra parte, en obra ocurre lo contrario: tenemos una distancia de transporte como dato, pero en este caso se trataría de saber cuántos camiones y cargadoras serían necesarios para que no existiesen demoras. Afortunadamente en obra se puede corregir rápidamente cualquier desfase. En dicho artículo proporcionamos, incluso, una calculadora en línea para que se pudiesen visualizar los cambios.

Aquí lo que presento es un problema resuelto que, espero, os sea de interés. Este problema lo puse en su momento en un examen de Procedimientos de Construcción, en la ETS de Ingeniería de Caminos, Canales y Puertos de Valencia.

Descargar (PDF, 203KB)

Referencias:

YEPES, V. (1995). Maquinaria de movimiento de tierras. Servicio de Publicaciones de la Universidad Politécnica de Valencia. SP.UPV-264. 144 pp.

Desarrollo de criterios sociales para la evaluación del ciclo de vida social de las infraestructuras ferroviarias

El diseño sostenible de las infraestructuras requiere la consideración de los impactos económicos, ambientales y sociales. Desde la firma del Acuerdo de París, se han hecho grandes esfuerzos para desarrollar las metodologías orientadas a evaluar los impactos económicos y ambientales a lo largo del ciclo de vida de las infraestructuras. Sin embargo, la evaluación de la dimensión social en el diseño de las infraestructuras todavía requiere un desarrollo significativo. La presente comunicación propone un conjunto de indicadores sociales orientados a la evaluación del ciclo de vida de las infraestructuras ferroviarias. En particular, se presenta la evaluación de los impactos sociales de una vía férrea convencional con balasto. A continuación, se sugiere un indicador basado en la aplicación de procedimientos de toma de decisión multicriterio que ayudará en la elección del diseño de vía más ventajoso en términos sociales.

ABSTRACT

The sustainable design of infrastructures requires the consideration of the economic, environmental, and social impacts. Since the establishment of the Paris Agreement, significant efforts have been made on the methodologies to assess infrastructures’ economic and environmental life cycle impacts. However, evaluating the social dimension in the design of infrastructures still requires significant development. The present communication proposes a set of social indicators oriented towards the life cycle assessment of railway infrastructures. In particular, the evaluation of the social impacts of a conventional ballasted rail track is presented. A multi-criteria decision-making procedure-based indicator is proposed to help decide the most advantageous track design in social terms.

Keywords:

Multi-criteria Decision-making; Sustainability; Life cycle assessment; Railway; Social impacts.

Reference:

NAVARRO, I.J.; VILLALBA, I.; YEPES, V. (2022). Development of social criteria for the social life cycle assessment of railway infrastructures. 26th International Congress on Project Management and Engineering, AEIPRO, 5-8 de julio, Terrassa (Spain).

Os dejo la presentación que hicimos en el congreso y la comunicación completa.

Descargar (PDF, 329KB)

Conferencia magistral sobre optimización sostenible del mantenimiento de carreteras

Os dejo a continuación la grabación de la Conferencia Magistral que tuve la ocasión de presentar en el Congreso Nacional de Ingeniería Civil 2021. Dicho evento tuvo lugar en la modalidad virtual del 28 de junio al 02 de julio del 2021. El Congreso Nacional de Ingeniería Civil es el evento que reúne a profesionales, docentes, investigadores y empresarios del sector de la construcción en una jornada de capacitación acerca de las últimas innovaciones producto de las actividades de investigación en el sector de la construcción. Agradezco, una vez más, al Consejo Departamental de ICA del Colegio de Ingenieros del Perú – Capítulo de Ingeniería Civil, la deferencia que tuvo conmigo al invitarme a participar en su Congreso.