septiembre 2017 – El blog de Víctor Yepes

Introducción a la técnica de construcción de puentes por voladizos sucesivos

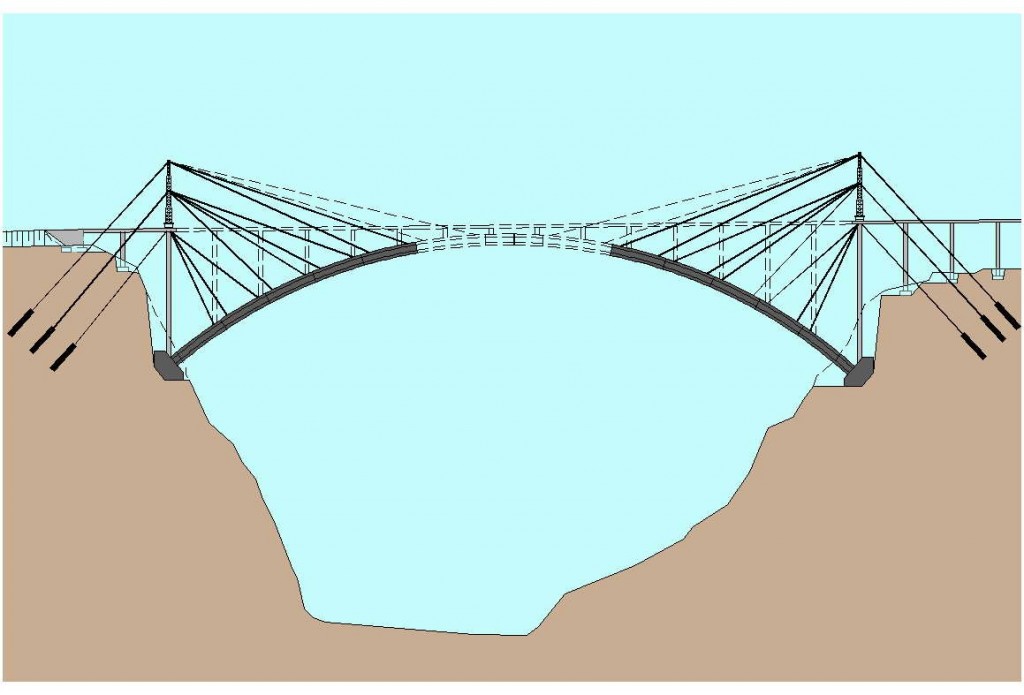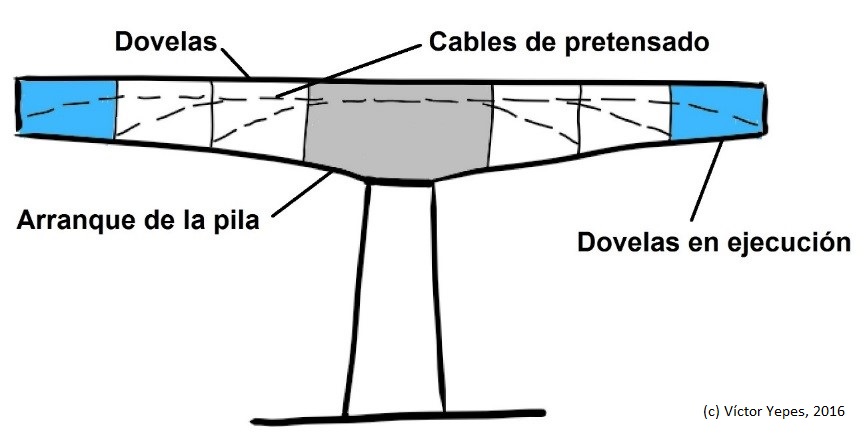
Esquema del principio de la construcción por voladizos

La construcción por tramos o dovelas, prefabricadas o ejecutadas “in situ”, que avanzan en voladizo sobre las ya erigidas. El tablero avanza por tramos sucesivos soportando la parte construida el peso propio del tramo siguiente. La construcción en voladizo permite liberarse de cimbras y andamios, adaptándose especialmente a puentes con pilas muy altas, con valles extensos y profundos, en ríos con crecidas violentas y repentinas o bien cuando hay que dejar libre un gálibo para la circulación o la navegación.

Este procedimiento se puede usar en puentes rectos, arco y atirantados, de hormigón o metálicos. Las dovelas prefabricadas se izan con medios de elevación potentes y se unen a las anteriores. Si se ejecutan hormigonando “in situ”, existe un carro de avance que se apoya en las dovelas anteriores, asegurando la estabilidad de cada etapa con el pretensado de cables cuando la nueva dovela adquiere la resistencia suficiente.

La técnica del voladizo se utilizó en el siglo XIX en el lanzamiento de obras metálicas, en la construcción de grandes arcos y “cantilever”. Con la llegada del hormigón armado, este procedimiento empezó a interesal a los constructores. El primer puente construido por voladizos sucesivos fue el puente sobre el río Peixe en Herval (Brasil), data de 1930, siendo su autor Emilio Henrique Baumgart; se trata de un puente de hormigón armado de dintel continuo de tres vanos, con 68 m de luz en el central. En este puente las armaduras del tablero se extendían mediante manguitos roscados a medida que avanzaba el hormigonado. Sin embargo, con hormigón armado se necesitaban muchas armaduras para asegurar la resistencia de las ménsulas y aparecía una fuerte fisuración en el extradós del tablero, lo que provocó que el sistema no tuviese mucho éxito.

Puente de Balduinstein, sobre el Lahn (Alemania). Foto: Claudia Lenau. Fuente: http://structurae.net/photos/132164-balduinstein-bridge

Sin embargo, con el hormigón pretensado el sistema empezó a desarrollarse plenamente. Así, Freyssinet empezó a utilizar el pretensado para el montaje en voladizo en las primeras dovelas del puente de Luzancy en 1945 y de los cinco puentes sobre el Marne, anclados en los estribos por pretensado. Pero es Finsterwalder quien inicia definitivamente la técnica del voladizo en 1950 en el puente de Balduinstein, sobre el Lahn, con 62,10 m de luz libre, cuando aplica esta tecnología con un pretensado a base de barras que se unían entre sí mediante un sistema roscado. En España, fue empleado en sus orígenes en el puente de Almodóvar (1962) y el de Castejón (1968).

En la construcción con dovelas prefabricadas se pueden distinguir tres etapas. La primera generación, en los años sesenta, las dovelas llevaban juntas de mortero de cemento, llave única a cortante y cables anclados en la propia junta. La segunda se caracteriza por la prefabricación conjugada, el empleo de resinas epoxi en las juntas, las llaves múltiples para el cortante y el anclaje de los cables en el interior de la dovela en unos bloque dispuestos al efecto. La tercera generación, iniciada en Francia, utiliza el pretensado exterior y las almas de celosía (puente de Bubiyán en Kuwait, 1983).

La construcción por voladizos sucesivos puede realizarse con una única dirección de avance, la denominada construcción evolutiva; o bien con crecimiento simétrico del tablero a ambos lados de las pilas, voladizos compensados. En el primer caso, se suprime uno de los inconvenientes de la progresión simétrica del tablero, con la consecuente multiplicación de equipos (uno por cada frente de avance) o su traslado.

El campo habitual de aplicación de los puentes construidos por voladizos sucesivos abarca luces entre 50 y 250 m. Sin embargo, y de forma excepcional, pueden encontrarse puentes con luces de 400 m construidos por voladizos sucesivos con dovelas atirantadas de forma provisional. Por debajo de 50 m de luz tampoco es muy corriente. A partir de los 200-300 m, se entra en competencia con los puentes atirantados. El rango de luces usual para dovelas “in situ” es de 125 a 175 m, mientras que para las prefabricadas es algo menor, de 60 a 130 m.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Apoyos deslizantes para el lanzamiento de puentes

apoyo deslizante — Apoyo deslizante, con almohadillas de neopreno-teflón. Fuente: Óscar Ramos, 2010

El procedimiento de tableros empujados consiste en fabricar o montar el tablero detrás del estribo y después empujarlo deslizándolo sobre las pilas hasta alcanzar su posición definitiva al llegar al otro estribo. Para que ello sea posible, el tablero del puente debe deslizarse en todos los puntos donde se apoya, ya sean pilas, estribos o en el parque de fabricación. Estos apoyos, que en principio eran rodillos, hoy son de neopreno-teflón, que ofrecen poca fricción y una excelente distribución de las cargas verticales. Los apoyos pueden ser provisionales o definitivos. Los primeros se usan sobre apoyos auxiliares o en el parque de fabricación. Sobre las pilas pueden ser también provisionales, en cuyo caso se sustituyen posteriormente, o bien definitivos, con un segundo nivel deslizante que se utiliza durante el lanzamiento del tablero.

En los puentes de hormigón, el apoyo provisional se monta sobre un bloque de hormigón de unos 15-35 cm de espesor, fuertemente armado y nivelado. Sobre el hormigón se dispone una chapa de acero inoxidable pulida y plana, sobre la que se disponen las almohadillas de neopreno-teflón, de 10-13 mm de espesor. En los puentes de hormigón, el teflón se apoya sobre el acero inoxidable y el neopreno contacta con el tablero. Además, el apoyo dispone de una guía lateral, también con almohadillas de neopreno-teflón, que encarrila al tablero en su movimiento longitudinal. En el caso de puentes de acero o mixtos, se coloca la pastilla fija en el apoyo, con el teflón hacia arriba, siendo el puente el que desliza sobre la pastilla. En los puentes metálicos, muchos más flexibles, los apoyos pueden ser rotulados, de forma que se van adaptando a la deformada y a las contraflechas del tablero durante cada fase de lanzamiento.

En el caso de puentes de hormigón, el movimiento del tablero arrastra la almohadilla, que cae por delante y se vuelve a introducir por detrás. Esta operación se realiza manualmente, por lo que se debe prestar especial atención a los posibles errores durante las 2-3 horas que dura la operación del lanzamiento del tramo correspondiente. En los puentes metálicos, al permanecer el teflón fijo, no se precisan operarios recolocando continuamente las pastillas.

El coeficiente de rozamiento entre la almohadilla y el acero inoxidable, en el momento del arranque, puede llegar al 5% en tiempo frío, pero una vez en movimiento, baja al 3-3,5%. Para reducir la carga horizontal sobre el apoyo, se reducen al máximo las almohadillas, pues el rozamiento se reduce con la presión. Para soportar la carga vertical, se zuncha intensamente el neopreno para soportar unos 20 MPa. Además, conviene lubricar las almohadillas con silicona y mantenerlas limpias, con lo que se puede bajar el rozamiento al 1-2%.

Los apoyos provisionales se sustituyen por los definitivos subiendo el tablero con gatos. Esto mismo se debe hacer incluso cuando los apoyos deslizantes son definitivos, puesto que se debe bloquear el nivel de deslizamiento usado durante el lanzamiento, quitar las almohadillas y soldar la parte superior del apoyo a chapas metálicas dejadas en el tablero.

En puentes de hormigón se pueden lanzar vanos de 20 a 70 m, pudiendo ser de hasta más de 100 m en los metálicos. Con una buena velocidad de empuje, de unos 10 m/h, el lanzamiento se puede prolongar toda una jornada.

Se agradecen los comentarios realizados por Juan José Martí Gastaldo a este artículo, especialmente en lo referente a los puentes metálicos.

Os dejo a continuación un vídeo donde se observa el lanzamiento del tablero.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Pinceladas acerca de la ingeniería en la antigua China

Quin Shi Huang, fundador de la Dínastia Quin.

En entradas anteriores ya hemos hecho mención a la ingeniería primitiva, la desarrollada en Mesopotamia o en la Grecia Clásica. Mención especial merecen los desarrollos alcanzados en la Antigua China, que en el siglo I ya tenía 57 millones de habitantes, superando a Roma, aunque ambos imperios apenas llegaran a conocerse entre ellos. Por tanto, hoy vamos a dar dos pinceladas a las realizaciones de la milenaria China, sabiendo que dejamos muchísima información por el camino. Los cuatro grandes inventos chinos fueron el papel, la brújula, la pólvora y la imprenta.

Una de las más grandes realizaciones de todos los tiempos fue la Gran Muralla China, con más de 4 km de muro en total. Esta muralla tiene unos 10 m de altura, 8 m de espesor en la base y 5 m en la parte superior, por donde discurre un camino pavimentado. Su construcción requirió un elevado número de personas. Los bloques de piedra se traían con rodillos a las zonas previamente excavadas para su colocación. Su construcción se complicaba en zonas con fuertes vientos o en otras de clima desértico. Los materiales empleados fueron los disponibles en cada sitio: piedra caliza, granito o ladrillo cocido. Especialmente eficaz a los impactos de armas de asedio fueron las tapias de arcilla y arena cubiertas con varias paredes de ladrillo. Para hacerse una idea, en el reinado de Qin Shi Huang, que empezó a gobernar en el 221 a.C., se construyeron caminos y vías. Nada menos que 6.800 km durante sus 20 años de imperio, lo cual es muy llamativo si tenemos en cuenta que los romanos, 300 años después, tuvieron un total de 5.984 km, casi mil menos.

Vista parcial del sistema de irrigación de Dujiangyan.

También China tuvo canales desde hace miles de años. El sistema de irrigación de Dujiangyan comenzó en el siglo III a.C., basándose su construcción en un canal que tuvo que atravesar una montaña, lo cual no fue una tarea fácil teniendo en cuenta los procedimientos constructivos de la época. Para salvar dicho problema, se recurrió al calentamiento y enfriamiento repetido de la roca, lo cual fractura la roca y permitía su excavación. Para evitar la acumulación de limo en el sistema de irrigación, se construyó un dique en el centro del río, cimentados en unos enormes gaviones hechos de bambú. Además, fueron los primeros constructores de puentes, con características únicas. Algunos de sus puentes más antiguos fueron de suspensión, con cables hechos de fibra de bambú. Aunque sin basarse en teorías científicas, los antiguos constructores chinos empleaban un método que está relacionado con los “drenes de arena”. En sus suelos aluviales blandos hincaban pilotes de madera que extraían, a continuación, por rotación. Los agujeros eran rellenados con cal viva bien compactada. Estos pozos de cal absorbían el agua que los rodeaba, produciendo, de este modo, una consolidación acelerada del suelo, siendo estos los principios del empleo de las técnicas de mejora del terreno.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Concepto de puente viga y algo de historia

Puente en cajón postesado sobre el Turia (Quart de Poblet). Proyectado por Javier Manterola y construido por Dragados y Construcciones en 1991.

Una viga constituye una pieza lineal apoyada que resiste fundamentalmente a flexión. Estas estructuras presentan un canto e inercia crecientes con luz, puesto que la flexión es directamente proporcional al cuadrado de la luz. Los puentes viga, por tanto, se basan en secciones de máxima inercia y de mínimo peso (secciones en doble T, cajones, etc.).

Aunque morfológicamente el puente viga puede parecer el sistema más simple y directo de atravesar un río, su mecanismo resistente, la flexión, es más complejo y difícil de intuir que el esfuerzo axil, ya sea de tracción o compresión, predominante en otras tipologías estructurales, como los arcos (ver un post anterior).

Las primeras intuiciones sobre el mecanismo de la flexión en una viga surgen en el Renacimiento con Leonardo da Vinci, aunque fue Galileo el primero que intentó dar una explicación científica al comportamiento de una viga. Sin embargo, fue Coulomb (1736-1806) el primero que propuso las condiciones de equilibrio de las secciones de la viga y Navier (1785-1836) el que resolvió en 1824 completamente el problema basándose en la proporcionalidad de tensiones y deformaciones (ley de Hooke) y en la hipótesis de la conservación de las secciones planas. Continuadores de Navier fueron Saint-Venant y Bresse que hicieron importantes aportaciones a la resistencia de materiales y al cálculo de las estructuras hiperestáticas. Sin embargo, no fue hasta 1954 el año en que Livesley inició el método matricial del cálculo de estructuras empleado hoy masivamente con el empleo de los ordenadores personales.

La modelización para el cálculo de un puente viga puede seguir un análisis como estructura lineal. Sin embargo, el tablero del puente es una superficie y, por tanto, deber estudiarse adecuadamente el efecto del reparto de las cargas. En los puentes oblicuos se requiere incluso un estudio tridimensional de tensiones. Es habitual, en consecuencia, utilizar modelos de cálculo bidimensionales basados en la losa ortótropa (rigideces distintas en las dos direcciones). Es habitual el empleo del modelo del emparrillado, el de láminas plegadas, el de bandas o de elementos finitos.

En cuanto a las soluciones estructurales, estas han pasado, según crecía la luz a salvar por el puente, por la losa maciza, la losa aligerada, el tablero de vigas de alma llena, las vigas en celosía o trianguladas y las vigas cajón. Con las triangulaciones se llega a la máxima reducción de material, constituyendo los puentes viga que cubren las luces mayores. Sin embargo, en las vigas cajón se consigue la máxima eficacia resistente por su excelente comportamiento tanto a flexión como a torsión.

Las vigas pueden estar simplemente apoyadas en sus extremos, o bien ser vigas continuas, es decir, apoyadas en varios puntos. Los puentes viga biapoyados constituyen estructuras isostáticas, de cálculo sencillo, que han sido empleados para cubrir pequeñas y medianas luces. Los puentes en viga continua son estructuras hiperestáticas, que permiten reducir considerablemente la flexión de cálculo, debido al cambio de signo de estos esfuerzos en los apoyos y en el centro del vano.

Los puentes continuos presentan ciertas ventajas frente a los simplemente apoyados. Se requiere un menor número de apoyos y de juntas (superficie de rodadura sin interrupciones), los cantos son menores y, asimismo, la deflexión y la vibración son menores. Sin embargo, los asientos diferenciales pueden afectar a la estructura. Otro inconveniente, aunque menor, es la mayor complejidad en el análisis del puente continuo, sin embargo, es una dificultad relativa con los potentes medios de cálculo actuales. Además, en los puentes prefabricados, es habitual un sistema constructivo evolutivo que pasa del isostatismo al hiperestatismo al unir las piezas prefabricadas a una losa de hormigón y además se da una continuidad longitudinal. En estos casos deben contemplarse las redistribuciones de esfuerzos en el tiempo por la fluencia y retracción del hormigón, y si, además, la sección evoluciona, aparecen también redistribuciones internas de tensiones. Estas redistribuciones no son despreciables y deben considerarse en el cálculo, en el proyecto y en la construcción.

Una tercera opción lo constituyen las vigas Gerber o en cantilever, que introducen articulaciones en una viga continua con tal de hacerla isostática. En este último caso se suman las ventajas de las vigas continuas (cambio de signo en los momentos) y las vigas biapoyadas (no se ven afectadas por asientos del terreno).

Los puentes viga se han construido con materiales tan diversos como la madera, el acero, el hormigón armado y el hormigón pretensado. Los puentes de vigas en celosía y trianguladas en madera se desarrollaron en el siglo XIX sobre todo en Estados Unidos con la extensión del ferrocarril. Se llegó con vigas Town de madera a luces de 70 m en el puente de Blenheim en 1853. En 1840 Howe patentó la primera viga mixta de madera y hierro; sin embargo, pronto se impusieron las vigas puramente metálicas.

Hacia 1830 la producción industrial de hierro comienza a desarrollarse con el ferrocarril, y con ello se recurrió a este nuevo material en forma de vigas trianguladas o de vigas de alma llena. En esta última categoría destaca el puente Britannia, sobre el Menai (Gales), finalizado en 1850 por Stephenson, con dos tramos centrales de 140 m de luz.

La sección de caja original del Puente Britannia, circa 1852.

A finales del siglo XIX el acero sustituyó completamente al hierro y, por supuesto, a la fundición. Los puentes viga de acero se impusieron rápidamente por su ligereza. Para luces medias, y por encima de los 75 m, las soluciones metálicas entran en competencia con el hormigón pretensado. La luz de 300 metros del vano central de puente de Niteroi (Río de Janeiro, Brasil) se puede considerar límite en puentes metálicos en viga continua con sección en cajón, porque la solución más adecuada para estas luces es la atirantada. Otras tipologías, como los puentes atirantados o los colgantes, quedan fuera de la clasificación de los puentes viga.

Tampoco se entrará en la descripción de los puentes viga de hormigón armado, pues estos quedan relegados a las pequeñas obras de fábrica (menos de 15 m de luz), estando ampliamente superada su tecnología con el hormigón pretensado para luces mayores. Sin embargo, el puente viga de hormigón armado de mayor luz del mundo es la pasarela de Irvy sobre el Sena (París), con 134,5 m de luz, construida en 1930; su tipología corresponde con una viga triangulada. Para otros post dejamos los aspectos constructivos de estos puentes.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

El concepto de puente

Puente Ingeniero Carlos Fernández Casado, en embalse de Barrios de Luna (León). Imagen: © V. Yepes

Los puentes pueden considerarse como una de las construcciones cuyos orígenes se pierden en los albores del tiempo. Son las obras civiles por excelencia. Sin embargo, son mucho más que simples construcciones, en palabras de Juan José Arenas, “un puente ha sido, y es, sin género de dudas, un elemento indispensable para el desarrollo de la civilización y de la cultura”.

Los puentes a lo largo de la historia han identificado paisajes y se han erigido en articuladores del espacio. Javier Manterola recuerda que “el puente es un elemento del camino”, por tanto, no puede entenderse sin él, pero tampoco sin el obstáculo. Es el paradigma del esfuerzo de la razón en su pretensión de superar todo tipo de dificultad y contratiempo. Para Miguel Aguiló “los puentes … expresan la superación de un obstáculo, de una incomunicación, de una situación comprometida”. Es el afán sempiterno por vencer los límites que amordazan la voluntad humana.

El puente es la metáfora perfecta de la unión entre las partes, de la comunicación, del intercambio y del progreso. También significa el paso o tránsito hacia el otro lado, hacia lo desconocido, con toda la carga de magia y misterio que lo rodea. Es la victoria de la razón sobre las fuerzas de la Naturaleza, aunque para otros es fruto de la intervención del maligno. Fernández-Troyano nos recuerda que la magia consiste en “sostener el camino en el aire”, dejándolo flotar contra todo pronóstico, sorteando el orden establecido.

Es un símbolo de poder para quien lo controla y un paso hacia la inmortalidad para quien lo construye. Para otros es propaganda, una “golosina visual”, una marca o un reclamo turístico. Sin embargo, para los ingenieros, un puente puede ser la más bella obra que la razón ha regalado a los humanos. Aprender a ver un puente, por tanto, va más allá de la simple contemplación; consiste en descubrir su verdad interna, aquello que el autor ha querido expresar y que, en esencia, es la posibilidad de crear una estructura sólida, bella y funcional, como diría Vitruvio.

*Puente della Trinitá* en Florencia. Imagen: © V. Yepes

Para José Antonio Fernández-Ordoñez el paradigma vitruviano queda limitado en nuestra búsqueda de entender el lenguaje del puente, incluso si se añaden las componentes constructivas y económicas. En efecto, tal y como nos refiere él mismo, le “interesan especialmente otros tres aspectos menos tratados, pero no menos importantes, como son el estético, el histórico y el de integración con su entorno, es decir, la naturaleza”.

Un puente es una obra de arte que, más allá de su arquitectura, presenta una dialéctica tensional que, bien entendida e interpretada, permite escucharla como una composición musical, con todos sus matices, timbres y tonos. Sin embargo, como cualquier obra de arte, es imposible descifrarla fuera de contexto, sin su entorno, sin la sociedad que la creó. Un puente genera, por tanto, otra dialéctica, la visual con el paisaje, creando o destruyendo el lugar, lo cual implica que el puente debe ser algo singular, creado “ad hoc”, que no sirve para cualquier sitio o circunstancia, y que debe ser fruto de la sociedad que lo ha visto nacer. Santiago Hernández (2009:11) expresa claramente esta idea cuando habla del “alma de los puentes”, es decir, “de la capacidad de provocar sentimientos en quienes los han construido y en aquellos que, cuando los contemplan, pueden ver a todos quienes han hecho posible que su obra sirva a miles de personas durante siglos. El puente es más que un libro, más que una película, más que un relato, más que una herramienta… el puente nos permite vivir una ‘experiencia’ que nos une a su origen, su pasado, su presente y su futuro”.

El protagonista, por tanto, es ese lenguaje dialéctico, interno del puente y externo con el contexto y el paisaje. Cuando el propio puente, su autor o su promotor prevalecen deliberadamente sobre este lenguaje, el puente pierde gran parte de su valor, prostituyendo su esencia. A este respecto, Miguel Aguiló ya nos previene de estos peligros: “… lo puramente funcional va siempre acompañado de intenciones simbólicas, de emulación, de prestigio o de ostentación, y son precisamente estas finalidades no explícitas en la función las que fomentan o impulsan la desproporción”. Es quizás en este contexto cuando ciertas reflexiones de Florentino Regalado pueden adquirir mayor brillo: “una reflexión meticulosa, la reflexión y el sentido común, y unas ciertas dosis de humildad, se echan a faltar en lo que se proyecta y construye”.

Quizá Steinman y Watson fueron capaces de sintetizar lo que el puente significa para aquellos que los amamos profundamente, “porque un puente es algo más que una cosa de acero y piedra: es la concreción del esfuerzo de cabezas, corazones y manos humanas. Un puente es más que una suma de deformaciones y tensiones: es una expresión del impulso de los hombres —un desafío y una oportunidad de crear belleza—. Un puente es el símbolo del heroico esfuerzo de la humanidad hacia el dominio de las fuerzas de la naturaleza. Un puente es un monumento a la tenaz voluntad de conquista del género humano”.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Notas sobre los puentes renacentistas

Vamos a intentar divulgar, en unas breves notas, algunas ideas sobre los puentes renacentistas. Este post sigue a otros anteriores que trataron sobre la ingeniería en el Renacimiento, el diseño de los arcos a lo largo de la historia o el concepto de puente. Espero que os guste, a sabiendas de que me dejaré muchísimas cosas por el camino.

Empecemos, pues. El Renacimiento imprime a todas las ramas del saber un impulso renovador aún no extinguido. A lo largo los siglos XV y XVI empieza a cambiar la profesión que desembocará en el ingeniero. Las cortes europeas exigen profesionales que se ocupen más allá de las máquinas de guerra y se ocupen de la dirección de proyectos técnicos como los caminos, los puentes, las obras hidráulicas, etc. Además, se da un fuerte impulso hacia la creación de un soporte científico que avale la ingeniería: “ars sine scientia nihil est”, cita, por cierto, del arquitecto Jean Mignot. De hecho, los ingenieros del Renacimiento juzgan fundamental la asociación de su profesión con las matemáticas (Millán, 2004). Un hito fundamental fue el tratado de Leon Battista Alberti, De reaedificatoria, escrita en latín entre 1443 y 1452, que pretende imitar y culminar la obra de Vitruvio. El trabajo de Alberti se publicó en 1485, y un año después el de Vitruvio, en aquellos primeros años de la imprenta. Leonardo da Vinci (1452-1519) empezó a formular los principios de la naciente teoría estructural y Andrea Palladio (1518-1580) introdujo el concepto de cercha o entramado. Sin embargo, hay que esperar al siglo XVII para encontrarnos con las figuras de Galileo, Hooke o Mariotte para empezar a cimentar la teoría de las estructuras que se desarrollaría en los siglos posteriores.

La ingeniería de corte típicamente medieval cambió en la Italia del siglo XV (García-Tapia, 1987). En España este cambio de mentalidad fue más tardío, no pudiéndose hablar con propiedad de una ingeniería clasicista hasta la segunda mitad del siglo XVI, con la aparición de los ingenieros teóricos y de los arquitectos-ingenieros. Sin embargo, las circunstancias históricas y sociales del siglo XVII abortaron tempranamente este Renacimiento en la ingeniería. Las numerosas obras locales emprendidas entonces estuvieron a cargo de maestros de obras que difícilmente podrían catalogarse como ingenieros en el sentido actual.

El descubrimiento de las ruinas clásicas romanas, olvidadas en el Medievo, y el hallazgo, por el estudioso Poggio Bracciolini, de un manuscrito de Vitruvio en la biblioteca del monasterio de San Gall en el año 1415 marcan, según García-Tapia (1987) los dos acontecimientos que contribuyeron a la ingeniería del Renacimiento. Fue la invención de la imprenta la que catapultó la difusión del libro de Vitruvio. En él se definía el ideal de arquitecto-ingeniero humanista, con conocimientos en diversas artes, además de definir los procedimientos constructivos de la antigüedad clásica y los tipos de máquina empleados por los romanos del siglo I. García-Tapia (1987:25) describe instrumentos, ingenios y máquinas empleados en las obras públicas renacentistas.

Las técnicas constructivas de los siglos XV y XVI no cambian sustancialmente respecto a las empleadas en la Baja Edad Media. Sin embargo, la estética cambia completamente, volviéndose a las formas regulares de la época clásica. Así, los arcos de medio punto vuelven a utilizarse en los puentes, siendo ejemplos canónicos los de Rialto en Venecia (1590), Pont Neuf de París (1578-1604), o el Puente della Trinitá en Florencia (1570). La consideración renacentista del puente como obra de arte se tradujo en una mayor decoración y en la incorporación de esculturas, en una búsqueda por el equilibrio y elegancia de las formas.

Puente de Rialto (Venecia). Fotografía de Rüdiger Wölk.

Los transportes con carruajes se desarrollaron tras la Edad Media, lo cual implicó la desaparición de los incómodos puentes apuntados posteriores al siglo XV y la aparición de bóvedas rebajadas. Sin embargo, el rebajamiento aumentaba los empujes sobre las pilas, lo que obligaba a aumentar la prudencia durante la construcción. Se empezaron a utilizar con frecuencia arcos segmentales y a líneas “anse de panier” (arco de varios centros). El más atrevido fue el Puente della Trinitá en Florencia, con un rebajamiento de 1/7 que no volvió a repetirse hasta el siglo XVIII (Grattesat, 1981).

Ponte Vecchio (Florencia). Imagen: V. Yepes(c)

El Renacimiento irrumpió en el mundo de la ingeniería de los puentes con un precedente excepcional, ciertamente anacrónico, rompedor con la tipología de los puentes medievales del momento. Se trata del Ponte Vecchio, construido en Florencia en 1345, obra de Tadeo Gaddi.

Los puentes españoles de la segunda mitad del siglo XVI, presentan, según indica González Tascón (2008), cierto arcaísmo que se manifiesta en el diseño de los tajamares y espolones, que frecuentemente llegan hasta la calzada en forma de apartaderos. Esto se debe, en parte, a que los maestros canteros se habían curtido en la reparación de puentes romanos y medievales. Ejemplos de este tipo de puentes se pueden encontrar en los de Almaraz o Montoro. Sin embargo, las nuevas tendencias europeas evitan este diseño pesado, como es el caso del puente de Segovia (Madrid), diseñado en parte por Juan de Herrera, o el de Ariza en Úbeda (Jaén), obra de Andrés de Vandelvira.

No me quiero despedir sin hablar, aunque sea un poco, del puente de Segovia de Madrid, aunque sea como pequeño homenaje a Juan de Herrera y el Renacimiento español. Una provisión de Felipe II en el año 1574 da inicio en Madrid, sobre el Manzanares, el puente de Segovia, cuyas obras concluyeron en 1584. La estructura superaba el ámbito local para agrupar el tráfico proveniente de Castilla, por un lado, y de Toledo, Andalucía y Extremadura. El proyecto inicial fue del Maestro Mayor de Obras, Gaspar de la Vega, con arcos decrecientes y perfil medieval en lomo de asno. Sin embargo, cuando a la muerte del primero se hizo cargo Juan de Herrera de la obra, con los encepados de los cimientos ya construidos, decide una rasante horizontal conseguida al recrecer los tímpanos sobre los arcos laterales. De esta forma resultaba innecesario el crecimiento de las luces de los arcos extremos hacia el centro, dándole una impronta moderna al puente. Se trata, por tanto, de un puente de fábrica de sillería con 9 bóvedas de cañón, de una luz entre 9,4 y 12 m, con espesores de pilas entre 5 y 6,7 m. La longitud total es de 185 m y la anchura original del tablero de 12 m. La máxima altura sobre la rasante es de 11,4 m. Se proyectaron tajamares triangulares aguas arriba y semicirculares aguas abajo, rematándose con sombreretes que alcanzan la cota correspondiente al trasdós de la clave de los arcos. En palabras de Arenas (2002) “el puente de Herrera es, más que un puente, una masa ordenada de piedra granítica, …, cuyas formas y proporciones transmiten una imagen de serenidad y equilibrio tan logrados que resulta, en su tremenda austeridad granítica, de una belleza innegable”.

Referencias:

ARENAS, J.J. (2002). Caminos en el aire: los puentes. Colección ciencias, humanidades e ingeniería. Ed. Colegio de Ingenieros de Caminos, Canales y Puertos, Madrid.

GARCÍA TAPIA, N. (1987). Ingeniería civil española en el Renacimiento, en Cuatro conferencias sobre historia de la ingeniería de obras públicas en España. CEDEX, Madrid, pp. 7-42.

GONZÁLEZ-TASCÓN, I. (2008). Las vías terrestres y marítimas en la España medieval, en: Ministerio de Fomento, Ars Mechanicae, Ingeniería medieval en España, pp. 21-67.

MILLÁN, A. (2004). Leon Battista Alberti, la ingeniería y las matemáticas del Renacimiento. Suma, 47:93-97.

YEPES, V. (2010). Puentes históricos sobre el viejo cauce del Turia. Un análisis histórico, estético y constructivo a las obras de fábrica. Universitat Politècnica de València. Inédito.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Valoración de la contribución de una infraestructura a la sostenibilidad social bajo condiciones de incertidumbre

Nos acaban de publicar en la revista de Elsevier del primer cuartil, Environmental Impact Assessment Review, un artículo donde se valora la contribución de una infraestructura a la sostenibilidad social bajo condiciones de incertidumbre. Este artículo forma parte de nuestra línea de investigación BRIDLIFE en la que se pretenden optimizar estructuras atendiendo no solo a su coste, sino al impacto ambiental y social que generan a lo largo de su ciclo de vida.

Abstract:

Assessing the viability of a public infrastructure includes economic, technical and environmental aspects; however, on many occasions, the social aspects are not always adequately considered. This article proposes a procedure to estimate the social sustainability of infrastructure projects under conditions of uncertainty, based on a multicriteria deterministic method. The variability of the method inputs is contributed by the decision-makers. Uncertain inputs are treated through uniform and beta PERT distributions. The Monte Carlo method is used to propagate uncertainty in the method. A road infrastructure improvement case study in El Salvador illustrates this treatment. The main results determine the variability of the short and long-term social improvement indices by infrastructure and the probability of the position in prioritizing the alternatives. The proposed mechanism improves the reliability of the decision-making early in infrastructure projects, taking their social contribution into account. The results can complement environmental and economic sustainability assessments.

Keywords:

Infrastructure;
Multicriteria decision-making;
Uncertainty;
Social sustainability

Reference:

SIERRA, L.A.; YEPES, V.; PELLICER, E. (2017). Assessing the social sustainability contribution of an infrastructure project under conditions of uncertainty. Environmental Impact Assessment Review,67:61-72.

Construcción de puentes arco por voladizos sucesivos atirantados con torre provisional

Se pueden construir puentes arco por voladizos sucesivos, sujetando cada tramo mediante tirantes desde torres provisionales. Una vez se tocan los semiarcos, se puede eliminar el atirantamiento y las torres y construir sobre el arco las pilas y el tablero. Es una técnica similar al avance por voladizos sucesivos de los tableros rectos, pudiéndose realizar con dovelas prefabricadas o bien por carro de avance hormigonando “in situ”. Este procedimiento constructivo permite la construcción de arcos de grandes luces, empleando un volumen de medios auxiliares reducido en comparación con otros métodos.

Este procedimiento constructivo se empleó en el montaje de cimbras, aunque hasta finales del siglo XIX no se empezó a utilizar para construir un arco completo. En efecto, James B. Eads construyó el puente metálico de San Luis (1867-1874) sobre el Mississippi con atirantamientos provisionales. El sistema también lo utilizó Gustave Eiffel en la construcción de los puentes arco metálicos de María Pía y Garabit.

Construcción del puente María Pía (Oporto). Gustave Eiffel y Théophile Seyring proyectaron este puente, que con 160 m de luz principal, fue el arco más largo del mundo entre 1877, fecha de su terminación, y 1884.

Viaducto de Garabit , sobre el río Truyère (Francia). Con sus 165 m de luz principal, fue el mayor arco desde 1884 a 1886. El puente lo construyó la compañía de Eiffel.

La técnica empezó a usarse en arcos de hormigón en 1952, cuando Freyssinet empleó parcialmente este método en los arranques de los arcos en los viaductos de la carretera al puerto de La Guaira, en Caracas. El tramo central de la cimbra se elevó desde el fondo del barranco, apoyándose en los arranques de arco atirantados.

Construcción del Viaducto 1 de la autopista Caracas, la Guaira (Venezuela). Los viaductos, construidos en 1952, son tres puentes arco biarticulados de 152, 146 y 138 m de luz, de E. Freyssinet.

Una realización más reciente construida con este sistema de atirantamiento provisional es el puente arco de ferrocarril sobre el embalse de Contreras en la línea de alta velocidad Madrid-Levante (Manterola et al., 2012). Se trata de un arco de 261 m de luz, con tablero superior de hormigón pretensado y una longitud total de 587, 25 m. Los semiarcos avanzan por voladizos sucesivos mediante hormigonado con carro de avance, para lo cual se disponen dos pilonos metálicos sobre el tablero, en la vertical de unas pilas provisionales.

Puente de ferrocarril sobre el embalse de Contreras. Detalle de la construcción del arco.

A continuación os dejo algunos vídeos que muestran la construcción del viaducto de Contreras. Espero que os sean de interés.

Referencia:

MANTEROLA, J.; MARTÍNEZ, A.; NAVARRO, J.A.; MARTÍN, B. (2012). Puente arco de ferrocarril sobre el embalse de Contreras en la línea de alta velocidad Madrid-Levante. Hormigón y Acero, 63:5-29.

Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.

Ejecución de una losa postesada en edificación

Los forjados de losa postesa o forjados postensados son forjados que han sido elaborados mediante la técnica de tesar cables de acero (armadura activa), después del fraguado del hormigón y cuando este ha alcanzado una resistencia suficiente para soportar las tensiones provocadas por dicho tesado. Se requieren hormigones y aceros de alta resistencia. Como consecuencia del trazado curvo de los tendones también aparecen fuerzas de desviación que pueden llegar a equilibrar el peso propio de la estructura, las cargas muertas e incluso parte de las sobrecargas. Existen dos variantes de la técnica: armadura postesa adherente y armadura postesa no adherente. Para forjados de edificación se suelen emplear armadura no adherente, por lo estricto de los cantos y por la facilidad de montaje. Este tipo de losas se utilizan en estructuras de edificios en altura, estructuras por debajo de la cota de rasante, cimentaciones por losa, parkings, puentes, depósitos, estructuras de edificaciones industriales, etc.

Algunas de las ventajas del uso de estos sistemas son las siguientes:

Reducción de los materiales de construcción (hasta un 40% de hormigón y un 75% de acero).
La reducción de peso de la estructura permite reducir el espesor y el armado de la losa de cimentación.
Aumento de altura libre entre plantas al reducir a la mitad el canto de la losa comparado con un forjado tradicional.
Continuidad estructural que permite un menor número de juntas de hormigonado y dilatación, así como una mayor integridad estructural.
Reducción considerable del número de pilares y aumento de los vanos.
Evita la aparición de fisuras y es impermeable al estar el hormigón comprimido.

A continuación os dejo algunos vídeos explicativos.

Optimización heurística de ménsulas cortas mediante elementos finitos con fisuración distribuida

A continuación os dejo un artículo donde se aplica la optimización heurística mediante recocido simulado de ménsulas cortas de hormigón armado, usando para ello elementos finitos con fisuración distribuida.

También puedes encontrar el artículo en acceso abierto en: https://www.witpress.com/elibrary/wit-transactions-on-the-built-environment/125/23501

Referencia:

ROJAS, G.; ROJAS, P.; GONZÁLEZ-VIDOSA, F.; YEPES, V. (2012). Heuristic optimization of short corbels by smeared cracking finite element analysis. International Conference on Computer Aided Optimum Design in Engineering, 20-22 june. Computer Aided Optimum Design in Engineering XII. Vol. 125, pp. 71-82. Edited By: S. HERNANDEZ, University of A Coruña, Spain, C.A. BREBBIA, Wessex Institute of Technology, UK and W.P. DE WILDE, Vrije Universiteit Brussel, Belgium. DOI: 10.2495/OP120071 ISSN: 1743-3509 (on line).

Descargar (PDF, 486KB)