A veces la Naturaleza nos sorprende cada día más. ¿Es posible que el comportamiento de las hormigas nos ayude a optimizar estructuras complejas, como, por ejemplo, un puente? Pues vamos a ver que sí. Este artículo es una continuación de otros artículos en los que hablamos de la posibilidad de optimizar estructuras de hormigón. La optimización por colonia de hormigas (ant colony optimization) será una metaheurística que nos permitirá realizar este tipo de operaciones. A continuación vamos a contar los fundamentos básicos y en las referencias os dejo, incluso, algunos artículos donde hemos podido utilizar esta técnica de forma exitosa.
Colorni, Dorigo y Maniezzo (1991) sugirieron la idea de imitar el comportamiento de los insectos para encontrar soluciones a los problemas de optimización combinatoria. El principio de la metaheurística denominada “Ant System Optimization, ACO” se basa en el comportamiento colectivo de las hormigas en la búsqueda de alimentos para su subsistencia, capaces de encontrar el camino más corto entre una fuente de comida y su hormiguero.
Primero, las hormigas exploran el entorno de su hormiguero de forma aleatoria. Tan pronto como un individuo encuentra una fuente de comida, evalúa su cantidad y calidad y transporta un poco al hormiguero. Durante el regreso, la hormiga deja por el camino una señal odorífera, depositando una sustancia denominada feromona, para que las demás hormigas puedan seguirla. Después de un tiempo, el camino hacia el alimento se indicará por un rastro oloroso que crece con el número de hormigas que lo recorren y desaparece en caso contrario. El resultado final es la optimización del trabajo de todo el hormiguero en su búsqueda de comida.
En la Figura se muestra cómo las hormigas encuentran el camino más corto. En a) las hormigas deben decidir un camino; en b) se toma uno al azar; en c) dado que la velocidad de una hormiga se considera aproximadamente constante, las que llegan antes vuelven eligiendo el camino con mayor acumulación de feromona. En d), se circula por el camino más corto, desapareciendo por evaporación el rastro en el más largo.
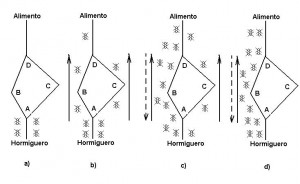
La analogía con una metaheurística de optimización puede establecerse de la siguiente forma:
- La búsqueda de alimento por las hormigas es equivalente a la exploración de soluciones factibles a un problema combinatorio.
- La cantidad de alimento hallada en un lugar es similar al valor de la función objetivo.
- El rastro de feromona es la memoria adaptativa del método.
Un esquema básico de la metaheurística sería el siguiente:
- Iniciar un rastro de feromona.
- Mientras no se encuentre un criterio de parada:
- Para cada hormiga artificial, construir una nueva solución a partir del rastro actual y evaluarla.
- Actualizar el rastro de feromona.
El componente más importante de un sistema de hormigas es la gestión de las huellas olfativas. En su versión estándar, los rastros se usan en relación con la función objetivo para construir nuevas soluciones. Una vez se ha construido, éstos se actualizan de la siguiente forma: primero todos los rastros se debilitan para simular la evaporación del feronoma; después aquellos que corresponden a los elementos que se han empleado para la construcción, se refuerzan teniendo en cuenta la calidad de la solución.
El siguiente vídeo puede ayudaros a comprender el comportamiento de las hormigas. Espero que os guste.
Referencias:
COLORNI, A.; DORIGO, M.; MANIEZZO, V. (1991). Distributed optimization by ant colonies, in VARELA, F.J.; BOURGINE, P. (eds.) Proceedings of the First European Conference on Artificial Life (ECAL-91). The MIT Press: Cambrige, MA, 134-142.
MARTÍNEZ, F.J.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A.; ALCALÁ, J. (2011). Design of tall bridge piers by ant colony optimization. Engineering Structures, 33:2320-2329.
MARTÍNEZ, F.J.; GONZÁLEZ-VIDOSA, F.; HOSPITALER, A.; YEPES, V. (2010). Heuristic Optimization of RC Bridge Piers with Rectangular Hollow Sections. Computers & Structures, 88: 375-386. ISSN: 0045-7949. (link)
YEPES, V. (2003). Apuntes de optimización heurística en ingeniería. Editorial de la Universidad Politécnica de Valencia. Ref. 2003.249. Valencia, 266 pp. Depósito legal: V-2720-2003.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional.